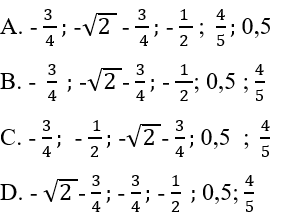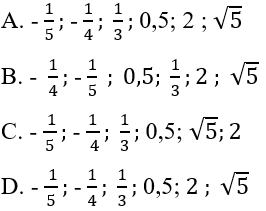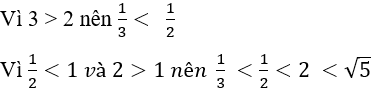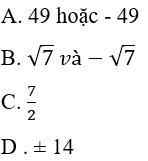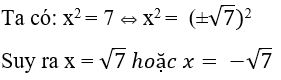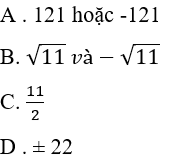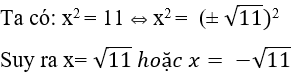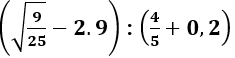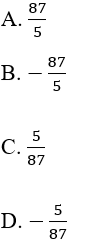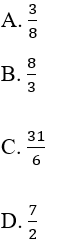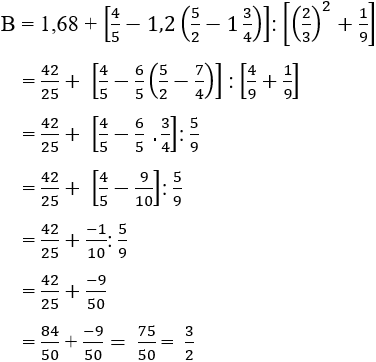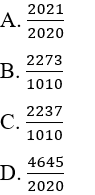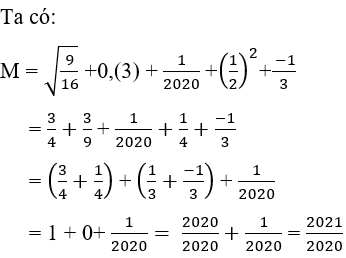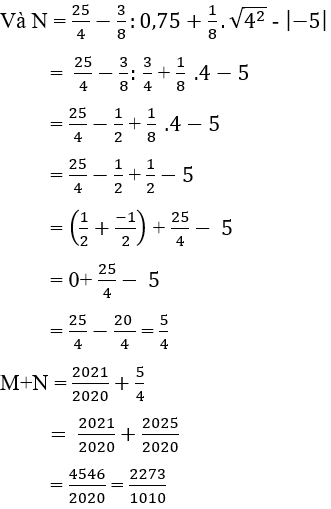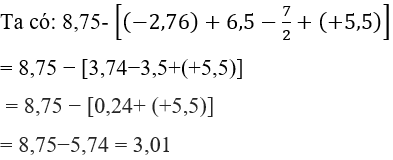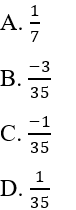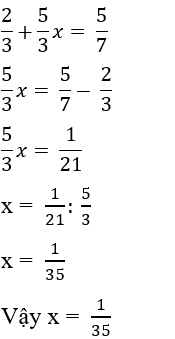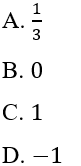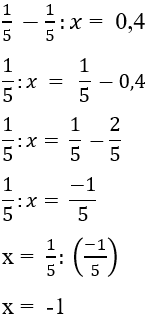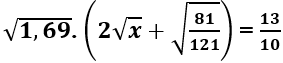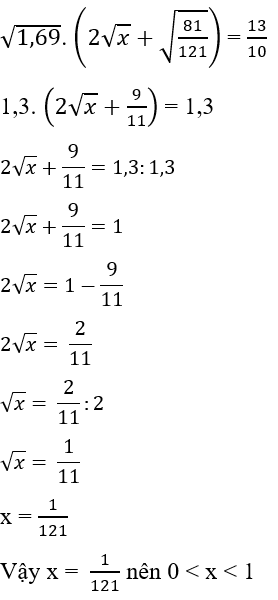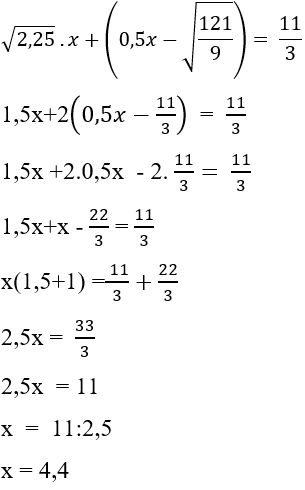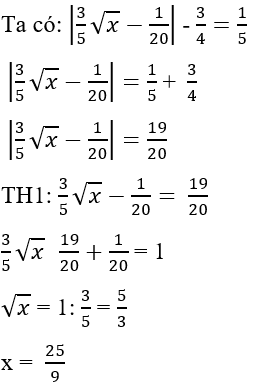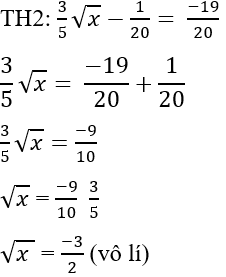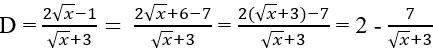Số thực là gì? Bài tập vận dụng về số thực

Cô Nguyễn Thanh Phương 08/07/2023

Mời các em theo dõi nội dung bài học về Số thực là gì? Bài tập vận dụng về số thực do thầy cô trường THCS Bình Chánh biên soạn. Hy vọng sẽ là tài liệu hữu ích giúp các em học tốt và hoàn thành tốt bài tập của mình.

Mục lục

Số thực là gì?

Số thực là số được định nghĩa bởi các thành phần của chính nó. Trong đó tập hợp số thực được xem như là hợp của tập hợp các số vô tỉ với tập hợp các số hữu tỉ. Số thực này có thể là đại số hoặc số siêu việt. Tập hợp số thực được đặt làm đối trọng với tập hợp của số phức. Số thực được mô tả một cách không chính thức theo nhiều cách. Số thực thường sẽ bao gồm cả số dương, số 0 và số âm.

R là tập hợp số gì?

Trong toán học, R là ký hiệu của tập số thực. Đây là tập hợp của cả số hữu tỉ và vô tỉ. R chính là tập số lớn nhất trên tập số.

Bạn đang xem: Số thực là gì? Bài tập vận dụng về số thực

Tập hợp số tự nhiên N = {0, 1, 2,…}, tập số nguyên Z = {…-3, -2, -1, 0, 1, 2,…}…tất cả các tập số này đều là tập con của R. Và cả số vô tỉ như II = 3,144592 hay = 1,414214….Tất cả các số ta đã biết đều thuộc R.

Tập hợp số thực có kí hiệu là gì?

Tập hợp số thực có ký hiệu là: R (R = Q U I)

Trong đó:

N là tập hợp số tự nhiên
Z là tập hợp số nguyên
Q là tập hợp số hữu tỉ
I = RQ tập hợp số vô tỉ.

Mỗi một số thực được biểu diễn bởi một điểm trên trục số. Và ngược lại, mỗi điểm trên trục số sẽ biểu diễn một số thực. Chỉ có tập hợp số thực thì mới có thể lấp đầy trục số.

Trong tập hợp R, ta cũng có thể định nghĩa các phép toán cộng, trừ, nhân, chia, lũy thừa,…và trong các phép toán các số thực cũng có các tính chất như phép toán trong tập hợp các số hữu tỉ.

Tính chất của số thực R

Bất kỳ số thực khác không là số âm hoặc số dương
Tổng hay tích của 2 số thực không âm là một số thực không âm
Số thực là tập hợp vô hạn, có thể đếm được của các số thực
Có hệ thống các tập hợp con vô hạn có thể đếm được của các số thực
Số thực có thể được sử dụng để thể hiện các phép đo đại lượng liên tục
Số thực có thể biểu thị bằng biểu diễn thập phân.

Ví dụ về số thực R trong toán học

Tập hợp R là ký hiệu của tập hợp số thực, bao gồm số hữu tỉ và số vô tỉ

Ví dụ

Số nguyên là -5, 2, 3, -8,…

Phân số là $\frac{4}{3};\frac{8}{5}$

R là gì trong hình học?

Không chỉ là một ký hiệu trong đại số, R còn được sử dụng trong hình học, R đôi khi được sử dụng để thể hiện bán kính của đường tròn nội tiếp tam giác. Đặc biệt r còn được sử dụng trong công thức tính chu vi của diện tích hình tròn:

Chu vi: C = dII = 2r.II

Diện tích: S= πR²

Các dạng bài tập thường gặp về số thực và hướng dẫn cách giải

Dạng 1: Các câu hỏi về bài tập hợp số

Hướng dẫn giải:

Lưu ý các ký hiệu về tập hợp số:

+ N: Tập hợp các số tự nhiên

+ Z: Tập hợp các số nguyên

+ Q: Tập hợp các số hữu tỉ

+ I: là tập hợp các số vô tỉ

+ R: là tập hợp các số thực.

Ta có quan hệ giữa các tập hợp số như sau: N ⊂ Z ⊂ Q ⊂ R; I ⊂ R.

Dạng 2: là tìm số chưa biết trong một đẳng thức

Hướng dẫn giải:

+ Sử dụng từ tính chất của các phép toán

+ Sử dụng quan hệ giữa các số hạng trong một tổng và một hiệu. Quan hệ giữa các thừa số trong một tích, quan hệ giữa số bị chia, số chia và thương của phép chia.

+ Sử dụng đến quy tắc chuyển vế, phá ngoặc.

Dạng 3: Tính giá trị của biểu thức nào đó

Hướng dẫn giải:

+ Thực hiện phối hợp các phép tính cộng, trừ, nhân, chia và lũy thừa. Tuy nhiên, bạn cần chú ý đến thứ tự thực hiện.

+ Rút gọn các phân số khi cần thiết

+ Chú ý để vận dụng các tính chất của phép toán sao cho thích hợp.

Dạng 4: So sánh các số thực:

Hướng dẫn giải:

Để giải dạng bài tập này cần phải nắm chắc kiến thức dưới đây:

– Với hai số thực x và y bất kì, ta sẽ có như sau: x = y hoặc x < y hoặc x > y.

– Với các số thực lớn hơn số 0 thì được gọi là số thực dương và ngược lại, các số thực nhỏ hơn số 0 thì được gọi là số thực âm.

– Số 0 không phải là số thực dương cũng không là số thực âm.

– Khi so sánh các số thực dương cũng là tương tự như khi so sánh các số hữu tỉ.

– Với hai số a và b là hai số thực dương, điều kiện nếu a > b thì √a > √b.

Ví dụ: Cho các số thực sau: -11; 3, -1,5; 6; 6,5 . Hãy sắp xếp các số thực này theo thứ tự từ lớn đến nhỏ.

Hướng dẫn giải:

Sắp xếp các số thực trên theo thứ tự từ lớn đến nhỏ là:

6,5 > 6 > 3 > -1,5 > -10.

Các dạng bài tập thường gặp về số thực và hướng dẫn cách giải

Bài tập trắc nghiệm số thực có đáp án

Câu 1: Phát biểu nào sau đây là đúng?

A. Số nguyên không phải số thực

B. Phân số không phải số thực

C. Số vô tỉ không phải số thực

D. Cả ba loại số trên đều là số thực

Lời giải:

Ta thấy số nguyên, phân số hay số vô tỉ đều là số thực

Đáp án cần chọn là: D

Câu 2: Chọn câu đúng nhất:

A. R = I ∪ Q

B. I ⊂ R

C. I ∩ Q = ∅

D. Cả A, B, C đều đúng

Lời giải:

Số thực bao gồm số hữu tỉ và số vô tỉ nên R = I ∪ Q từ đó suy ra I ⊂ R.

Ta có:

– Mỗi số hữu tỉ được biểu diễn bởi một số thập phân hữu hạn tuần hoàn hoặc vô hạn tuần hoàn.

– Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn.

Suy ra I ∩ Q = ∅

Do đó cả A, B, C đều đúng.

Đáp án cần chọn là: D

Câu 3: Phát biểu nào sau đây là sai?

A. Mọi số vô tỉ đều là số thực

B. Mọi số thực đều là số vô tỉ

C. Mỗi số nguyên đều là số hữu tỉ

D. Số 0 là số hữu tỉ cũng là số thực.

Lời giải:

Số thực bao gồm số hữu tỉ và số vô tỉ. Tuy nhiên nếu số thực mà là số hữu tỉ thì sẽ khác số vô tỉ. Do đó phát biểu mọi số thực đều là số vô tỉ là sai.

Đáp án cần chọn là: B

Câu 4: R ∩ I =

A. R

B. Q

C. ∅

D. I

Lời giải:

Do R = I ∪ Q do đó R ∩ I = I

Đáp án cần chọn là: D

Câu 5: R ∩ Q =

A. R

B. Q

C. ∅

D. I

Lời giải:

Do R = I ∪ Q suy ra R ∩ Q = Q.

Đáp án cần chọn là: B

Câu 6: Chọn chữ số thích hợp điền vào chỗ trống -5,07 < -5,…4

A. 1 ; 2 ; …9

B. 0 ;1 ; 2 ; …9

C. 0

D. 0 ; 1

Lời giải:

Áp dụng so sánh hai số nguyên âm ta thấy chỉ có −5,07 < −5,04. Do đó ô trống cần điền là số 0

Đáp án cần chọn là: C

Câu 7: Chọn chữ số thích hợp điền vào chỗ trống -11,29 < – 11,…9

A. 1 ; 2; …9

B. 3

C. ∅

D. 0 ; 1

Lời giải:

Áp dụng so sánh hai số nguyên âm ta thấy −11,29 < −11,09 và −11,29 < −11,19. Do đó ô trống cần điền có thể là số 0 hoặc 11.

Đáp án cần chọn là: D

Câu 8: Sắp xếp các số sau theo thứ tự tăng dần:

Lời giải:

Ta chia các số đã cho làm 2 nhóm

Nhóm 1: vì

Lại có nên

Nhóm 2:

Vậy ta có dãy số tăng dần là

Đáp án cần chọn là: D

Câu 9: Sắp xếp các số sau theo thứ tự tăng dần:

Lời giải:

Ta chia các số đã cho thành hai nhóm

Nhóm 1: vì 5 > 4 nên

Nhóm 2 Ta có: 0,5 = 1/2

Vậy ta có dãy số tăng dần là:

Đáp án cần chọn là: D

Câu 10: Nếu x²= 7 thì x bằng:

Lời giải:

Đáp án cần chọn là: B

Câu 11: Nếu x²= 11 thì x bằng:

Lời giải:

Đáp án cần chọn là: B

Câu 12: Kết quả của phép tính

Lời giải:

/p>

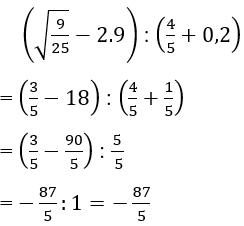
Đáp án cần chọn là: B

Câu 13: Kết quả của phép tính 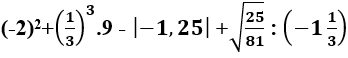là:

Lời giải:

Đáp án cần chọn là: B

Câu 14: Cho 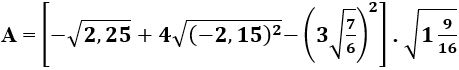và . So sánh A và B

A. A > B

B. A < B

C. A = B

D. A ≥ B

Lời giải:

Ta có:

Và

Từ đó A < B

Đáp án cần chọn là: B

Câu 15: Cho 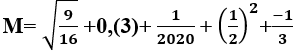và . Tính M + N

Lời giải:

Đáp án cần chọn là: B

Câu 16: Gía trị nào sau đây là kết quả của phép tính: (-45,7) + [(+5,7) + (+5,75) + (-0,75)]

Lời giải:

(−45,7 ) + [(+5,7) + (+5,75) + (−0,75)]

= (−45,7) + (5,7+5,75−0,75) = −45,7+5,7+5 = −40+5 = −35

Đáp án cần chọn là: B

Câu 17: Giá trị nào sau đây là kết quả của phép tính:

A. 30,1

B. 3,01

C. 3,10

D. 3,11

Lời giải:

Đáp án cần chọn là: B

Câu 18: Tìm x biết

Lời giải:

Đáp án cần chọn là: D

Câu 19: Tìm x biết

Lời giải:

Đáp án cần chọn là: D

Câu 20: Gọi x là giá trị thỏa mãn

A. x > 2

B. x < 0

C. 0 < x < 1

D. x > 3

Lời giải:

Ta có:

Đáp án cần chọn là: C

Câu 21: Gọi x là giá trị thỏa mãn 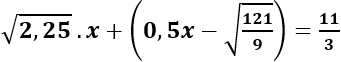. Chọn câu đúng.

A. x > 5

B. x < 4

C. 4 < x < 5

D. x = 4

Lời giải:

Đáp án cần chọn là: C

Câu 22: Có bao nhiêu giá trị của x thỏa mãn

A. 1

B. 2

C. 3

D. 0

Lời giải:

Vậy có một giá trị của x thỏa mãn là x =

Đáp án cần chọn là: A

Câu 23: Có bao nhiêu giá trị của x thỏa mãn

A. 1

B. 2

C. 3

D. 0

Lời giải:

Vì với mọi x ≥ 0 nên không có giá trị nào của x thỏa mãn yêu cầu bài toán

Đáp án cần chọn là: C

Câu 24: Gía trị nào của x thỏa mãn [(7+0,004x):0,9]: 24,7-12,3 = 77,7

A. x = 49842

B. x = 498

C. x = 498420

D. x =498425

Lời giải:

[(7+0,004x) : 0,9] : 24,7−12,3 = 77,7

[(7+0,004x):0,9] : 24,7 = 77,7+12,3

[(7+0,004x):0,9] : 24,7 =90

(7+0,004x) : 0,9 = 90.24,7

(7+0,004x) : 0,9 = 2223

7+0,004x = 2223.0,9

7+0,004x = 2000,7

0,004x = 1993,7

x = 498425

Vậy x = 498425

Đáp án cần chọn là: D

Câu 25: Giá trị nào của x thỏa mãn (10,22:0,7)x : 0,001 – = 12,2

A, x = 0,1

B. x = 0,0001

C. x = 0,01

D. x = 0,001

Lời giải:

(10,22:0,7)x:0,001 – = 12,2

14,6x:0,001−2,4 = 12,2

14,6x:0,001 = 12,2+2,4

14,6x:0,001 = 14,6

14,6x = 14,6.0,001

x = 0,001

Đáp án cần chọn là: D

Câu 26: Tìm số tự nhiên x để D = có giá trị là một số nguyên

A. x = 4

B. x = 16

C. x = 9

D. x = 10

Lời giải:

Ta có:

Để D ∈ Z thì (√x + 2) phải thuộc Z và là ước của 5.

Vì (√x + 2) > 0 nên chỉ có hai trường hợp:

Trường hợp 1: √x + 2 = 1 ⇔ √x = −1 (vô lý)

Trường hợp 2: √x + 2 = 5 ⇔ √x = 3 ⇔ x = 9 (thỏa mãn).

Vậy để D ∈ Z thì x = 9 (khi đó D = 0).

Đáp án cần chọn là: C

Câu 27: Tìm số tự nhiên x để D = có giá trị là một số nguyên

A. x = 4

B. x = 16

C. x = 9

D. x = 10

Lời giải:

Ta có:

Để D ∈ Z thì ∈ Z do đó √x + 3 là ước của 7.

Vì (√x + 3) > 0 nên chỉ có hai trường hợp

Trường hợp 1: √x + 3 = 1 ⇔ √x = −2 (vô lý)

Trường hợp 1: √x + 3 = 7 ⇔ √x = 4 ⇔ x = 16 (thỏa mãn).

Vậy x = 16 thì D ∈ Z (khi đó D = 1).

Đáp án cần chọn là: B

***

Trên đây là nội dung bài học Số thực là gì? Bài tập vận dụng về số thực do thầy cô trường THCS Bình Chánh biên soạn và tổng hợp. Hy vọng sẽ giúp các em hiểu rõ nội dung bài học và từ đó hoàn thành tốt bài tập của mình. Đồng thời luôn đạt điểm cao trong các bài thi bài kiểm tra sắp tới. Chúc các em học tập thật tốt.

Đăng bởi THCS Bình Chánh trong chuyên mục Học tập