Giải Toán 10 Chân trời sáng tạo: Bài tập cuối chương 6 | Giải Toán lớp 10

Mời các em theo dõi nội dung bài học do thầy cô trường Trung học Bình Chánh biên soạn sẽ giúp các em nắm chắc kiến thức nội dung bài học tốt hơn.

Giải bài tập Toán 10 Bài tập cuối chương 6

Bài tập

Bạn đang xem: Giải Toán 10 Chân trời sáng tạo: Bài tập cuối chương 6 | Giải Toán lớp 10

Giải Toán 10 trang 126 Tập 1

Bài 1 trang 126 Toán lớp 10 Tập 1: Một hằng số quan trọng trong toán học là số e có giá trị gần đúng với 12 chữ số thập phân là 2,718281828459.

a) Giả sử ta lấy giá trị 2,7 làm giá trị gần đúng của e. Hãy chứng tỏ sai số tuyệt đối không vượt quá 0,02 và sai số tương đối không vượt quá 0,75%.

b) Hãy quy tròn e đến hàng phần nghìn.

c) Tìm số gần đúng của số e với độ chính xác 0,00002.

Lời giải:

a) Sai số tuyệt đối ∆ = |2,718281828459 – 2,7| = 0,018281828459 < 0,02.

Sai số tương đối $\delta =\frac{\Delta }{\left|2,7\right|}=\frac{0,018281828459}{2,7}\approx 0,68\%$ < 0,75%.

b) Quy tròn e đến hàng phần nghìn ta được số gần đúng là 2,718.

c) Hàng của chữ số khác 0 đầu tiên bên trái của độ chính xác d = 0,00002 là hàng phần trăm nghìn. Quy tròn e đến hàng phần trăm nghìn ta được số gần đúng của e là 2,71828.

Bài 2 trang 126 Toán lớp 10 Tập 1: Cho các số gần đúng a = 54919020 ± 1000 và b = 5,7914003 ± 0,002. Hãy xác định số quy tròn của a và b.

Lời giải:

a = 54 919 020 ± 1 000

Hàng lớn nhất của độ chính xác d = 1 000 là hàng nghìn, nên ta quy tròn đến hàng phần chục nghìn. Vậy số quy tròn của a là 54 920 000.

b = 5,7914003 ± 0,002

Hàng lớn nhất của độ chính xác d = 0,002 là hàng phần nghìn, nên ta quy tròn đến hàng phần trăm. Vậy số quy tròn của b là 5,79.

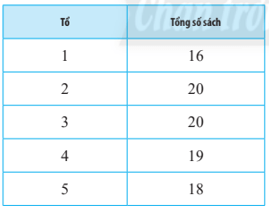
Bài 3 trang 126 Toán lớp 10 Tập 1: Mỗi học sinh lớp 10A đóng góp 2 quyển sách cho thư viện trường. Lớp trưởng thống kê lại số sách mà mỗi tổ trong lớp đóng góp ở bảng sau:

Hãy cho biết lớp trưởng đã thống kê chính xác chưa. Tại sao?

Lời giải:

Mỗi học sinh đóng góp 2 quyển sách nên tổng số sách của một tổ sẽ chia hết cho 2.

Ta thấy số sách quyên góp được của tổ 4 là 19, là số lẻ không chia hết cho 2 nên lớp trưởng thống kê chưa chính xác.

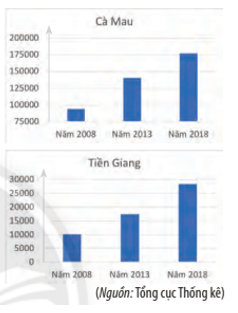
Bài 4 trang 126 Toán lớp 10 Tập 1: Sản lượng nuôi tôm phân theo địa phương của các tỉnh Cà Mau và Tiền Giang được thể hiện ở hai biểu đồ sau (đơn vị: tấn):

a) Hãy cho biết các phát biểu sau là đúng hay sai:

i. Sản lượng nuôi tôm mỗi năm của tỉnh Tiền Giang đều cao hơn tỉnh Cà Mau.

ii. Ở tỉnh Cà Mau, sản lượng nuôi tôm năm 2018 tăng gấp hơn 4 lần so với năm 2008.

iii. Ở tỉnh Tiền Giang, sản lượng nuôi tôm năm 2018 tăng gấp hơn 2,5 lần so với năm 2008.

iv. Ở tỉnh Tiền Giang, từ năm 2008 đến năm 2018, sản lượng nuôi tôm mỗi năm tăng trên 50% so với năm cũ.

v. Trong vòng 5 năm từ năm 2013 đến 2018, sản lượng nuôi tôm của tỉnh Cà Mau tăng cao hơn của tỉnh Tiền Giang.

b) Để so sánh sản lượng nuôi tôm của hai tỉnh Cà Mau và Tiền Giang, ta nên sử dụng loại biểu đồ nào?

Lời giải:

a)

+) Phát biểu i: Ta thấy cột sản lượng các năm 2008, 2013, 2018 của tỉnh Tiền Giang cao hơn tỉnh Cà Mau nên phát biểu i đúng.

+) Phát biểu ii: Ở tỉnh Cà Mau, sản lượng nuôi tôm năm 2018 là 175 000 tấn, sản lượng nuôi tôm năm 2008 khoảng 90 000 tấn.

Khi đó sản lượng nuôi tôm năm 2018 so với năm 2008 bằng $\frac{175000}{90000}=\frac{35}{18}$ ≈ 1,94 lần.

Do đó phát biểu ii sai.

+) Phát biểu iii: Ở tỉnh Tiền Giang, sản lượng nuôi tôm năm 2018 khoảng 29 000 tấn, sản lượng nuôi tôm năm 2008 là 10 000 tấn.

Khi đó sản lượng nuôi tôm năm 2018 so với năm 2008 bằng $\frac{29000}{10000}=\frac{29}{10}$ = 2,9 lần.

Do đó phát biểu iii đúng.

+) Phát biểu iv: Nếu sản lượng nuôi tôm mỗi năm ở tỉnh Tiền Giang tăng trên 50% so với năm cũ thì sản lượng năm 2009 ít nhất bằng 150% . 100 000 = 150 000 tấn.

Sản lượng năm 2010 ít nhất bằng 150% . 150 000 = 225 000 tấn, trong khi sản lượng năm 2013 chỉ đạt khoảng 180 000 tấn.

Do đó phát biểu iv sai.

+) Phát biểu v: Trong vòng 5 năm từ năm 2013 đến 2018, sản lượng nuôi tôm của tỉnh Cà Mau tăng 175 000 – 90 000 = 85 000 tấn, sản lượng nuôi tôm của tỉnh Tiền Giang tăng 290 000 – 180 000 = 110 000 tấn.

85 000 < 110 000 nên phát biểu v sai.

b) Để so sánh sản lượng nuôi tôm của hai tỉnh Cà Mau và Tiền Giang, ta nên sử dụng loại biểu đồ đường.

Giải Toán 10 trang 127 Tập 1

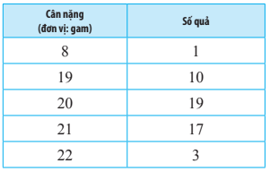
Bài 5 trang 127 Toán lớp 10 Tập 1: Bạn Châu cân lần lượt 50 quả vải thiều Thanh Hà được lựa chọn ngẫu nhiên từ vườn nhà mình và được kết quả như sau:

a) Hãy tìm số trung bình, trung vị, mốt của mẫu số liệu trên.

b) Hãy tìm độ lệch chuẩn, khoảng biến thiên, khoảng tứ phân vị và giá trị ngoại lệ của mẫu số liệu trên.

Lời giải:

a) Số trung bình của mẫu số liệu trên là:

$\frac{8.1+19.10+20.19+21.17+22.3}{1+10+19+17+3}$ = 20,02.

Cỡ mẫu bằng 50 nên tứ phân vị thứ hai bằng trung bình cộng của số liệu thứ 25 và 26 trong mẫu số liệu là Q₂ = $\frac{1}{2}$(20 + 20) = 20.

Mẫu số liệu trên có giá trị 20 xuất hiện nhiều nhất nên mốt của mẫu số liệu trên là 20.

b) Phương sai của mẫu số liệu trên là:

S² = $\frac{1}{50}$(1 . 8² + 10 . 19² + 19 . 20² + 17 . 21² + 3 . 22²) – 20,02² = 3,66.

Độ lệch chuẩn của mẫu số liệu trên là:

S = $\sqrt{3,66}$ ≈ 1,91.

Khoảng biến thiên của mẫu số liệu trên là: R = 22 – 8 = 14.

Tứ phân vị thứ nhất là trung vị của mẫu 8; 19; 20 với cỡ mẫu bằng 25 là số liệu thứ 13 của mẫu số liệu là Q₁ = 20.

 Tứ phân vị thứ nhất là trung vị của mẫu 20; 21; 22 với cỡ mẫu bằng 25 là số liệu thứ 38 của mẫu số liệu là Q₃ = 21.

Khoảng tứ phân vị của của mẫu số liệu trên là: 21 – 20 = 1.

Ta có Q₃ + 1,5${\Delta }_Q$ = 21 + 1,5 . 1 = 22,5 và Q₁– 1,5${\Delta }_Q$ = 20 – 1,5 . 1 = 18,5.

Do đó giá trị ngoại lệ của mẫu số liệu trên là 8.

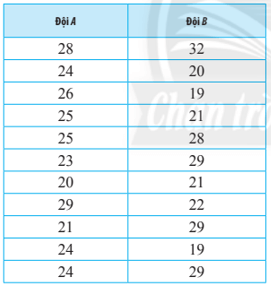
Bài 6 trang 127 Toán lớp 10 Tập 1: Độ tuổi của 22 cầu thủ ở đội hình xuất phát của hai đội bóng đá được ghi lại ở bảng sau:

a) Hãy tìm số trung bình, mốt, độ lệch chuẩn và tứ phân vị của tuổi mỗi cầu thủ của từng đội bóng.

b) Tuổi của các cầu thủ ở đội bóng nào đồng đều hơn? Tại sao?

Lời giải:

a) +) Đội A:

Sắp xếp tuổi của các cầu thủ theo thứ tự không giảm ta được mẫu:

20; 21; 23; 24; 24; 24; 25; 25; 26; 28; 29.

Số trung bình của mẫu số liệu trên là:

$\frac{1}{11}$(20 + 21 + 23 + 24 + 24 + 24 + 25 + 25 + 26 + 28 + 29) ≈ 24,45.

Trong mẫu số liệu trên, giá trị 24 xuất hiện nhiều nhất nên mốt của mẫu số liệu trên là 24.
Phương sai của mẫu số liệu trên là:

$\frac{1}{11}$(20² + 21² + 23² + 3 . 24² + 2 . 25² + 26² + 28² + 29²) – 24,45² ≈ 6,65.

Độ lệch chuẩn của mẫu số liệu trên là:

$\sqrt{6,65}$ ≈ 2,58.

Cỡ mẫu bằng 11 nên tứ phân vị thứ hai là số liệu thứ 6 trong mẫu số liệu là Q₂ = 24.

Tứ phân vị thứ nhất là trung vị của mẫu 20; 21; 23; 24; 24 nên Q₁ = 23.

Tứ phân vị thứ ba là trung vị của mẫu 25; 25; 26; 28; 29 nên Q₃ = 26.

+) Đội B:

Sắp xếp tuổi của các cầu thủ theo thứ tự không giảm ta được mẫu:

19; 19; 20; 21; 21; 22; 28; 29; 29; 29; 32.

Số trung bình của mẫu số liệu trên là:

$\frac{1}{11}$(19 + 19 + 20 + 21 + 21 + 22 + 28 + 29 + 29 + 29 + 32) ≈ 24,45.

Trong mẫu số liệu trên, giá trị 29 xuất hiện nhiều nhất nên mốt của mẫu số liệu trên là 29.
Phương sai của mẫu số liệu trên là:

$\frac{1}{11}$(2 . 19² + 20² + 2 . 21² + 22² + 28² + 3 . 29² + 32²) – 24,45² ≈ 22,11.

Độ lệch chuẩn của mẫu số liệu trên là:

$\sqrt{22,11}$ ≈ 4,7.

Cỡ mẫu bằng 11 nên tứ phân vị thứ hai là số liệu thứ 6 trong mẫu số liệu là Q₂ = 22.

Tứ phân vị thứ nhất là trung vị của mẫu 19; 19; 20; 21; 21 nên Q₁ = 20.

Tứ phân vị thứ ba là trung vị của mẫu 28; 29; 29; 29; 32 nên Q₃ = 29.

b) Độ lệch chuẩn giữa số tuổi của các cầu thủ ở đội A nhỏ hơn đội B nên tuổi của các cầu thủ ở đội A đồng đều hơn so với đội B.

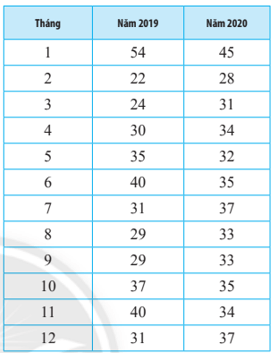
Bài 7 trang 127 Toán lớp 10 Tập 1: Một cửa hàng bán xe ô tô thay đổi chiến lược kinh doanh vào cuối năm 2019. Số xe cửa hàng bán được mỗi tháng trong năm 2019 và 2020 được ghi lại ở bảng sau:

a) Hãy tính số trung bình, khoảng tứ phân vị và độ lệch chuẩn của số lượng xe bán được trong năm 2019 và năm 2020.

b) Nêu nhận xét về tác động của chiến lược kinh doanh mới lên số lượng xe bán ra hằng tháng.

Lời giải:

a) +) Năm 2019:

Sắp xếp số lượng xe bán được theo thứ tự không giảm ta được mẫu:

22; 24; 29; 29; 30; 31; 31; 35; 37; 40; 40; 54.

Số trung bình của mẫu số liệu trên là:

$\frac{1}{12}$(22 + 24 + 29 + 29 + 30 + 31 +  31 +  35 + 37 +  40 + 40 + 54) = 33,5.

Phương sai của mẫu số liệu trên là:

$\frac{1}{12}$(22² + 24² + 2. 29² + 30² + 2 . 31² + 35² + 37² + 2 . 40² + 54²) – 33,5² = 67,25.

Độ lệch chuẩn của mẫu số liệu trên là:

$\sqrt{67,25}$ ≈ 8,2.

Cỡ mẫu bằng 12 nên tứ phân vị thứ hai của mẫu số liệu bằng trung bình cộng của số liệu thứ 6 và thứ 7 là Q₂ = $\frac{1}{2}$(31 + 31) = 31.

Tứ phân vị thứ nhất là trung vị của mẫu 22; 24; 29; 29; 30; 31 nên tứ phân vị thứ nhất là Q₁ = $\frac{1}{2}$(29 + 29) = 29.

Tứ phân vị thứ ba là trung vị của mẫu 31; 35; 37; 40; 40; 54 nên tứ phân vị thứ ba là Q₃ = $\frac{1}{2}$(37 + 40) = 38,5.

Khoảng tứ phân vị của mẫu số liệu trên là: 38,5 – 29 = 9,5.

+) Năm 2020:

Sắp xếp số lượng xe bán được theo thứ tự không giảm ta được mẫu:

28; 31; 32; 33; 33; 34; 34; 35; 35; 37; 37; 45.

Số trung bình của mẫu số liệu trên là:

$\frac{1}{12}$(28 + 31 + 32 + 33 + 33 + 34 + 34 + 35 + 35 + 37 + 37 + 45) ≈ 34,58.

Phương sai của mẫu số liệu trên là:

$\frac{1}{12}$(28² + 31² + 32² + 2 . 33² + 2 . 34² + 2 . 35² + 2 . 37² + 45²) – 34,58² ≈ 10,22.

Độ lệch chuẩn của mẫu số liệu trên là:

$\sqrt{10,22}$ ≈ 3,2.

Cỡ mẫu bằng 12 nên tứ phân vị thứ hai của mẫu số liệu bằng trung bình cộng của số liệu thứ 6 và thứ 7 là Q₂ = $\frac{1}{2}$(34 + 34) = 34.

Tứ phân vị thứ nhất là trung vị của mẫu 28; 31; 32; 33; 33; 34 nên tứ phân vị thứ nhất là Q₁ = $\frac{1}{2}$(32 + 33) = 32,5.

Tứ phân vị thứ ba là trung vị của mẫu 34; 35; 35; 37; 37; 45 nên tứ phân vị thứ ba là Q₃ = $\frac{1}{2}$(35 + 37) = 36.

Khoảng tứ phân vị của mẫu số liệu trên là: 36 – 32,5 = 3.5

b) Sau khi áp dụng chiến lược kinh doanh mới, số lượng xe bán ra hàng tháng đồng đều hơn.

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Dùng máy tính cầm tay để tính toán với số gần đúng và tính các số đặc trưng của mẫu số liệu thống kê

Bài 2: Dùng bảng tính để tính các số đặc trưng của mẫu số liệu thống kê

Bài 1: Mệnh đề

Bài 2: Tập hợp

Bài 3: Các phép toán trên tập hợp

Xem thêm tài liệu Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài tập cuối chương 6

Đăng bởi: THCS Bình Chánh

Chuyên mục: Toán 10 Chân trời sáng tạo

• Giải Bài 4.16 trang 65 Toán 10 tập 1 SGK Kết nối tri thức với cuộc sống
• Giải Bài 1 trang 37 Toán 10 tập 1 SGK Chân trời sáng tạo
• Giải Vận dụng trang 30 Toán 10 tập 1 SGK Kết nối tri thức với cuộc sống
• Triều cường là gì? Triều cường xảy ra khi nào?
• Thơ Đường luật là gì? Đặc điểm của thơ Đường luật
• Phân tích nhân vật he ra clet hay nhất (5 mẫu)