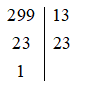Toán 6 Bài 11 Cánh diều: Phân tích một số ra thừa số nguyên tố | Giải SGK Toán lớp 6 Cánh diều

Mời các em theo dõi nội dung bài học do thầy cô trường Trung học Bình Chánh biên soạn sẽ giúp các em nắm chắc kiến thức nội dung bài học tốt hơn.

Giải Toán 6 Bài 11: Phân tích một số ra thừa số nguyên tố

Trả lời câu hỏi giữa bài

Bạn đang xem: Toán 6 Bài 11 Cánh diều: Phân tích một số ra thừa số nguyên tố | Giải SGK Toán lớp 6 Cánh diều

Giải Toán 6 trang 44 Tập 1

Toán lớp 6 trang 44 Câu hỏi khởi động: Làm thế nào để viết số 120 thành tích của các thừa số nguyên tố?

Lời giải:

Sau bài học này, ta sẽ biết 2 phương pháp để viết số 120 thành tích các thừa số nguyên tố.

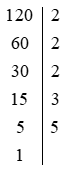
PP 1. Viết theo cột dọc:

Do đó: 120 = 2 . 2 . 2 . 3 . 5 = 2³ . 3 . 5.

PP 2. Viết rẽ nhánh:

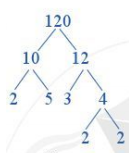
Cách 1: 120 = 10 . 12

Vậy 120 = 2 . 5 . 3 . 2 . 2 = 2³ . 3. 5

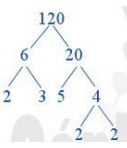
Cách 2: 120 = 6 . 20

Vậy 120 = 2 . 3 . 5 . 2 . 2 = 2³ . 3 . 5.

Toán lớp 6 trang 44 Hoạt động 1:

a) Hãy nêu các số nguyên tố nhỏ hơn 30.

b) Tìm một ước nguyên tố của 91.

Lời giải:

a) Theo phần “Có thể em chưa biết” (Trang 43/SGK), các số nguyên tố nhỏ hơn 30 là:

2; 3; 5; 7; 11; 13; 17; 19; 23; 29.

b) Trước tiên ta tìm các ước của số 91 bằng cách lấy 91 lần lượt chia cho các số tự nhiên từ 1 đến 91, ta được các ước của 91 là: 1; 7; 13; 91, trong đó có 7 và 13 là các số nguyên tố.

Vậy các ước nguyên tố của 91 là: 7 và 13.

Do đó ta trả lời: “Một ước nguyên tố của 91 là 7” hoặc “Một ước nguyên tố của 91 là 13”.

Toán lớp 6 trang 44 Luyện tập 1: Tìm một ước nguyên tố của 187.

Lời giải:

Áp dụng kiến thức:

Để tìm một ước nguyên tố của số a ta có thể làm như sau: lần lượt thực hiện phép chia a cho các số nguyên tố theo thứ tự tăng dần 2, 3, 5, 7, 11, 13, …

Khi đó, phép chia hết đầu tiên cho ta số chia là một ước nguyên tố của a.

Vậy ta tìm một ước nguyên tố của 187 như sau:

Ta lần lượt thực hiện phép chia 187 cho các số nguyên tố theo thứ tự tăng dần 2, 3, 5, 7, 11, 13…

+ Theo dấu hiệu chia hết, số 187 không chia hết cho các số 2, 3, 5.

+ 187 : 7 = 26 (dư 5), nên 187 không chia hết cho 7.

+ Ta có: 187 = 11 . 17

 Vậy 11 là một ước nguyên tố của 187.

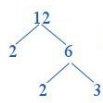
Toán lớp 6 trang 44 Hoạt động 2: Viết số 12 thành tích của các thừa số nguyên tố.

Lời giải:

Cách 1. Quan sát và thực hiện lần lượt:

+) Tìm một ước nguyên tố của 12, chẳng hạn là 2.

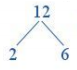
+) Viết số 12 thành tích của 2 với một thừa số khác: 12 = 2 . 6

Vẽ hai nhánh từ số 12 cho hai thừa số 2 và 6.

+) Tiếp tục tìm một ước nguyên tố của 6, chẳng hạn là 2.

+) Viết số 6 thành tích của 2 với một thừa số khác: 6 = 2 . 3

Vẽ tiếp hai nhánh từ số 6 cho hai thừa số 2 và 3.

+) Các thừa số 2 và 3 đều là số nguyên tố nên ta dừng lại.

Lấy tích tất cả các thừa số ở cuối cùng mỗi nhánh, ta có:  

Các thừa số trong tích cuối cùng đều là số nguyên tố. Ta nói số 12 đã được phân tích ra thừa số nguyên tố.

Cách 2. Ta có thể viết lại quá trình phân tích số 12 ra thừa số nguyên tố “theo cột dọc” như sau:

Lấy 12 chia cho ước nguyên tố 2.

Lấy thương là 6 chia tiếp cho ước nguyên tố 2.

Lấy thương 3 chia tiếp cho ước nguyên tố 3

Vậy ta phân tích được: $12=\mathrm{2.2.3}=2^2.3$.

Giải Toán 6 trang 45 Tập 1

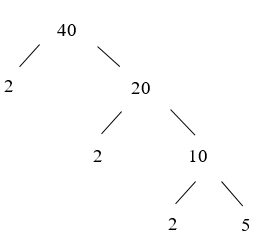
Toán lớp 6 trang 45 Luyện tập 2: Phân tích số 40 ra thừa số nguyên tố bằng cách viết “rẽ nhánh” và “theo cột dọc”

Lời giải:

+ Cách viết “rẽ nhánh”:

+ Cách viết “theo cột dọc”:

Vậy ta phân tích được: 40 = 2 . 2 . 2 . 5 = 2³ . 5.

Giải Toán 6 trang 46 Tập 1

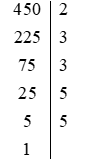
Toán lớp 6 trang 46 Luyện tập 3: Phân tích số 450 ra thừa số nguyên tố.

Lời giải:

Cách 1: Ta có: 450 = 10 . 45

Vậy 450 = 2 . 5 . 3 . 3 . 5 = 2 . 3² . 5².

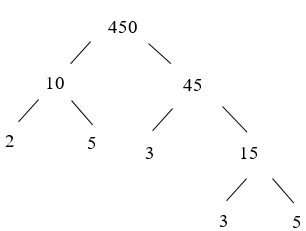
Cách 2: Ta có: 450 = 9 . 50

Vậy 450 = 3 . 3 . 2 . 5 . 5 = 2 . 3² . 5².

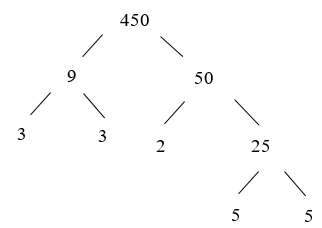
Cách 3. Ta phân tích “theo cột dọc”.

Vậy ta 450 = 2 . 3 . 3 . 5 . 5 = 2 . 3² . 5².

Bài tập

Toán lớp 6 trang 46 Bài 1: Phân tích các số sau ra thừa số nguyên tố: 45, 78, 270, 299.

Lời giải:

Học sinh có thể phân tích bằng cách viết “rẽ nhánh” hoặc “theo cột dọc”.

Có thể trình bày như sau:

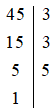
+) Phân tích số 45 bằng cách viết “theo cột dọc”

Vậy 45 = 3 . 3. 5 = 3² . 5.

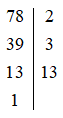
+) Phân tích số 78 bằng cách viết “theo cột dọc”:

Vậy 78 = 2 . 3. 13.

+) Phân tích số 270 bằng cách viết “rẽ nhánh”:

Ta có: 270 = 10 . 27

Vậy 270 = 2 . 5 . 3 . 3. 3 = 2 . 3³ . 5.

+) Phân tích số 299 bằng cách viết “theo cột dọc”:

Vậy 299 = 13 . 23.

Toán lớp 6 trang 46 Bài 2:

a) Biết 400 = 2⁴ . 5². Hãy viết 800 thành tích các thừa số nguyên tố.

b) Biết 320 = 2⁶ . 5. Hãy viết 3 200 thành tích các thừa số nguyên tố.

Lời giải:

a) Ta có: 800 = 2 . 400

Mà 400 = 2⁴ . 5²

Do đó: 800 = 2 . (2⁴ . 5²) = (2¹ . 2⁴). 5² = 2⁴⁺¹ . 5² = 2⁵ . 5²

Vậy 800 = 2⁵ . 5².

b) Ta có: 3 200 = 10 . 320

Mà 10 = 2 . 5 và 320 = 2⁶ . 5

Do đó: 3 200 = (2 . 5) . (2⁶ . 5)

= (2¹ . 2⁶) . (5 . 5)

= 2¹⁺⁶ . 5² = 2⁷ . 5²

Vậy 3 200 = 2⁷ . 5².

Toán lớp 6 trang 46 Bài 3:

a) Biết 2 700 = 2² . 3³ . 5². Hãy viết 270 và 900 thành tích các thừa số nguyên tố.

b) Biết 3 600 = 2⁴ . 3² . 5². Hãy viết 180 và 600 thành tích các thừa số nguyên tố.

Lời giải:

a) Ta có: 2 700 =  10 . 270 = 3 . 900

Mà 10 = 2 . 5 và 2 700 = 2² . 3³ . 5²

Do đó: 270 = 2 700 : 10

= (2² . 3³ . 5²) : (2 . 5)

= (2² : 2) . 3³ . (5² : 5)

= 2 . 3³ . 5

900 = 2 700 : 3

= (2² . 3³ . 5²) : 3

= 2² . (3³ : 3) . 5²

= 2² . 3² .5²

Vậy 270 = 2 . 3³ . 5

và 900 = 2² . 3² .5².

b) Ta có: 3 600 = 20 . 180 = 6 . 600

Mà 20 = 2 . 10 = 2 . 2 . 5

= 2² . 5; 6 = 2 . 3

và 3 600 = 2⁴ . 3² . 5²

Do đó: 180 = 3 600 : 20

= (2⁴ . 3² . 5²) : (2² . 5)

= (2⁴ : 2²) . 3² .(5² : 5)

= 2^4-2 . 3² . 5 = 2² . 3² . 5

600 = 3 600 : 6

= (2⁴ . 3² . 5²) : (2 . 3)

= (2⁴ : 2) . (3²: 3) . 5²

= 2^4-1 . 3 . 5² = 2³ . 3 . 5²

Vậy 180 = 2² . 3² . 5

và 600 = 2³ . 3 . 5².

Toán lớp 6 trang 46 Bài 4: Chỉ ra hai số tự nhiên mà mỗi số đó có đúng ba ước nguyên tố.

Lời giải:

Ta lấy tích của ba số nguyên tố khác nhau bất kì, ta được số tự nhiên có đúng ba ước nguyên tố.

Ví dụ: 2 . 3. 5 = 30;

3 . 5 . 7 = 105;

5. 7 . 11 = 385; …

Vậy hai số tự nhiên mà mỗi số có đúng 3 ước nguyên tố là: 30; 105.

(Tương tự cách làm trên, các em có thể chọn hai số khác thỏa mãn yêu cầu).

Toán lớp 6 trang 46 Bài 5: Phân tích số 84 ra thừa số nguyên tố rồi tìm tập hợp các ước của nó.

Lời giải:

+) Phân tích 84 ra thừa số nguyên tố bằng cách viết “theo cột dọc”:

Do đó: 84 = 2 . 2 . 3 . 7 = 2² . 3 . 7

+ Khi đó ta có phân tích

84 = 1 . 84 = 2. 42 = 3 . 28 = 4 . 21 = 6 . 14 = 7 . 12

Do đó các ước của 84 là: 1; 2; 3; 4; 6; 7; 12; 14; 21; 28; 42; 84.

Giả sử A là tập hợp các ước của 84.

Vậy A = {1; 2; 3; 4; 6; 7; 12; 14; 21; 28; 42; 84}.

Xem thêm lời giải bài tập Toán lớp 6 sách Cánh diều hay, chi tiết khác:

Bài 10: Số nguyên tố. Hợp số

Bài 11: Phân tích một số ra thừa số nguyên tố

Bài 12: Ước chung và ước chung lớn nhất

Bài 13: Bội chung và bội chung nhỏ nhất

Bài tập cuối chương 1

Đăng bởi: THCS Bình Chánh

Chuyên mục: Toán 6 Cánh Diều

• Tưởng tượng em ở trong phòng khách của một tàu ngầm và tàu đang lặn xuống đáy biển, dưới mặt nước năm mươi mét. Hãy ghi lại những hình dung của em về cảnh vật trong không gian đó (5 mẫu)
• Có ý kiến cho rằng việc nuôi chó mèo trong nhà không những không có tác dụng gì mà còn rất mất vệ sinh. Em có tán thành suy nghĩ này không? Hãy nêu ý kiến của em và nêu ra những lí lẽ, bằng chứng để làm sáng tỏ ý kiến ấy (10 mẫu)
• Giới thiệu một nhân vật có tấm lòng nhân hậu trong các văn bản truyện đã học ở sách Ngữ văn 6, tập 2 và nêu lí do em thích nhân vật này (8 mẫu)
• Vì sao cuối học kì 1, lớp em được tuyên dương và khen thưởng là lớp đứng đầu khối 6?
• Viết một đoạn văn ngắn khoảng 4-5 dòng nói về cảm xúc của em khi xem một buổi biểu diễn văn nghệ hoặc một cuộc thi thể thao (24 mẫu)
• Viết đoạn văn (khoảng 4-6 dòng) tóm tắt nội dung truyện Nắng trưa bồi hồi lớp 6 (20 mẫu)