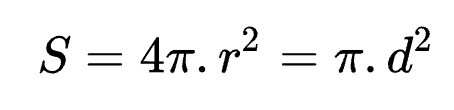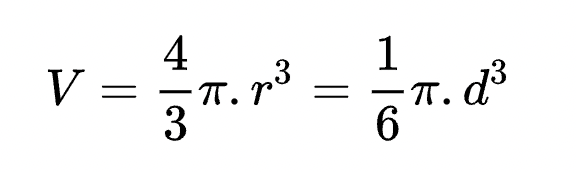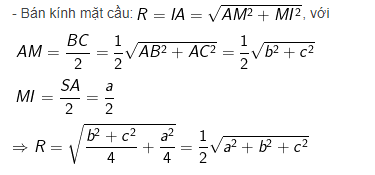Công thức hình cầu lớp 9 và bài tập vận dụng

Cô Nguyễn Thanh Phương 02/06/2023

Mời các em theo dõi nội dung bài học về Công thức hình cầu lớp 9 và bài tập vận dụng do thầy cô trường THCS Bình Chánh biên soạn. Hy vọng sẽ là tài liệu hữu ích giúp các em học tốt và hoàn thành tốt bài tập của mình.

Mục lục

Hình cầu là gì? Mặt cầu là gì?

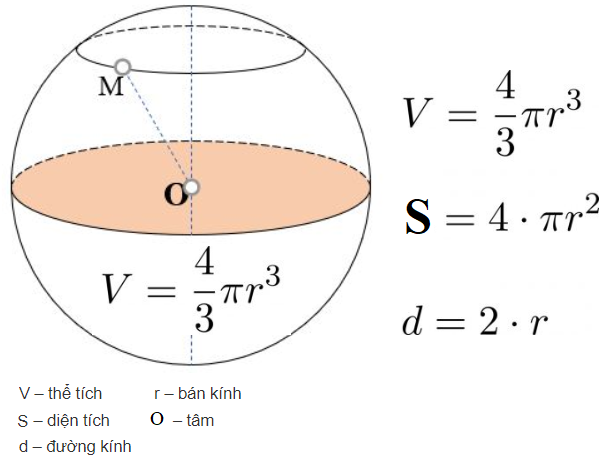
Theo định nghĩa toán học, trong không gian ba chiều, khi quay nửa hình tròn (O, R) 1 vòng quanh đường kính AB cố định thì được 1 hình cầu.

Nửa đường tròn trong phép quay trên là 1 mặt cầu.
Điểm O là tâm hình cầu và R là bán kính của hình cầu hay mặt cầu đó.

Bạn đang xem: Công thức hình cầu lớp 9 và bài tập vận dụng

Mặt cầu là tập hợp các điểm nằm cách đều điểm O (tâm hình cầu) 1 khoảng cố định cho trước không đổi = R (bán kính) tức R= OA.

* Tính chất của hình cầu

Trục đối xứng của hình cầu là bất kỳ đường thẳng nào giao nhau với hình cầu và đi qua tâm của nó. Khi đó, xoay 1 quả cầu xung quanh trục này ở bất kỳ góc độ nào cũng sẽ biến nó thành chính nó.
Mặt phẳng phản xạ là một mặt phẳng cắt hình được đề cập qua tâm của nó chia hình cầu thành hai phần bằng nhau.

Công thức hình cầu lớp 9

Công thức tính diện tích mặt cầu

Theo định nghĩa, diện tích mặt cầu được tính bằng 4 lần diện tích hình tròn lớn, hay bằng bốn lần hằng số Pi nhân với bình phương bán kính của hình cầu.

Trong đó:

S là diện tích mặt cầu
r là bán kính mặt cầu/hình cầu
d là đường kính mặt cầu/hình cầu
π là 3.14

Công thức tính thể tích hình cầu (khối cầu)

Theo định nghĩa, thể tích hình cầu (hay thể tích khối cầu) được tính bằng ba phần tư của Pi nhân với lập phương bán kính hình cầu.

Như vậy, để tính thể tích khối cầu, chỉ cần tìm bán kính hình cầu (hoặc đường kính). Sau đó thay áp dụng vào công thức V = ⁴⁄₃πr³ để tính.

V là thể tích khối cầu (đơn vị m3)
π là số pi, có giá trị sấp sỉ 3,14
r là bán kính khối cầu
d là bán kính mặt cầu/hình cầu

Lưu ý: Đơn vị của thể tích là đơn vị khối (cm3, m3,…)

Hướng dẫn cách tính thể tích hình cầu

Bước 1: Viết công thức tính hình cầu ra giấy

Đầu tiên, bạn viết ra giấy công thức tính thể tích hình cầu: V = ⁴⁄₃π.r³.

Bước 2: Đọc đề tìm bán kính

Sau đó, bạn đọc đề nếu đề cho sẳn bán kính thì bạn ghi ra giấy. Nhưng nếu đề cho bạn đường kính thì bạn có thể áp dụng công thức V = 1⁄6π.d³.

Hoặc bạn cũng có thể lấy đường kính chia 2 để ra bán kính rồi áp dụng công thức như bước 1.

Giả sử trong trường hợp khó hơn, đề chỉ cho bạn diện dích mặt cầu (S). Bạn có thể tìm bán kính bằng cách lấy diện tích mặt cầu chia cho 4π, sau đó tính căn bậc hai của kết quả này là ra. Có nghĩa là:

r = √(S/4π) (“bán kính bằng căn bậc hai của thương số diện tích và 4π”).

Bước 3: Tiến hành tính luỹ thừa bậc 3 của bán kính

Tới đây, bạn chỉ cần tính luỹ thừa bậc 3 của bán kính bằng cách đem bán kính nhân ba lần với chính nó hoặc nâng nó lên số mũ ba

Ví dụ: (1 cm)³ = 1 cm x 1 cm x 1 cm = 1

(2 cm)³ = 2 cm x 2 cm x 2 cm = 8

Bước 4: Tiếp tục nhân luỹ thừa bậc 3 của bán kính với 4/3

Tiếp đến, bạn bạn thay giá trị r³ vừa tính được vào công thức V = ⁴⁄₃πr³ để phương trình gọn hơn. Ví dụ đường tròn có bán kính là 1cm:

4/3 x 1 = 4/3
V = ⁴⁄₃ x π x 1, hay V = ⁴⁄₃π.

Bước 5: Nhân biểu thức vừa tính được với π (số pi)

Cuối cùng, bạn đặt π vào phép tính và nhân giá trị của nó với 4/3. Trong đó, giá trị của π tương đương với 3.14159. Nếu không bạn cũng có thể để nguyên π trong đáp án theo dạng V = ⁴⁄₃π là xong.

Ví dụ: V = 3.14159 x 4/3 = 4.1887.

Kết luận thể tích của hình cầu với bán kính bằng 1 là 4.19 cm³

Các bước giải bài tập công thức hình cầu lớp 9

Để tính thể tích khối cầu, chúng ta áp dụng ghi nhớ 3 bước như sau:

Bước 1: Phải thuộc công thức tính thể tích khối cầu, hãy ghi chúng ra giấy nháp, để tiện áp dụng công thức

Bước 2: Tìm bán kính hình cầu

Có 2 trường hợp

TH1: Đề bài toán đã cho bán kính thì chúng ta đến bước 3 (bước áp dụng công thức)
TH2: Đề cho đường kính, chia đôi để được bán kính. Ví dụ, đường kính d = 20cm ⇒ bán kính r = 10cm.

Bước 3: Thay bán kính vừa tìm được vào công thức tính thể tích khối cầu V = ⁴⁄₃πr³, sau đó nhận đáp án đúng.

Bài tập vận dụng công thức hình cầu lớp 9

Bài 1: Có đường tròn tâm O, bán kính là 9m. Hãy tính diện tích hình cầu?

Giải: Trước tiên, khi đã có bán kính của mặt cầu bạn tiến hành thay vào công thức Smặt cầu = 4 π.R^2, bạn được:

S = 4 x 3,14 x 9^2 = 1017.36 m2

Bài 2: Cho đường tròn tâm O, đường kính 2,5 cm. Hãy tính diện tích mặt cầu

Giải: Để tính diện tích hình cầu trong trường hợp này bạn cũng thay đường kính vào công thức Smặt cầu = π. d2, bạn được:

S = 3,14 x 2,5^2 = 19,625 cm2

Bài 3: Cho hình cầu có đường kính d = 6cm. Diện tích mặt cầu là:

A. 36π (cm2)

B. 9π (cm2)

C. 12π (cm2)

D. 36π (cm2)

Giải:

Vì đường kính d= 6cm >> Nên bán kính hình cầu R= d/2 = 3cm
Diện tích mặt cầu: S = 4πR^2 = 4π3^2 = 36 π (cm^2)

Bài 4: Tính thể tích khối cầu có đường kính d = 4 cm.

Giải:

Bán kính r = d/2 = 2 cm

Thể tích khối cầu là: V = ⁴⁄₃πr³ = 4/3.3,14.(2)³ = 33,49 cm³

Bài 5: Cho mặt cầu có thể tích V = 288π (cm³). Tính đường kính mặt cầu:

Ta có: V = ⁴⁄₃πr³ = 288π -> r = 6cm

Từ đó đường kính của mặt cầu là: d = 2r = 2.6 =12cm

Bài 6: Một mặt cầu có đường kính là d = 1,5 cm. Hãy tính thể tích mặt cầu?

Giải:

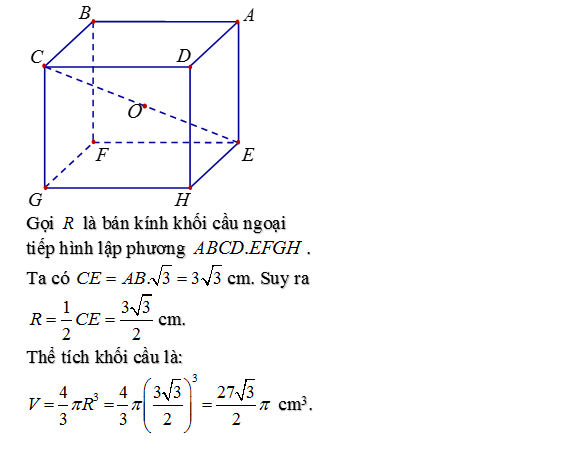
Bài 7: Thể tích khối cầu ngoại tiếp hình lập phương cạnh 3cm là?

Giải:

Câu 8: Hình chóp S.ABC có đáy là tam giác ABC vuông tại A, SA vuông góc với mặt phẳng (ABC) và SA = a, AB = b, AC = c. Mặt cầu đi qua các đỉnh A, B, C, S có bán kính r bằng bao nhiêu?

Giải:

***

Trên đây là nội dung bài học Công thức hình cầu lớp 9 và bài tập vận dụng do thầy cô trường THCS Bình Chánh biên soạn và tổng hợp. Hy vọng sẽ giúp các em hiểu rõ nội dung bài học và từ đó hoàn thành tốt bài tập của mình. Đồng thời luôn đạt điểm cao trong các bài thi bài kiểm tra sắp tới. Chúc các em học tập thật tốt.

Đăng bởi THCS Bình Chánh trong chuyên mục Học tập