Giải Luyện tập 2 trang 81 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống

Trường THCS Bình Chánh 25/07/2023

Mời các em theo dõi nội dung bài học do thầy cô trường THCS Bình Chánh biên soạn sẽ giúp các em nắm chắc kiến thức nội dung bài học tốt hơn.

Mục lục

Luyện tập 2 trang 81 SGK Toán 7 tập 2

Toán 7 tập 2 Luyện tập 2 trang 81 là lời giải bài Sự đồng quy của ba đường trung trực, ba đường cao SGK Toán 7 sách Kết nối tri thức với cuộc sống hướng dẫn chi tiết lời giải giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 7. Mời các em học sinh cùng tham khảo chi tiết.

Giải Luyện tập 2 Toán 7 trang 81

Luyện tập 2 (SGK trang 81): a) Chứng minh rằng trong tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó.

Bạn đang xem: Giải Luyện tập 2 trang 81 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống

b) Chứng minh rằng trong tam giác đều, điểm cách đều ba đỉnh cũng cách đều ba cạnh của tam giác.

Hướng dẫn giải

+ Ba đường trung trực của một tam giác đồng quy tại một điểm. Điểm này cách đều ba đỉnh của tam giác.

+ Ba đường cao của một tam giác đồng quy tại một điểm. Điểm đồng quy của ba đường cao gọi là trực tâm của tam giác đó.

Lời giải chi tiết

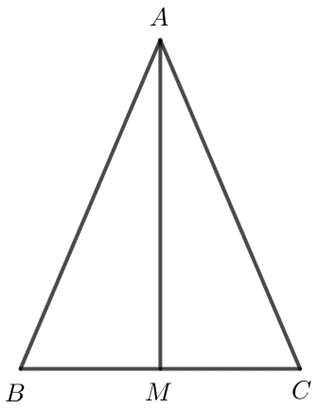
a) Hình vẽ minh họa:

Gọi M là trung điểm của BC

Do tam giác ABC cân tại A nên AB = AC và $\widehat {ABM} = \widehat {ACM}$

Do AB = AC nên A nằm trên đường trung trực của BC.

=> AM ⊥ BC nên AM là đường cao của tam giác ABC.

Xét tam giác ABM có:

$\widehat {ABM} + \widehat {MAB} = {90^0}$ (trong tam giác vuông, hai góc nhọn phụ nhau).

=> $\widehat {MAB} = {90^0} - \widehat {ABM}\left( * \right)$

Xét tam giác ACM có:

$\widehat {ACM} + \widehat {MAC} = {90^0}$ (trong tam giác vuông, hai góc nhọn phụ nhau).

=> $\widehat {MAC} = {90^0} - \widehat {ACM}\left( {**} \right)$

Mà $\widehat {ABM} = \widehat {ACM}$

Từ (*) và (**) ta có:

=> AM là tia phân giác của $\widehat {BAC}$

Vậy đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác ABC.

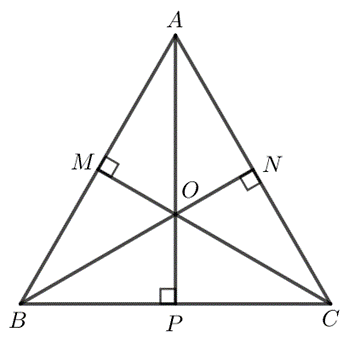
b) Hình vẽ minh họa:

Trong tam giác ABC đều có điểm O là điểm cách đều 3 đỉnh của tam giác.

Gọi M, N, P lần lượt là trung điểm của AB, AC, BC.

Do O cách đều 3 đỉnh của tam giác ABC nên O là giao điểm 3 đường trung trực của tam giác ABC.

=> OM ⊥ AM, ON ⊥ AN, OP ⊥ CP.

Tam giác ABC đều => AB = AC = BC.

Do M, N, P lần lượt là trung điểm của AB, AC, BC nên AM = AN = NC = CP.

Xét tam giác OAM vuông tại M và tam giác OAN vuông tại N:

AM = AN (chứng minh trên)

OA chung

=> ∆OAM = ∆OAN (cạnh huyền – cạnh góc vuông)

=> OM = ON (2 cạnh tương ứng) (1)

Xét tam giác OCN vuông tại N và tam giác OCP vuông tại P:

CN = CP (chứng minh trên)

OC chung

=> ∆OCN = ∆OCP (cạnh huyền – cạnh góc vuông)

=> ON = OP (2 cạnh tương ứng) (2)

Từ (1) và (2) suy ra OM = ON = OP

Vậy trong tam giác đều, điểm cách đều ba đỉnh cũng cách đều ba cạnh của tam giác.

Câu hỏi cùng bài:

Bài 9.26 trang 81 SGK Toán 7 tập 2
Bài 9.28 (SGK trang 81): Xét điểm O cách đều ba đỉnh của tam giác ABC …
Bài 9.29 (SGK trang 81): a) Có một chi tiết máy (đường viền ngoài là đường tròn) bị gãy…
Bài 9.30 (SGK trang 81): Cho hai đường thẳng không vuông góc b, c cắt nhau…

Bài tiếp theo: Giải Toán 7 Luyện tập chung trang 83 KNTT

—————————————-

Trên đây là lời giải chi tiết Luyện tập 2 Toán 7 trang 81 Sự đồng quy của ba đường trung trực, ba đường cao cho các em học sinh tham khảo, nắm được cách giải các dạng toán của Chương 9: Quan hệ giữa các yếu tố trong một tam giác. Qua đó giúp các em học sinh ôn tập chuẩn bị cho các bài thi giữa và cuối học kì lớp 7. Chúc các em học tốt.

Đăng bởi: THCS Bình Chánh

Chuyên mục: Toán 7 Kết nối tri thức