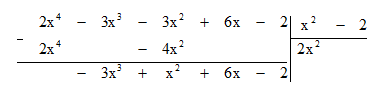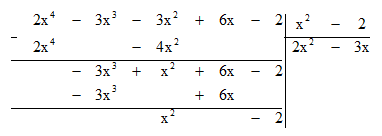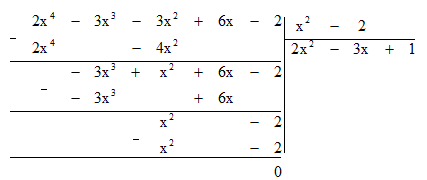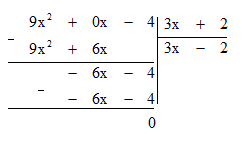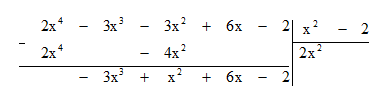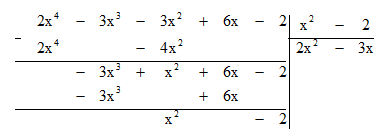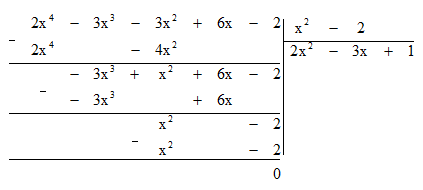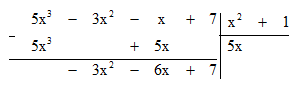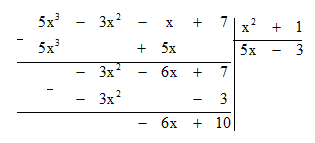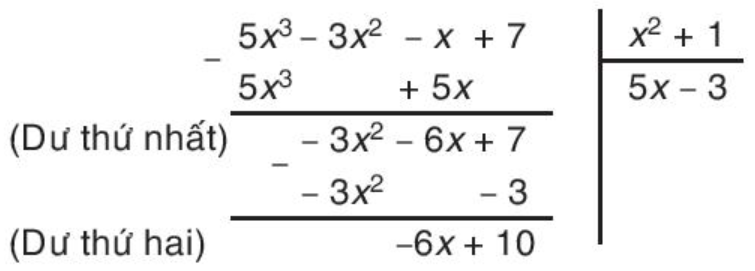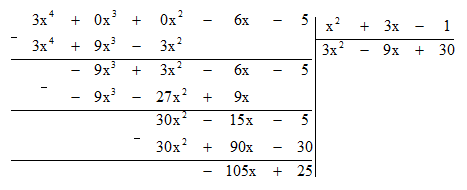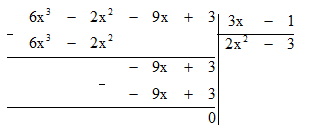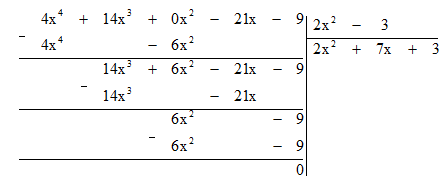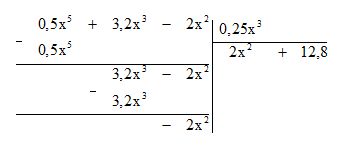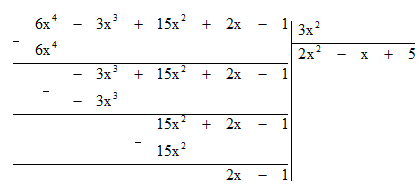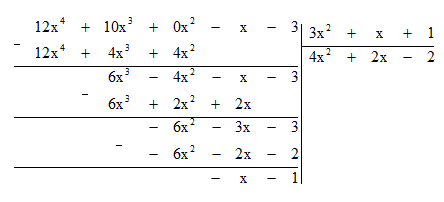Giải Toán 7 Bài 28 Kết nối tri thức: Phép chia đa thức một biến

Mời các em theo dõi nội dung bài học do thầy cô trường Trung học Bình Chánh biên soạn sẽ giúp các em nắm chắc kiến thức nội dung bài học tốt hơn.

Giải bài tập Toán 7 Bài 28: Phép chia đa thức một biến 

A. Các câu hỏi trong bài

Bạn đang xem: Giải Toán 7 Bài 28 Kết nối tri thức: Phép chia đa thức một biến

Giải Toán 7 trang 39 Tập 2

Mở đầu trang 39 Toán 7 Tập 2:

Bài toán: Tìm đa thức P sao cho A = B . P, trong đó

A = 2x⁴ – 3x³ – 3x² + 6x – 2 và B = x² – 2.

Tròn: “Mình nghĩ mãi là chưa giải được bài toán này. Vuông có cách nào giải không?”

Vuông: “Ừ nhỉ! Nếu A và B là hai số thì chỉ việc lấy A chia cho B là xong nhưng A và B lại là hai đa thức”.

Anh Pi: “Cũng thế thôi các em ạ. Trước hết các em phải tìm hiểu cách chia hai đa thức”.

Lời giải:

Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

Thực hiện theo các bước sau:

Bước 1: Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B:

2x⁴ : x² = 2x².

Bước 2: Lấy A trừ đi tích B . 2x² ta được dư thứ nhất là -3x³ + x² + 6x – 2.

Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B:

(-3x³) : x² = -3x.

Bước 4: Lấy dư thứ nhất trừ đi tích B . (-3x) ta được dư thứ hai là x² – 2.

Bước 5: Lấy hạng tử bậc cao nhất của dư thứ hai chia cho hạng tử bậc cao nhất của B:

x² : x² = 1.

Bước 6: Lấy dư thứ hai trừ đi tích B . 1 ta được dư thứ ba là 0.

Dư cuối cùng bằng 0 nên quá trình chia kết thúc.

Vậy A : B = 2x² – 3x + 1.

Giải Toán 7 trang 40 Tập 2

HĐ 1 trang 40 Toán 7 Tập 2:

Tìm thương của mỗi phép chia hết sau:

a) 12x³ : 4x; b) (-2x⁴) : x⁴; c) 2x⁵ : 5x².

Lời giải:

a) 12x³ : 4x =$\frac{12x^3}{4x}=3x^2$.

b) (-2x⁴) : x⁴ = $\frac{-2x^4}{x^4}=-2$.

c) 2x⁵ : 5x² =$\frac{2x^5}{5x^2}=\frac{2}{5}{x}^3$.

HĐ 2 trang 40 Toán 7 Tập 2:

Giả sử x ≠ 0. Hãy cho biết:

a) Với điều kiện nào (của hai số mũ) thì thương hai lũy thừa của x cũng là một lũy thừa của x với số mũ nguyên dương?

b) Thương hai lũy thừa của x cùng bậc bằng bao nhiêu?

Lời giải:

a) Gọi hai lũy thừa của x lần lượt là x^m và xⁿ (m, n ∈ ℕ).

Khi đó thương hai lũy thừa của x là: x^m : xⁿ = x^m-n.

Để x^m-n là lũy thừa của x với số mũ nguyên dương thì m – n > 0 hay m > n.

Do đó m ∈ ℕ, n ∈ ℕ sao cho m > n.

b) Gọi hai lũy thừa của x cùng bậc là x^m và x^m (m ∈ ℕ).

Khi đó thương hai lũy thừa của x cùng bậc là: x^m : x^m = 1.

Vậy thương hai lũy thừa của x cùng bậc bằng 1.

Luyện tập 1 trang 40 Toán 7 Tập 2:

Thực hiện các phép chia sau:

a) 3x⁷ : $\frac{1}{2}$x⁴; b) (-2x) : x; c) 0,25x⁵ : (-5x²).

Lời giải:

a) 3x⁷ : $\frac{1}{2}$x⁴ = $\left(3:\frac{1}{2}\right)$ . (x⁷ : x⁴) = 3 . 2 . x^7-4 = 6x³.

b) (-2x) : x = -2. (x : x) = -2.

c) 0,25x⁵ : (-5x²) = [0,25 : (-5)]. (x⁵ : x²) = – 0,05x³.

Giải Toán 7 trang 41 Tập 2

Câu hỏi trang 41 Toán 7 Tập 2:

Kiểm tra lại rằng ta có phép chia hết A : B = 2x² – 5x + 1, nghĩa là xảy ra:

A = B . (2x² – 5x + 1).

Lời giải:

Ta có B . (2x² – 5x + 1)

= (x² – 4x – 3) . (2x² – 5x + 1)

= x² . (2x² – 5x + 1) + (-4x) . (2x² – 5x + 1) – 3 . (2x² – 5x + 1)

= (x² . 2x² – x² . 5x + x² . 1) + [(–4x) . 2x² – (–4x) . 5x + (–4x) . 1]

        – (3 . 2x² – 3 . 5x + 3 . 1)

= (2x⁴ – 5x³ + x²) + (– 8x³ + 20x² – 4x) – (6x² – 15x + 3)

= 2x⁴ – 5x³ + x² – 8x³ + 20x² – 4x – 6x² + 15x – 3

= 2x⁴ + (– 5x³ – 8x³) + (x² + 20x² – 6x²) + (– 4x + 15x) – 3

= 2x⁴ – 13x³ + 15x² + 11x – 3

= A.

Vậy ta có phép chia hết A : B = 2x² – 5x + 1.

Luyện tập 2 trang 41 Toán 7 Tập 2:

Thực hiện phép chia:

a) (-x⁶ + 5x⁴ – 2x³) : 0,5x².

b) (9x² – 4) : (3x + 2).

Lời giải:

a) (-x⁶ + 5x⁴ – 2x³) : 0,5x²

= (-x⁶ : 0,5x²) + (5x⁴ : 0,5x²) + [(-2x³) : 0,5x²]

= (-1 : 0,5) . (x⁶ : x²) + (5 : 0,5) . (x⁴ : x²) + (-2 : 0,5) . (x³ : x²)

= – 2x⁴ + 10x² – 4x

b) Ta đặt tính chia như sau:

Vậy (9x² – 4) : (3x + 2) = 3x – 2.

Vận dụng trang 41 Toán 7 Tập 2:

Em hãy giải bài toán trong tình huống mở đầu.

Lời giải:

Thực hiện theo các bước sau:

Bước 1: Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B:

2x⁴ : x² = 2x².

Bước 2: Lấy A trừ đi tích B . 2x² ta được dư thứ nhất là -3x³ + x² + 6x – 2.

Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B:

(-3x³) : x² = -3x.

Bước 4: Lấy dư thứ nhất trừ đi tích B . (-3x) ta được dư thứ hai là x² – 2.

Bước 5: Lấy hạng tử bậc cao nhất của dư thứ hai chia cho hạng tử bậc cao nhất của B:

x² : x² = 1.

Bước 6: Lấy dư thứ hai trừ đi tích B . 1 ta được dư thứ ba là 0.

Dư cuối cùng bằng 0 nên quá trình chia kết thúc.

Vậy A : B = 2x² – 3x + 1.

Giải Toán 7 trang 42 Tập 2

HĐ 3 trang 42 Toán 7 Tập 2:

Bốn bước đầu tiên khi chia đa thức D = 5x³ – 3x² – x + 7 cho đa thức E = x² + 1 được viết gọn như sau:

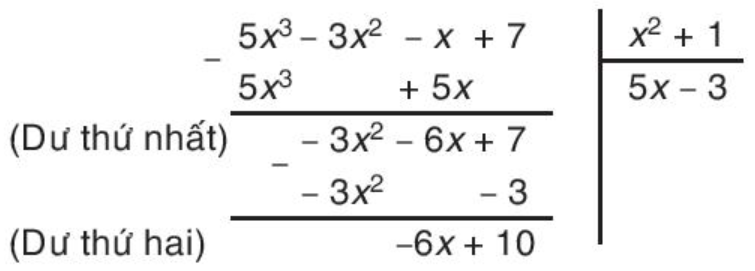
Hãy mô tả lại các bước đã thực hiện trong phép chia đa thức D cho đa thức E.

Lời giải:

Thực hiện theo các bước sau:

Bước 1. Lấy hạng tử bậc cao nhất của đa thức D chia cho hạng tử bậc cao nhất của đa thức E.

5x³ : x² = 5x.

Bước 2. Lấy D trừ đi tích E . 5x ta được dư thứ nhất là -3x² – 6x + 7.

Bước 3. Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của đa thức E.

-3x² : x² = -3.

Bước 4. Lấy dư thứ nhất trừ đi tích E . (-3) ta được dư thứ hai là -6x + 10.

Bước 5. Đa thức -6x + 10 có bậc 1, đa thức E có bậc 2 nên phép chia dừng.

HĐ 4 trang 42 Toán 7 Tập 2:

Bốn bước đầu tiên khi chia đa thức D = 5x³ – 3x² – x + 7 cho đa thức E = x² + 1 được viết gọn như sau:

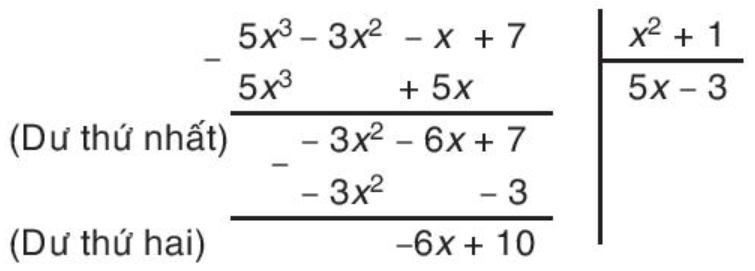
Kí hiệu dư thứ hai là G = -6x + 10. Đa thức này có bậc bằng 1. Lúc này phép chia có thể tiếp tục được không? Vì sao?

Lời giải:

Để thực hiện phép chia thì bậc của đa thức bị chia phải lớn hơn hoặc bằng bậc của đa thức chia.

Ta thấy bậc của đa thức dư G bằng 1, bậc của đa thức chia E bằng 2.

Do 1 < 2 nên phép chia không thể tiếp tục.

HĐ 5 trang 42 Toán 7 Tập 2:

Bốn bước đầu tiên khi chia đa thức D = 5x³ – 3x² – x + 7 cho đa thức E = x² + 1 được viết gọn như sau:

Hãy kiểm tra lại đẳng thức: D = E . (5x – 3) + G.

Lời giải:

Ta có E . (5x – 3) + G

= (x² + 1) . (5x – 3) + (-6x + 10)

= x² . (5x – 3) + 1 . (5x – 3) – 6x + 10

= (x² . 5x – 3 . x²) + (1 . 5x – 1 . 3) – 6x + 10

= (5x³ – 3x²) + (5x – 3) – 6x + 10

= 5x³ – 3x² + 5x – 3 – 6x + 10

= 5x³ – 3x² + (5x – 6x) + (-3 + 10)

= 5x³ – 3x² – x + 7

= D.

Vậy D = E . (5x – 3) + G.

Luyện tập 3 trang 42 Toán 7 Tập 2:

Tìm dư R và thương Q trong phép chia đa thức A = 3x⁴ – 6x – 5 cho đa thức

B = x² + 3x – 1 rồi viết A dưới dạng A = B . Q + R.

Lời giải:

Thực hiện phép chia ta được:

Do đó dư R bằng -105x + 25; thương Q bằng 3x² – 9x + 30.

Vậy 3x⁴ – 6x – 5 = (x² + 3x – 1) . (3x² – 9x + 30) – 105x + 25.

Thử thách nhỏ trang 42 Toán 7 Tập 2:

Tròn: “Đố Vuông tìm được dư trong phép chia x³ – 3x² + x – 1 cho x² – 3x”.

Vuông: “Mình chỉ nhìn qua cũng biết được dư là x – 1”.

Em có biết tại sao Vuông làm nhanh thế không?

Lời giải:

Ta có: x³ – 3x² + x – 1 = (x³ – 3x²) + (x – 1) = x(x² – 3x) + (x – 1).

Đa thức x³ – 3x² chia cho đa thức x² – 3x được kết quả là x, dư 0.

Nên dư của phép chia đa thức x³ – 3x² + x – 1 cho đa thức x² – 3x là dư của phép chia đa thức x – 1 cho đa thức x² – 3x.

Bậc của đa thức x – 1 là 1, bậc của đa thức x² – 3x là 2 nên không thể thực hiện phép chia.

Do đó dư của phép chia x³ – 3x² + x – 1 cho x² – 3x bằng x – 1.

B. Bài tập

Giải Toán 7 trang 43 Tập 2

Bài 7.30 trang 43 Toán 7 Tập 2:

Tính:

a) 8x⁵ : 4x³; b) 120x⁷ : (-24x⁵);

c) $\frac{3}{4}$(-x)³ : $\frac{1}{8}$x d) -3,72x⁴ : (-4x²).

Lời giải:

a) 8x⁵ : 4x³ = (8 : 4) . (x⁵ : x³) = 2x².

b) 120x⁷ : (-24x⁵) = [120 : (-24)] . (x⁷ : x⁵) = -5x².

c) $\frac{3}{4}$(-x)³ : $\frac{1}{8}$x = $\frac{3}{4}$. (-x³) : $\frac{1}{8}$x = $\left(\frac{-3}{4}:\frac{1}{8}\right)$ . (x³ : x) = $\left(\frac{-3}{4}.8\right)$x^3-1 = – 6x².

d) -3,72x⁴ : (-4x²) = [(-3,72) : (-4)] . (x⁴ : x²) = 0,93x².

Bài 7.31 trang 43 Toán 7 Tập 2:

Thực hiện các phép chia đa thức sau:

a) (-5x³ + 15x² + 18x) : (-5x);

b) (-2x⁵ – 4x³ + 3x²) : 2x².

Lời giải:

a) (-5x³ + 15x² + 18x) : (-5x)

= (-5x³) : (-5x) + 15x² : (-5x) + 18x : (-5x)

= [(-5) : (-5)] . (x³ : x) + [15 : (-5)] . (x² : x) + [18 : (-5)] . (x : x)

= x² + (-3)x + (– 3,6)

= x² – 3x – 3,6

b) (-2x⁵ – 4x³ + 3x²) : 2x²

= (-2x⁵) : 2x² + (-4x³) : 2x² + 3x² : 2x²

= (-2 : 2) . (x⁵ : x²) + (-4 : 2) . (x³ : x²) + (3 : 2) . (x² : x²)

= -x³ + (-2)x + 1,5

= -x³ – 2x + 1,5

Bài 7.32 trang 43 Toán 7 Tập 2:

Thực hiện các phép chia đa thức sau bằng cách đặt tính chia:

a) (6x³ – 2x² – 9x + 3) : (3x – 1);

b) (4x⁴ + 14x³ – 21x – 9) : (2x² – 3).

Lời giải:

a) Đặt tính chia như sau:

Vậy (6x³ – 2x² – 9x + 3) : (3x – 1) = 2x² – 3.

b) Đặt tính chia như sau:

Vậy (4x⁴ + 14x³ – 21x – 9) : (2x² – 3) = 2x² + 7x + 3.

Bài 7.33 trang 43 Toán 7 Tập 2:

Thực hiện phép chia 0,5x⁵ + 3,2x³ – 2x² cho 0,25xⁿ trong mỗi trường hợp sau:

a) n = 2;

b) n = 3.

Lời giải:

a) Với n = 2 ta có

(0,5x⁵ + 3,2x³ – 2x²) : 0,25x²

= 0,5x⁵ : 0,25x² + 3,2x³ : 0,25x² + (-2x²) : 0,25x²

= (0,5 : 0,25) . (x⁵ : x²) + (3,2 : 0,25) . (x³ : x²) + (-2 : 0,25) . (x² : x²)

= 2x³ + 12,8x – 8

b) Với n = 3 thì đa thức chia 0,25x³ có bậc bằng 3.

Trong đa thức bị chia 0,5x⁵ + 3,2x³ – 2x² có hạng tử -2x² có bậc bằng 2 < 3 nên ta thực hiện đặt tính chia:

Vậy 0,5x⁵ + 3,2x³ – 2x² = 0,25x³ . (2x² + 12,8) – 2x².

Bài 7.34 trang 43 Toán 7 Tập 2:

Trong mỗi trường hợp sau đây, tìm thương Q(x) và dư R(x) trong phép chia F(x) cho G(x) rồi biểu diễn F(x) dưới dạng:

F(x) = G(x) . Q(x) + R(x).

a) F(x) = 6x⁴ – 3x³ + 15x² + 2x – 1; G(x) = 3x².

b) F(x) = 12x⁴ + 10x³ – x – 3; G(x) = 3x² + x + 1.

Lời giải:

a) Đặt tính chia như sau:

Do đó Q(x) = 2x² – x + 5; R(x) = 2x – 1.

Vậy 6x⁴ – 3x³ + 15x² + 2x – 1 = 3x² . (2x² – x + 5) + 2x – 1.

b) Đặt tính chia như sau:

Do đó Q(x) = 4x² + 2x – 2; R(x) = -x – 1.

Vậy 12x⁴ + 10x³ – x – 3 = (3x² + x + 1) . (4x² + 2x – 2) – x – 1.

Bài 7.35 trang 43 Toán 7 Tập 2:

Bạn Tâm lúng túng khi muốn tìm thương và dư trong phép chia đa thức 21x – 4 cho 3x².

Em có thể giúp bạn Tâm được không?

Lời giải:

Ta thấy bậc của đa thức bị chia 21x – 4 (là 1) nhỏ hơn bậc của đa thức chia 3x² (là 2).

Do đó không thể thực hiện được phép chia.

Vậy thương của phép chia bằng 0 và dư của phép chia là 21x – 4.

Xem thêm các bài giải sách giáo khoa Toán 7 bộ sách Kết nối tri thức hay, chi tiết khác:

Luyện tập chung trang 45

Bài tập cuối chương 7

Bài 29: Làm quen với biến cố

Bài 30: Làm quen với xác suất của biến cố

Luyện tập chung trang 57

Đăng bởi: THCS Bình Chánh

Chuyên mục: Giải Toán 7 Kết nối tri thức

• Giải Bài 9.29 trang 81 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
• Giải Bài 9.30 trang 81 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
• Giải Bài 6.33 trang 21 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
• Giải Bài 6.27 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
• Giải Bài 6.28 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
• Giải Bài 6.29 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống