Giải Toán 7 Bài 4 Cánh diều: Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh

Mời các em theo dõi nội dung bài học do thầy cô trường Trung học Bình Chánh biên soạn sẽ giúp các em nắm chắc kiến thức nội dung bài học tốt hơn.

Giải bài tập Toán 7 Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh

A. Câu hỏi trong bài

Giải Toán 7 trang 80 Tập 2

Câu hỏi khởi động trang 80 Toán 7 Tập 2: Giá để đồ ở Hình 33 gợi nên hình ảnh hai tam giác ABC và A’B’C’ có: AB = A’B’; BC = B’C’; CA = C’A’.

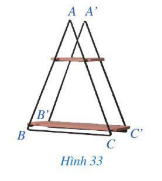
Tam giác ABC có bằng tam giác A’B’C’ hay không?

Lời giải

Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

Xét tam giác ABC và tam giác A’B’C’ có:

AB = A’B’; BC = B’C’; CA = C’A’ (giả thiết)

Suy ra ∆ABC = ∆A’B’C’ (c.c.c)

Vậy ∆ABC = ∆A’B’C’.

Hoạt động 1 trang 80 Toán 7 Tập 2: Cho hai tam giác ABC và A’B’C’ (Hình 34) có: AB = A’B’ = 2 cm, AC = A’C’ = 3 cm, BC = B’C’ = 4 cm.

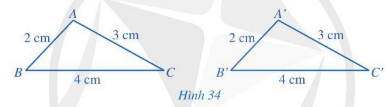
Hãy sử dụng thước đo góc để kiểm nghiệm rằng: $\hat{A} = \hat{A^{‘}};$ $\hat{B} = \hat{B^{‘}};$ $\hat{C} = \hat{C^{‘}} .$

Lời giải

Dùng thước đo góc ta đo được:

+ Trong tam giác ABC: $\hat{A} \approx 104 °,$ $\hat{B} \approx 47 °, \hat{C} \approx 29 °$

+ Trong tam giác A’B’C’: $\hat{A^{‘}} \approx 104 °,$ $\hat{B^{‘}} \approx 47 °, \hat{C^{‘}} \approx 29 °$

Vậy $\hat{A} = \hat{A^{‘}};$ $\hat{B} = \hat{B^{‘}};$ $\hat{C} = \hat{C^{‘}} .$

Giải Toán 7 trang 81 Tập 2

Luyện tập 1 trang 81 Toán 7 Tập 2: Hai tam giác ở Hình 37 có bằng nhau không? Vì sao?

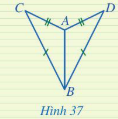
Lời giải

$∆$ ABC, M ∈ BC

∆AMB = ∆AMC.

a) M là trung điểm của BC;

b) Tia AM là tia phân giác của góc BAC và $A M ⊥ B C .$

Chứng minh (Hình 37):

Xét tam giác ABC và tam giác ABD có:

AB là cạnh chung; AC = AD; BC = BD

Suy ra ∆ABC = ∆ABD (c.c.c)

Vậy ∆ABC = ∆ABD.

Giải Toán 7 trang 82 Tập 2

Hoạt động 2 trang 82 Toán 7 Tập 2: Cho hai tam giác vuông ABC và A’B’C’ có: $\hat{A} = \hat{A^{‘}} = 90 °,$ AB = A’B’ = 3 cm, BC = B’C’ = 5 cm (Hình 39). So sánh độ dài các cạnh AC và A’C’.

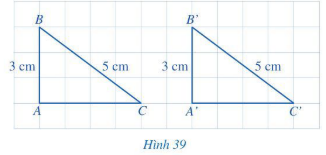
Lời giải

Giả sử cạnh hình vuông nhỏ trong hình vẽ có độ dài bằng a (cm).

Quan sát hình vẽ ta thấy: Cạnh AB và cạnh A’B’ có độ dài bằng 3 lần độ dài của cạnh hình vuông.

Mà AB = A’B’ = 3 cm nên 3a = 3 suy ra a = 1 (cm)

Lại có AC = 4a = 4.1 = 4 (cm) và A’C’ = 4a = 4.1 = 4 (cm)

Do đó AC = A’C’ (= 4cm)

Vậy AC = A’C’.

B. Bài tập

Giải Toán 7 trang 83 Tập 2

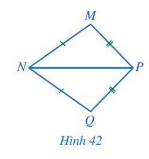
Bài 1 trang 83 Toán 7 Tập 2: Cho Hình 42 có MN = QN, MP = QP. Chứng minh rằng $\hat{M N P} = \hat{Q N P} .$

Lời giải

$∆$ MNP, ∆QNP

MN = QN, MP = QP

$\hat{M N P} = \hat{Q N P} .$

Chứng minh (Hình 42):

Xét tam giác MNP và tam giác QNP có:

MN = QN (giả thiết); MP = QP (giả thiết); NP là cạnh chung.

Suy ra $∆$ MNP = $∆$ QNP (c.c.c)

Do đó $\hat{M N P} = \hat{Q N P}$ (hai góc tương ứng)

Vậy $\hat{M N P} = \hat{Q N P}$

Bài 2 trang 83 Toán 7 Tập 2:

Cho Hình 43 có AB = AD, $\hat{A B C} = \hat{A D C} = 90 ° .$ Chứng minh $\hat{A C B} = \hat{A C D} .$

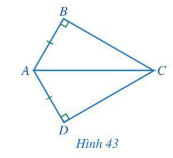
Lời giải

$∆$ ABC, ∆ADC

AB = AD

$\hat{A B C} = \hat{A D C} = 90 ° .$

$\hat{A C B} = \hat{A C D} .$

Chứng minh (Hình 43):

Vì $∆$ ABC có $\hat{A B C} = 90 °$ (giả thiết) nên $∆$ ABC vuông tại B.

Vì ∆ADC có $\hat{A D C} = 90 °$ (giả thiết) nên ∆ADC vuông tại D.

Xét hai tam giác ABC (vuông tại B) và tam giác ADC (vuông tại D) có:

AC là cạnh chung

AB = AD (giả thiết)

Suy ra $∆$ ABC = ∆ADC (cạnh huyền – cạnh góc vuông)

Do đó $\hat{A C B} = \hat{A C D}$ (hai góc tương ứng)

Vậy $\hat{A C B} = \hat{A C D}$

Bài 3 trang 83 Toán 7 Tập 2:

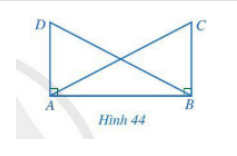
Cho Hình 44 có AC = BD, $\hat{A B C} = \hat{B A D} = 90 ° .$ Chứng minh AD = BC.

Lời giải

$∆$ ABC, ∆ABD

AC = BD, $\hat{A B C} = \hat{B A D} = 90 ° .$

AD = BC

Chứng minh (Hình 44):

Vì $\hat{A B C} = \hat{B A D} = 90 °$ nên $∆$ ABC vuông tại B và $∆$ ABD vuông tại A.

Xét tam giác ABC (vuông tại B) và tam giác BAD (vuông tại A) có:

AB là cạnh chung

AC = BD (giả thiết)

Suy ra $∆$ ABC = $∆$ BAD (cạnh huyền – cạnh góc vuông)

Do đó BC = AD (hai cạnh tương ứng)

Vậy BC = AD.

Bài 4 trang 83 Toán 7 Tập 2: Cho hai tam giác ABC và MNP thoả mãn: AB = MN, BC = NP, AC = MP, $\hat{A} = 65 °, \hat{N} = 71 ° .$ Tính số đo các góc còn lại của hai tam giác.

Lời giải

$∆$ ABC, ∆MNP

AB = MN, BC = NP, AC = MP; $\hat{A} = 65 °, \hat{N} = 71 ° .$

Tính số đo của $\hat{B}, \hat{C}, \hat{M}, \hat{P} .$

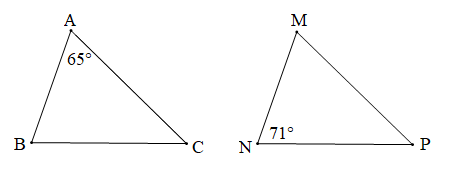
Xét tam giác ABC và tam giác MNP có:

AB = MN (giả thiết)

BC = NP (giả thiết)

AC = MP (giả thiết)

Suy ra ∆ABC = ∆MNP (c.c.c)

Nên $\hat{A} = \hat{M}, \hat{B} = \hat{N}, \hat{C} = \hat{P}$ (các cặp góc tương ứng)

Mà $\hat{A} = 65 °, \hat{N} = 71 °$ (giả thiết)

Do đó $\hat{M} = 65 °, \hat{B} = 71 °$

Xét tam giác ABC với $\hat{A} = 65 °,$ $\hat{B} = 71 °$ ta có:

$\hat{A} + \hat{B} + \hat{C} = 180 °$ (tổng ba góc trong một tam giác)

Suy ra $\hat{C} = 180 ° - \hat{A} - \hat{B}$

Hay $\hat{C} = 180 ° - 65 ° - 71 ° = 44 °$

Suy ra $\hat{P} = 44 °$

Vậy $\hat{M} = 65 °, \hat{B} = 71 °, \hat{C} = 44 °$ và $\hat{P} = 44 ° .$

Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 5: Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh

Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc

Bài 7: Tam giác cân

Bài 8: Đường vuông góc và đường xiên

Bài 9: Đường trung trực của một đoạn thẳng

Đăng bởi: THCS Bình Chánh

Chuyên mục: Toán 7 Cánh Diều

Rate this post

Sign up for Newsletter

Học Tập, Lớp 7, Toán 7 Cánh Diều

Giải Toán 7 Bài 4 Cánh diều: Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh

Trường THCS Bình Chánh

Trả lời Hủy