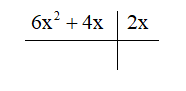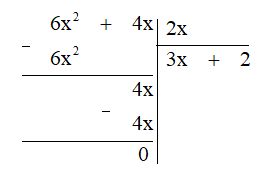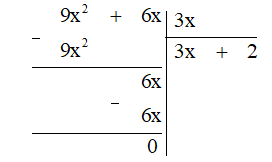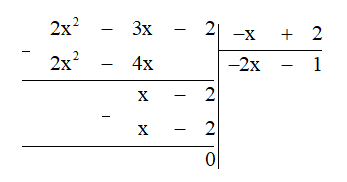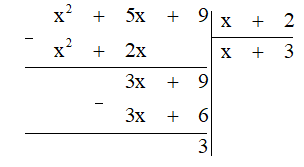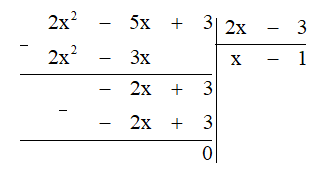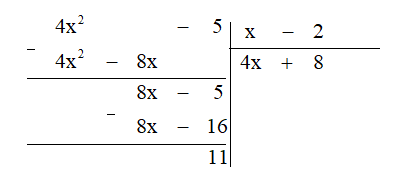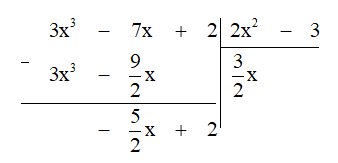Giải Toán 7 Bài 4 Chân trời sáng tạo: Phép nhân và phép chia đa thức một biến
Mời các em theo dõi nội dung bài học do thầy cô trường Trung học Bình Chánh biên soạn sẽ giúp các em nắm chắc kiến thức nội dung bài học tốt hơn.
Giải bài tập Toán 7 Bài 4: Phép nhân và phép chia đa thức một biến
Giải Toán 7 trang 37 Tập 2
Bạn đang xem: Giải Toán 7 Bài 4 Chân trời sáng tạo: Phép nhân và phép chia đa thức một biến
Khởi động trang 37 Toán 7 Tập 2:
Có thể nhân, chia hai đa thức một biến được không?
Lời giải:
Ta có thể thực hiện nhân, chia hai đa thức một biến.
Khám phá 1 trang 37 Toán 7 Tập 2:
Hãy dùng tính chất phân phối để thực hiện phép nhân x . (2x + 3).
Lời giải:
Áp dụng tính chất phân phối, ta được:
x . (2x + 3) = x . 2x + x . 3 = 2x2 + 3x.
Thực hành 1 trang 37 Toán 7 Tập 2:
Thực hiện phép nhân (4x – 3)(2x2 + 5x – 6).
Lời giải:
Ta có: (4x – 3)(2x2 + 5x – 6)
= 4x . (2x2 + 5x – 6) + (-3) . (2x2 + 5x – 6)
= 4x . 2x2 + 4x . 5x + 4x . (-6) + (-3) . 2x2 + (-3) . 5x + (-3) . (-6)
= 8x3 + 20x2 – 24x – 6x2 – 15x + 18
= 8x3 + (20x2 – 6x2) + (-24x – 15x) + 18
= 8x3 + 14x2 – 39x + 18.
Vậy (4x – 3)(2x2 + 5x – 6) = 8x3 + 14x2 – 39x + 18.
Vận dụng 1 trang 37 Toán 7 Tập 2:
Tìm đa thức theo biến x biểu thị thể tích của hình hộp chữ nhật có kích thước như Hình 2.
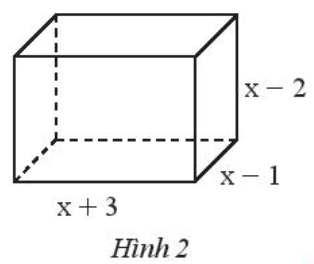
Lời giải:
Biểu thức biểu thị thể tích của hình hộp chữ nhật trên là:
(x + 3)(x – 1)(x – 2)
= [x . x + 3 . x + x . (-1) + 3 . (-1)] . (x – 2)
= (x2 + 3x – x – 3) . (x – 2)
= (x2 + 2x – 3) . (x – 2)
= x2 . x + x2 . (-2) + 2x . x + 2x . (-2) + (-3) . x + (-3) . (-2)
= x3 – 2x2 + 2x2 – 4x – 3x + 6
= x3 + (-2x2 + 2x2) + (-4x – 3x) + 6
= x3 – 7x + 6.
Vậy đa thức biểu thị thể tích của hình hộp chữ nhật trên là x3 – 7x + 6.
Giải Toán 7 trang 38 Tập 2
Khám phá 2 trang 38 Toán 7 Tập 2:
Thực hiện phép nhân (3x + 1)(x2 – 2x + 1),
rồi đoán xem (3x3 – 5x2 + x + 1) : (3x + 1) bằng đa thức nào.
Lời giải:
(3x + 1)(x2 – 2x + 1) = 3x . (x2 – 2x + 1) + 1 . (x2 – 2x + 1)
= 3x . x2 + 3x . (-2x) + 3x . 1 + x2 – 2x + 1
= 3x3 – 6x2 + 3x + x2 – 2x + 1
= 3x3 + (-6x2 + x2) + (3x – 2x) + 1
= 3x3 – 5x2 + x + 1.
Khi đó (3x3 – 5x2 + x + 1) : (3x + 1) = x2 – 2x + 1.
Thực hành 2 trang 38 Toán 7 Tập 2:
Thực hiện phép chia P(x) = 6x2 + 4x cho Q(x) = 2x.
Lời giải:
Thực hiện theo các bước như sau:
– Đặt phép chia
– Lấy hạng tử bậc cao nhất của đa thức P(x) chia cho hạng tử bậc cao nhất của đa thức Q(x) được 6x2 : 2x = 3x.
– Lấy P(x) trừ 3x . Q(x) ta được dư thứ nhất: 3x . 2x = 6x2.
– Lấy đa thức bị chia trừ 6x2, ta được:
Đa thức 4x là dư thứ nhất.
– Chia hạng tử bậc cao nhất của dư thứ nhất cho hạng tử bậc cao nhất của đa thức Q(x) được 4x : 2x = 2.
– Lấy dư thứ nhất trừ đi 2 . Q(x) ta được dư thứ hai: 4x – 2 . 2x = 4x – 4x = 0.
Do dư bằng 0 nên dừng phép chia.
Vậy P(x) : Q(x) = 3x + 2.
Giải Toán 7 trang 39 Tập 2
Vận dụng 2 trang 39 Toán 7 Tập 2:
Thực hiện các phép chia sau: và .
Lời giải:
* Xét :
Ta có 9x2 + 5x + x = 9x2 + 6x.
Thực hiện đặt phép chia, ta được:
Do đó = 3x + 2.
* Xét :
Ta có 2 – x = -x + 2.
Thực hiện đặt phép chia ta được:
Do đó = -2x – 1.
Vậy = 3x + 2 và = -2x – 1.
Thực hành 3 trang 39 Toán 7 Tập 2:
Thực hiện phép chia (x2 + 5x + 9) : (x + 2).
Lời giải:
Thực hiện đặt phép chia, ta được:
Vậy .
Vận dụng 3 trang 39 Toán 7 Tập 2:
Tính diện tích đáy của một hình hộp chữ nhật (Hình 3) có chiều cao bằng (x + 3) cm và có thể tích bằng (x3 + 8x2 + 19x + 12) cm3.
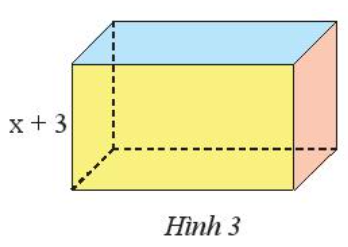
Lời giải:
Ta có công thức tính thể tích hình hộp chữ nhật là:
V = S . h (trong đó V, S và h lần lượt là thể tích, diện tích đáy và chiều cao hình hộp chữ nhật).
Khi đó, diện tích đáy hình hộp chữ nhật là:
S = V : h = (x3 + 8x2 + 19x + 12) : (x + 3) = x2 + 5x + 4 (cm2).
Vậy diện tích đáy của hình hộp chữ nhật bằng (x2 + 5x + 4) cm2.
Giải Toán 7 trang 40 Tập 2
Thực hành 4 trang 40 Toán 7 Tập 2:
Thực hiện phép tính: . (x2 + 1) . 5.
Lời giải:
Cách 1: Thực hiện từ trái sang phải.
. (x2 + 1) . 5 =
= = x2 + 1.
Cách 2: Sử dụng tính chất giao hoán và kết hợp để tính giá trị biểu thức.
. (x2 + 1) . 5 = . 5 . (x2 + 1)
= . (x2 + 1) = x2 + 1.
Bài 1 trang 40 Toán 7 Tập 2: Thực hiện phép nhân.
a) (4x – 3)(x + 2);
b) (5x + 2)(-x2 + 3x + 1);
c) (2x2 – 7x + 4)(-3x2 + 6x + 5).
Lời giải:
a) (4x – 3)(x + 2)
= 4x . x + 4x . 2 + (-3) . x + (-3) . 2
= 4x2 + 8x – 3x – 6
= 4x2 + (8x – 3x) – 6
= 4x2 + 5x – 6.
b) (5x + 2)(-x2 + 3x + 1)
= 5x . (-x2) + 5x . 3x + 5x . 1 + 2 . (-x2) + 2 . 3x + 2 . 1
= -5x3 + 15x2 + 5x – 2x2 + 6x + 2
= -5x3 + (15x2 – 2x2) + (5x + 6x) + 2
= -5x3 + 13x2 + 11x + 2.
c) (2x2 – 7x + 4)(-3x2 + 6x + 5)
= 2x2 . (-3x2) + 2x2 . 6x + 2x2 . 5 + (-7x) . (-3x2) + (-7x) . 6x + (-7x) . 5 + 4 . (-3x2) + 4 . 6x + 4 . 5
= -6x4 + 12x3 + 10x2 + 21x3 – 42x2 – 35x – 12x2 + 24x + 20
= -6x4 + (12x3 + 21x3) + (10x2 – 42x2 – 12x2) + (-35x + 24x) + 20
= -6x4 + 33x3 – 44x2 – 11x + 20.
Bài 2 trang 40 Toán 7 Tập 2:
Cho hai hình chữ nhật như Hình 4. Tìm đa thức theo biến x biểu thị diện tích của phần được tô màu xanh.

Lời giải:
∙ Hình chữ nhật bên ngoài có chiều dài là 2x + 4 và chiều rộng là 3x + 2.
Khi đó, biểu thức biểu thị diện tích của hình chữ nhật bên ngoài là:
(2x + 4)(3x + 2) = 6x2 + 4x + 12x + 8 = 6x2 + 16x + 8.
∙ Hình chữ nhật bên trong có chiều dài là x + 1 và chiều rộng là x.
Khi đó, biểu thức biểu thị diện tích của hình chữ nhật bên trong là:
x . (x + 1) = x2 + x.
Do đó biểu thức biểu thị diện tích của phần được tô màu xanh là:
(6x2 + 16x + 8) – (x2 + x)
= 6x2 + 16x + 8 – x2 – x
= (6x2 – x2) + (16x – x) + 8
= 5x2 + 15x + 8.
Vậy biểu thức biểu thị diện tích của phần được tô màu xanh là 5x2 + 15x + 8.
Bài 3 trang 40 Toán 7 Tập 2: Thực hiện phép chia.
a) (8x6 – 4x5 + 12x4 – 20x3) : 4x3;
b) (2x2 – 5x + 3) : (2x – 3).
Lời giải:
a) Ta có (8x6 – 4x5 + 12x4 – 20x3) : 4x3
= (8x6 : 4x3) + (-4x5 : 4x3) + (12x4 : 4x3) + (-20x3) : 4x3
= 2x3 – x2 + 3x – 5
Vậy (8x6 – 4x5 + 12x4 – 20x3) : 4x3 = 2x3 – x2 + 3x – 5.
b) Thực hiện đặt phép chia, ta được:
Vậy (2x2 – 5x + 3) : (2x – 3) = x – 1.
Bài 4 trang 40 Toán 7 Tập 2: Thực hiện phép chia.
a) (4x2 – 5) : (x – 2);
b) (3x3 – 7x + 2) : (2x2 – 3).
Lời giải:
a) Thực hiện đặt phép chia ta được:
Vậy .
b) Thực hiện đặt phép chia ta được:
Vậy .
Bài 5 trang 40 Toán 7 Tập 2:
Tính chiều dài của một hình chữ nhật có diện tích bằng (4y2 + 4y – 3) cm2 và chiều rộng bằng (2y – 1) cm.
Lời giải:
Chiều dài của hình chữ nhật là:
(4y2 + 4y – 3) : (2y – 1) = 2y + 3 (cm)
Vậy chiều dài của hình chữ nhật đó bằng (2y + 3) cm.
Bài 6 trang 40 Toán 7 Tập 2:
Cho hình hộp chữ nhật có thể tích bằng (3x3 + 8x2 – 45x – 50) cm3, chiều dài bằng
(x + 5) cm và chiều cao bằng (x + 1) cm. Hãy tính chiều rộng của hình hộp chữ nhật đó.
Lời giải:
Diện tích đáy của hình hộp chữ nhật là:
(3x3 + 8x2 – 45x – 50) : (x + 1) = 3x2 + 5x – 50 (cm)
Chiều rộng của hình hộp chữ nhật là:
(3x2 + 5x – 50) : (x + 5) = 3x – 10 (cm)
Vậy chiều rộng của hình hộp chữ nhật bằng (3x – 10) cm.
Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Phép cộng và phép trừ đa thức một biến
Bài 4: Phép nhân và phép chia đa thức một biến
Bài 5: Hoạt động thực hành và trải nghiệm. Cách tính điểm trung bình môn học kì
Bài tập cuối chương 7
Bài 1: Góc và cạnh của một tam giác
Đăng bởi: THCS Bình Chánh
Chuyên mục: Toán 7 Chân trời sáng tạo
- Giải Bài 9.29 trang 81 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 9.30 trang 81 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.33 trang 21 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.27 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.28 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.29 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống