Giải Toán 7 Bài 9 Cánh diều: Đường trung trực của một đoạn thẳng
Mời các em theo dõi nội dung bài học do thầy cô trường Trung học Bình Chánh biên soạn sẽ giúp các em nắm chắc kiến thức nội dung bài học tốt hơn.
Giải bài tập Toán 7 Bài 9: Đường trung trực của một đoạn thẳng
A. Câu hỏi trong bài
Bạn đang xem: Giải Toán 7 Bài 9 Cánh diều: Đường trung trực của một đoạn thẳng
Giải Toán 7 trang 100 Tập 2
Câu hỏi khởi động trang 100 Toán 7 Tập 2: Hình 86 minh họa chiếc cân thăng bằng và gợi nên hình ảnh đoạn thẳng AB, đường thẳng d.

Đường thẳng d có mối liên hệ gì với đoạn thẳng AB?
Lời giải:
Khi chiếc cân thăng bằng thì đường thẳng d vuông góc với đoạn thẳng AB tại trung điểm của AB.
Hoạt động 1 trang 100 Toán 7 Tập 2: Quan sát Hình 87.
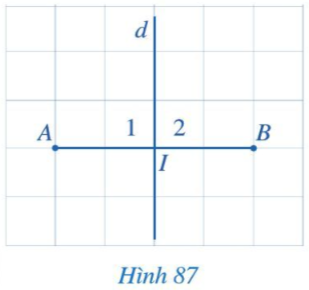
a) So sánh hai đoạn thẳng IA và IB.
b) Tìm số đo của các góc I1, I2.
Lời giải:
a) Ta coi độ dài cạnh ô vuông nhỏ bằng 1 đơn vị.
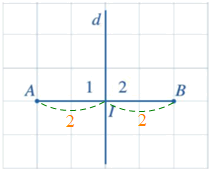
Khi đó IA = 2 và IB = 2.
Do đó IA = IB.
b) Ta thấy đường thẳng d vuông góc với AB nên .
Giải Toán 7 trang 101 Tập 2
Luyện tập 1 trang 101 Toán 7 Tập 2:
Cho tam giác ABC và M là trung điểm của BC. Biết . Chứng minh AM là đường trung trực của đoạn thẳng BC.
Lời giải:
|
GT |
ABC, M là trung điểm của BC, |
|
KL |
AM là đường trung trực của đoạn thẳng BC. |
Chứng minh (Hình vẽ dưới đây):
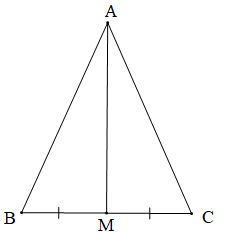
Vì và là hai góc kề bù nên (tính chất hai góc kề bù)
Mà (giả thiết) nên
Suy ra AM BC.
Lại có M là trung điểm của BC (giả thiết)
Do đó AM BC tại trung điểm M của BC nên AM là đường trung trực của BC.
Vậy AM là đường trung trực của BC.
Hoạt động 2 trang 101 Toán 7 Tập 2: Cho đoạn thẳng AB có trung điểm O, d là đường trung trực của đoạn thẳng AB, điểm M thuộc d, M khác O (Hình 90).
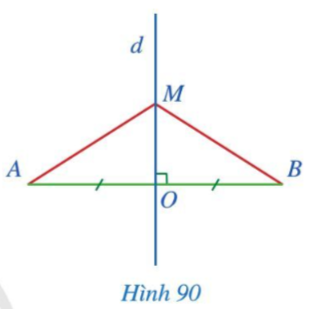
Chứng minh rằng:
a) MOA = MOB;
b) MA = MB.
Lời giải:
|
GT |
O là trung điểm của AB, d là đường trung trực của đoạn thẳng AB, M ∈ d, M ≠ O. |
|
KL |
a) MOA = MOB; b) MA = MB. |
Chứng minh (Hình 90):
a) Vì d là đường trung trực của đoạn thẳng AB (giả thiết)
Nên MO AB tại O
Do đó tam giác MOA vuông tại O và tam giác MOB vuông tại O.
Xét MOA (vuông tại O) và MOB (vuông tại O) có:
MO là cạnh chung,
OA = OB (O là trung điểm của AB).
Do đó MOA = MOB (hai cạnh góc vuông).
Vậy MOA = MOB.
b) Vì MOA = MOB (chứng minh trên)
Nên MA = MB (hai cạnh tương ứng).
Vậy MA = MB.
Luyện tập 2 trang 101 Toán 7 Tập 2: Hình 91 mô tả mặt cắt đứng của một ngôi nhà với hai mái là OA và OB, mái nhà bên trái dài 3 m. Tính chiều dài mái nhà bên phải, biết rằng điểm O thuộc đường trung trực của đoạn thẳng AB.
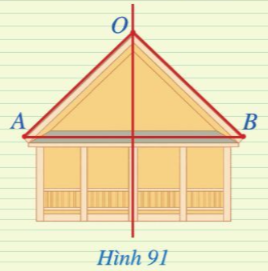
Lời giải:
Do O thuộc đường trung trực của đoạn thẳng AB nên OA = OB (tính chất đường trung trực)
Mà OA = 3 m nên OB = 3 m.
Vậy chiều dài mái nhà bên phải là 3 m.
Hoạt động 3 trang 101 Toán 7 Tập 2: Cho đoạn thẳng AB có trung điểm O. Giả sử M là một điểm khác O sao cho MA = MB.
a) Hai tam giác MOA và MOB có bằng nhau hay không? Vì sao?
b) Đường thẳng MO có là đường trung trực của đoạn thẳng AB hay không? Vì sao?
Lời giải:
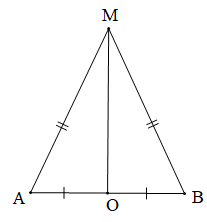
a) Xét MOA và MOB có:
OA = OB (O là trung điểm của AB),
MA = MB (giả thiết),
MO là cạnh chung
Do đó MOA = MOB (c.c.c).
Vậy MOA = MOB.
b) Vì MOA = MOB (chứng minh câu a)
Nên (hai góc tương ứng)
Mà (tính chất hai góc kề bù)
Do đó
Khi đó MO AB tại trung điểm O của đoạn thẳng AB.
Vậy MO là đường trung trực của đoạn thẳng AB.
Giải Toán 7 trang 102 Tập 2
Luyện tập 3 trang 102 Toán 7 Tập 2:
Cho tam giác ABC cân tại A.
a) Điểm A có thuộc đường trung trực của đoạn thẳng BC hay không? Vì sao?
b) Đường thẳng qua A vuông góc với BC cắt cạnh BC tại H. Đường thẳng AH có là đường trung trực của đoạn thẳng BC hay không? Vì sao?
Lời giải:
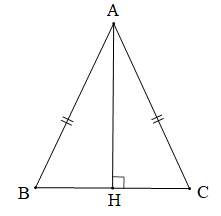
a) Tam giác ABC cân tại A (giả thiết) nên AB = AC.
Do AB = AC nên A nằm trên đường trung trực của đoạn thẳng BC.
Vậy A thuộc đường trung trực của đoạn thẳng BC.
b) Vì AH BC tại H nên ABH vuông tại H và ACH vuông tại H.
Xét ABH (vuông tại H) và ACH (vuông tại H) có:
AB = AC (chứng minh trên),
AH là cạnh chung.
Do đó ABH = ACH (cạnh huyền – cạnh góc vuông).
Suy ra HB = HC (hai cạnh tương ứng).
Mà H nằm giữa B và C nên H là trung điểm của BC.
Ta có AH vuông góc với BC tại trung điểm H của BC nên AH là đường trung trực của đoạn thẳng BC.
Vậy đường thẳng AH là đường trung trực của đoạn thẳng BC.
Hoạt động 4 trang 102 Toán 7 Tập 2: Dùng thước thẳng (có chia đơn vị) và compa vẽ đường trung trực của đoạn thẳng AB, biết AB = 3 cm.
Lời giải:
Để vẽ đường trung trực của đoạn thẳng AB, ta thực hiện theo các bước sau:
Bước 1. Vẽ đoạn thẳng AB = 3 cm.
Bước 2. Vẽ một phần đường tròn tâm A bán kính 2 cm.
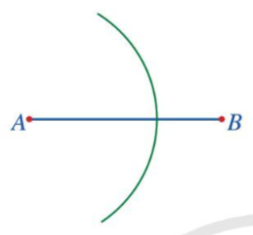
Bước 3. Vẽ một phần đường tròn tâm B bán kính 2 cm, cắt phần đường tròn tâm A vẽ ở Bước 2 tại các điểm C và D.
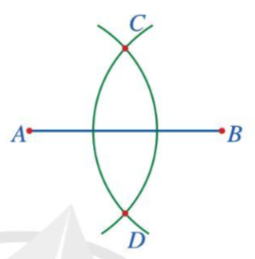
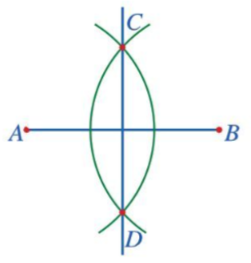
Bước 4. Vẽ đường thẳng đi qua hai điểm C và D. Đường thẳng CD là đường trung trực của đoạn thẳng AB.
B. Bài tập
Giải Toán 7 trang 103 Tập 2
Bài 1 trang 103 Toán 7 Tập 2: Trong Hình 94, đường thẳng CD là đường trung trực của đoạn thẳng AB. Chứng minh .
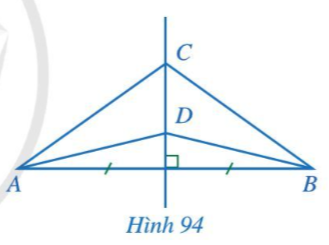
Lời giải
|
GT |
CD là đường trung trực của đoạn thẳng AB |
|
KL |
Chứng minh (Hình vẽ dưới đây):
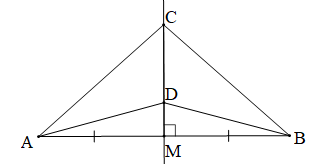
Gọi M là giao điểm của CD và AB. Khi đó M là trung điểm của AB.
CD là đường trung trực của đoạn thẳng AB nên:
+) C thuộc đường trung trực của đoạn thẳng AB do đó CA = CB.
+) D thuộc đường trung trực của đoạn thẳng AB do đó DA = DB.
Xét CAD và CBD có:
CD là cạnh chung,
CA = AB (chứng minh trên),
DA = DB (chứng minh trên)
Do đó CAD = CBD (c.c.c)
Do đó (hai góc tương ứng)
Vậy .
Bài 2 trang 103 Toán 7 Tập 2: Trong Hình 95, đường thẳng a là đường trung trực của cả hai đoạn thẳng AB và CD.
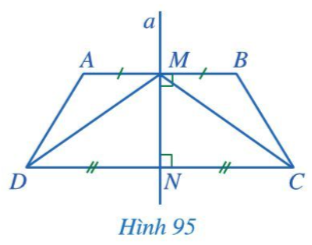
Chứng minh:
a) AB // CD;
b) MNC = MND;
c) ;
d) AD = BC, ;
e) .
Lời giải:
|
GT |
a là đường trung trực của đoạn thẳng AB và CD, M là trung điểm của AB, N là trung điểm của CD |
|
KL |
a) AB // CD; b) MNC = MND; c) ; d) AD = BC, ; e) . |
Chứng minh (Hình 95):
a) Vì a là đường trung trực của cả hai đoạn thẳng AB và CD (giả thiết)
Nên a AB và a CD.
Do đó AB // CD (hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba)
Vậy AB // CD.
b) Ta có: a CD tại N nên MNC vuông tại N và MND vuông tại N.
Xét MNC (vuông tại N) và MND (vuông tại N) có:
MN là cạnh chung
NC = ND (N là trung điểm của CD).
Do đó MNC = MND (hai cạnh góc vuông).
c) Vì MNC = MND (chứng minh câu b)
Nên (hai góc tương ứng). (1)
Do AM // DN nên (hai góc so le trong). (2)
Do BM // CN nên (hai góc so le trong). (3)
Từ (1), (2) và (3) suy ra .
Vậy
d)Vì MNC = MND (chứng minh câu b)
Nên MC = MD (hai cạnh tương ứng).
Xét AMD và BMC có:
AM = BM (M là trung điểm của AB),
(chứng minh trên),
MD = MC (chứng minh trên)
Do đó AMD = BMC (c.g.c)
Suy ra AD = BC (hai cạnh tương ứng) và (hai góc tương ứng).
Vậy AD = BC và .
e) Vì AMD = BMC (chứng minh câu d)
Nên (hai góc tương ứng).
Mà (chứng minh câu c)
Do đó
Hay .
Vậy
Bài 3 trang 103 Toán 7 Tập 2: Cho ba điểm A, B, C thẳng hàng, điểm B nằm giữa hai điểm A và C. Gọi a và b lần lượt là đường trung trực của các đoạn thẳng AB và BC. Chứng minh rằng a // b.
Lời giải:
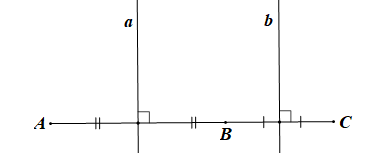
a là đường trung trực của đoạn thẳng AB nên a AB tại trung điểm của AB.
b là đường trung trực của đoạn thẳng BC nên b BC tại trung điểm của BC.
Do A, B, C thẳng hàng và B nằm giữa A và C nên trung điểm của đoạn thẳng AB và trung điểm của đoạn thẳng BC không trùng nhau.
Do đó đường thẳng a và đường thẳng b là hai đường thẳng phân biệt.
Ta có: a AB, b BC, a ≠ b
Do đó a // b.
Vậy a // b.
Bài 4 trang 103 Toán 7 Tập 2: Cho đường thẳng d là đường trung trực của đoạn thẳng AB. Điểm M không thuộc đường thẳng d và đoạn thẳng AB sao cho đường thẳng d cắt đoạn thẳng MB tại điểm I. Chứng minh:
a) MB = AI + IM;
b) MA < MB.
Lời giải:
|
GT |
d là đường trung trực của đoạn thẳng AB, M ∉ d, M ∉ AB, d cắt đoạn thẳng MB tại I |
|
KL |
a) MB = AI + IM; b) MA < MB. |
Chứng minh (Hình vẽ dưới đây):
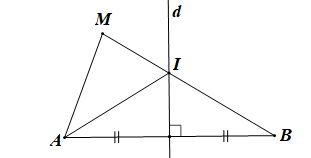
a) Đường thẳng d cắt đoạn thẳng MB tại I nên I thuộc đường trung trực của đoạn thẳng AB.
Do đó AI = BI (tính chất đường trung trực của đoạn thẳng AB)
Khi đó MB = BI + IM = AI + IM.
Vậy MB = AI + IM.
b) Xét trong tam giác AIM có AI + IM > MA (bất đẳng thức trong tam giác)
Mà MB = AI + IM (chứng minh câu a) nên MB > MA.
Vậy MB > MA.
Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:
Bài 10: Tính chất ba đường trung tuyến của tam giác
Bài 11: Tính chất ba đường phân giác của tam giác
Bài 12: Tính chất ba đường trung trực của tam giác
Bài 13: Tính chất ba đường cao của tam giác
Bài tập cuối chương 7
Đăng bởi: THCS Bình Chánh
Chuyên mục: Toán 7 Cánh Diều
- Giải Bài 9.29 trang 81 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 9.30 trang 81 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.33 trang 21 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.27 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.28 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.29 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống









