Toán 7 Kết nối tri thức: Luyện tập chung trang 74

Mời các em theo dõi nội dung bài học do thầy cô trường Trung học Bình Chánh biên soạn sẽ giúp các em nắm chắc kiến thức nội dung bài học tốt hơn.

Giải bài tập Toán 7 Luyện tập chung trang 74 

Giải Toán 7 trang 74 Tập 1

Bạn đang xem: Toán 7 Kết nối tri thức: Luyện tập chung trang 74

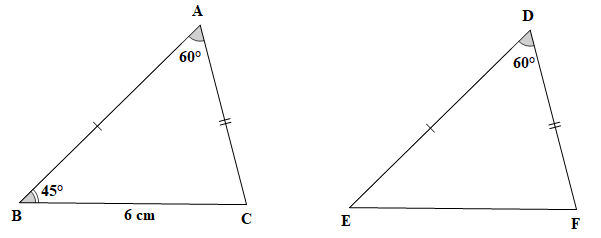
Bài 4.16 trang 74 Toán 7 Tập 1: Cho hai tam giác ABC và DEF thỏa mãn AB = DE, AC = DF, $\widehat{BAC}=\widehat{E\text{D}F}=60°,$BC = 6 cm, $\widehat{ABC}=45°.$ Tính độ dài cạnh EF và số đo các góc ACB, DEF, EFD.

Lời giải:

+) Trong tam giác ABC có $\widehat{BAC}=60°,$ $\widehat{ABC}=45°$, theo định lí tổng ba góc trong một tam giác ta có: $\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180°.$ 

Suy ra $\widehat{ACB}=180°-\widehat{BAC}-\widehat{ABC}$

Hay $\widehat{ACB}=180°-60°-45°=75°.$

+) Xét tam giác ABC và tam giác DEF có:

AB = DE (theo giả thiết);

$\widehat{BAC}=\widehat{E\text{D}F}\left(=60°\right)$ (theo giả thiết);

AC = DF (theo giả thiết).

Vậy $\Delta ABC=\Delta DEF$ (c.g.c).

Suy ra: BC = EF (hai cạnh tương ứng) và $\widehat{ACB}=\widehat{DFE};\widehat{ABC}=\widehat{DEF}$ (các cặp góc tương ứng).

Mà BC = 6 cm; $\widehat{ABC}=45°$ (theo giả thiết) và $\widehat{ACB}=75°$ (chứng minh trên).

Do đó EF = 6 cm; $\widehat{DFE}=75°;\widehat{DEF}=45°.$

Vậy EF = 6 cm; $\widehat{ACB}=75°;$ $\widehat{DEF}=45°$ và $\widehat{DFE}=75°.$ 

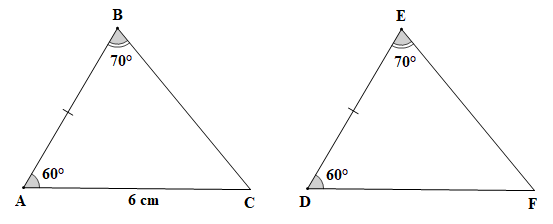
Bài 4.17 trang 74 Toán 7 Tập 1: Cho hai tam giác ABC và DEF thỏa mãn AB = DE, $\widehat{ABC}=\widehat{DEF}=70°,\widehat{BAC}=\widehat{EDF}=60°,$ AC = 6 cm. Tính độ dài cạnh DF.

Lời giải:

Xét tam giác ABC và tam giác DEF có:

$\widehat{BAC}=\widehat{E\text{D}F}\left(=60°\right)$(theo giả thiết);

AB = DE (theo giả thiết);

$\widehat{ABC}=\widehat{DEF}\left(=70°\right)$(theo giả thiết).

Vậy $\Delta ABC=\Delta DEF$ (g.c.g).

Suy ra: AC = DF (hai cạnh tương ứng).

Mà AC = 6 cm (theo giả thiết).

Do đó DF = 6 cm. 

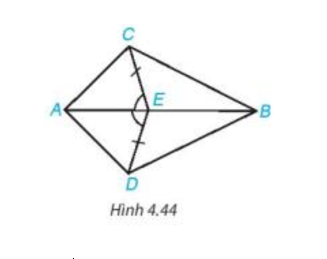
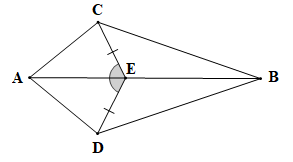
Bài 4.18 trang 74 Toán 7 Tập 1: Cho Hình 4.44, biết EC = ED và $\widehat{A\text{E}C}=\widehat{A\text{ED}}.$ Chứng minh rằng:

a) $\Delta A\text{E}C=\Delta A\text{ED};$

b) $\Delta ABC=\Delta AB\text{D}.$

Lời giải:

a) Xét tam giác AEC và tam giác AED có:

EC = ED (theo giả thiết);

$\widehat{A\text{E}C}=\widehat{A\text{ED}}$ (theo giả thiết);

AE là cạnh chung.

Vậy $\Delta A\text{E}C=\Delta A\text{ED}$ (c.g.c).

b) Từ $\Delta A\text{E}C=\Delta A\text{ED}$ (chứng minh ở câu a)

Suy ra AC = AD (hai cạnh tương ứng);

Và $\widehat{CAE}=\widehat{DAE}$ (hai góc tương ứng) hay $\widehat{CAB}=\widehat{DAB}$.

Xét tam giác ABC và tam giác ABD có:

AC = AD (theo giả thiết);

$\widehat{CAB}=\widehat{DAB}$ (theo giả thiết);

AB là cạnh chung.

Vậy $\Delta ABC=\Delta AB\text{D}$ (c.g.c). 

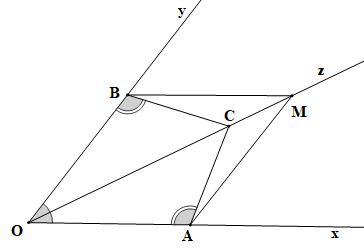
Bài 4.19 trang 74 Toán 7 Tập 1: Cho tia Oz là tia phân giác của góc xOy. Lấy các điểm A, B, C lần lượt thuộc các tia Ox, Oy, Oz sao cho $\widehat{CAO}=\widehat{CBO}.$

a) Chứng minh rằng $\Delta OAC=\Delta OBC.$

b) Lấy điểm M trên tia đối của tia CO. Chứng minh rằng $\Delta MAC=\Delta MBC.$

Lời giải:

a)

+) Tia Oz là tia phân giác của góc xOy (theo giả thiết) nên $\widehat{xOz}=\widehat{yOz}$ (tính chất tia phân giác của một góc).

 Suy ra $\widehat{AOC}=\widehat{BOC}$.

+) Áp dụng định lí tổng ba góc trong một tam giác cho tam giác OAC và OBC ta có:

Trong tam giác OAC: $\widehat{AOC}+\widehat{OCA}+\widehat{CAO}=180°$ suy ra $\widehat{OCA}=180°-\left(\widehat{AOC}+\widehat{CAO}\right);$

Trong tam giác OBC: $\widehat{BOC}+\widehat{OCB}+\widehat{CBO}=180°$ suy ra $\widehat{OCB}=180°-\left(\widehat{BOC}+\widehat{CBO}\right);$

Mà $\widehat{AOC}=\widehat{BOC}$ (chứng minh trên) và $\widehat{CAO}=\widehat{CBO}$ (theo giả thiết).

Do đó $\widehat{AOC}+\widehat{CAO}$ = $\widehat{BOC}+\widehat{CBO}$.

Suy ra $180°-\left(\widehat{AOC}+\widehat{CAO}\right)=180°-\left(\widehat{BOC}+\widehat{CBO}\right).$

Hay $\widehat{OCA}=\widehat{OCB}$.

+) Xét tam giác OAC và tam giác OBC có:

$\widehat{AOC}=\widehat{BOC}$ (chứng minh trên);

OC là cạnh chung;

$\widehat{OCA}=\widehat{OCB}$ (chứng minh trên).

Vậy $\Delta OAC=\Delta OBC$ (g.c.g).

b) Từ $\Delta OAC=\Delta OBC$ (chứng minh câu a) suy ra OA = OB (hai cạnh tương ứng).

Xét tam giác OAM và tam giác OBM có:

OA = OB (chứng minh trên);

$\widehat{AOM}=\widehat{BOM}$ (do $\widehat{xOz}=\widehat{yOz}$);

OM là cạnh chung.

Vậy $\Delta OAM=\Delta OBM$ (c – g – c)

Do đó, $\widehat{BMO}=\widehat{AMO}$  (hai góc tương ứng) hay $\widehat{BMC}=\widehat{AMC}$

BM = MA (hai cạnh tương ứng)

Xét tam giác MAC và MBC có:

$\widehat{BMC}=\widehat{AMC}$ (chứng minh trên)

BM = MA

CM chung

Vậy $\Delta MAC=\Delta MBC$ (c.g.c). 

Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 15: Các trường hợp bằng nhau của tam giác vuông

Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng

Luyện tập chung trang 85, trang 86

Bài tập cuối chương 4 trang 87

Bài 17: Thu thập và phân loại dữ liệu

Đăng bởi: THCS Bình Chánh

Chuyên mục: Giải Toán 7 Kết nối tri thức

• Giải Bài 9.29 trang 81 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
• Giải Bài 9.30 trang 81 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
• Giải Bài 6.33 trang 21 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
• Giải Bài 6.27 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
• Giải Bài 6.28 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
• Giải Bài 6.29 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống