Giải Bài 9.23 trang 76 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
Mời các em theo dõi nội dung bài học do thầy cô trường THCS Bình Chánh biên soạn sẽ giúp các em nắm chắc kiến thức nội dung bài học tốt hơn.
Bài 9.23 trang 76 SGK Toán 7 tập 2
Toán 7 tập 2 Bài 9.23 trang 76 là lời giải bài Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác SGK Toán 7 sách Kết nối tri thức với cuộc sống hướng dẫn chi tiết lời giải giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 7. Mời các em học sinh cùng tham khảo chi tiết.
Giải bài 9.23 Toán 7 trang 76
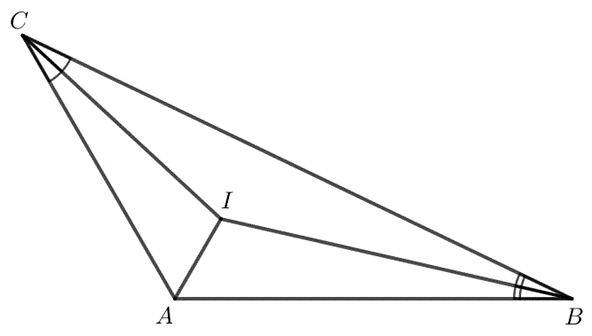
| Bài 9.23 (SGK trang 76): Kí hiệu I là điểm đồng quy của ba đường phân giác trong tam giác ABC. Tính góc BIC biết góc BAC bằng 120o. |
Hướng dẫn giải
Bạn đang xem: Giải Bài 9.23 trang 76 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
+ Ba đường trung tuyến của một tam giác cùng đi qua một điểm (hay đồng quy tại một điểm). Điểm đó cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.
+ Ba đường phân giác của một tam giác đồng quy tại một điểm. Điểm này cách đều ba cạnh của tam giác đó.
Lời giải chi tiết
Hình vẽ minh họa:
Xét tam giác ABC có:
Ta có:
CI là tia phân giác của
=>
BI là tia phân giác của
=>
Xét tam giác IBC có:
Câu hỏi cùng bài:
- Bài 9.24 trang 76 SGK Toán 7 tập 2
- Bài 9.25 (SGK trang 76): Trong tam giác ABC, hai đường phân giác của các góc B và C cắt nhau tại D.
- Bài 9.26 (SGK trang 81): Gọi H là trực tâm của tam giác ABC không vuông …
- Bài 9.27 (SGK trang 81): Cho tam giác ABC có
và trực tâm H. Tính góc BHC.
- Bài 9.28 (SGK trang 81): Xét điểm O cách đều ba đỉnh của tam giác ABC …
- Bài 9.29 (SGK trang 81): a) Có một chi tiết máy (đường viền ngoài là đường tròn) ….
- Bài 9.30 (SGK trang 81): Cho hai đường thẳng không vuông góc b, c cắt nhau tại điểm A …
Bài tiếp theo: Bài 35 Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác
—————————————-
Trên đây là lời giải chi tiết Bài 9.23 Toán 7 trang 76 Sự đồng quy của ba trung tuyến, ba đường phân giác trong một tam giác cho các em học sinh tham khảo, nắm được cách giải các dạng toán của Chương 9: Quan hệ giữa các yếu tố trong một tam giác. Qua đó giúp các em học sinh ôn tập chuẩn bị cho các bài thi giữa và cuối học kì lớp 7. Chúc các em học tốt. Mời thầy cô và học sinh tham khảo thêm tài liệu: Giải Toán 7 tập 2 KNTT, Giải Toán 7 Chân trời sáng tạo tập 2, Giải Toán 7 Tập 2 sách Cánh Diều
Đăng bởi: THCS Bình Chánh
Chuyên mục: Toán 7 Kết nối tri thức
- Giải Bài 9.29 trang 81 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 9.30 trang 81 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.33 trang 21 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.27 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.28 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.29 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống