Công thức hạ bậc và bài tập vận dụng

Cô Nguyễn Thanh Phương 28/05/2023

Mời các em theo dõi nội dung bài học về Công thức hạ bậc và bài tập vận dụng do thầy cô trường THCS Bình Chánh biên soạn. Hy vọng sẽ là tài liệu hữu ích giúp các em học tốt và hoàn thành tốt bài tập của mình.

Mục lục

Lượng giác là gì?

Lượng giác tên tiếng Anh là Trigonometry là một nhánh nhỏ trong toán học, sử dụng để tìm hiểu về hình tam giác và sự liên kết giữa cạnh của hình tam giác với góc độ của nó. Lượng giác giúp chỉ ra hàm số lượng giác, mà hàm số lượng giác diễn tả những mối liên kết và có thể áp dụng được để học các hiện tượng có chu kỳ như song âm.

Hạ bậc lượng giác là gì?

Hạ bậc lượng giác là tìm cách để đưa những hàm số lượng giác có bậc cao về bậc thấp hơn nó.

Bạn đang xem: Công thức hạ bậc và bài tập vận dụng

Công thức hạ bậc

Công thức hạ bậc bậc hai

$\cos a = \pm \sqrt {\frac{{1 + \cos 2a}}{2}}$

$\sin a = \pm \sqrt {\frac{{1 - \cos 2a}}{2}}$

$\tan a = \pm \sqrt {\frac{{1 - \cos 2a}}{{1 + \cos 2a}}}$

Công thức hạ bậc bậc 3

$\sin a = \sqrt[3]{{\frac{{3\sin a - \sin 3a}}{4}}}$

$\tan a = \sqrt[3]{{\frac{{3\sin a - \sin 3a}}{{3\cos a + \cos 3a}}}}$

Công thức hạ bậc bậc bốn

$\sin a = \pm \sqrt[4]{{\frac{{\cos 4a - 4\cos s2a + \dfrac{6}{2}}}{8}}}$

$\cos a = \pm \sqrt[4]{{\frac{{\cos 4a + 4\cos s2a + \dfrac{6}{2}}}{8}}}$

Công thức hạ bậc bậc 5

$\sin a = \sqrt[5]{{\frac{{\sin 5a - 5\sin 3a + 10\sin a}}{{16}}}}$

$\cos a = \sqrt[5]{{\frac{{\cos 5a + 5\cos 3a + 10\cos a}}{{16}}}}$

Ví dụ minh họa

Ví dụ : Giải phương trình lượng giác: sin 2 x = cos 2 x + cos 2 3x

Lời giải

Biến đổi phương trình về dạng:

$\frac{{1 - \cos 2x}}{2} = \frac{{1 + \cos 4x}}{2} + {\cos ^2}3x$

<=> 2cos23x + (cos4x + cos2x) = 0

<=> 2cos23x + 2cos3x . cosx = 0

<=> (cos3x + cosx) . cos3x = 0

<=> 2cos2x . cosx . cos3x = 0

$\Leftrightarrow \left[ {\begin{array}{*{20}{c}} {\cos 2x = 0} \\ {\cos x = 0} \\ {\cos 3x = 0} \end{array}} \right. \Rightarrow \left[ {\begin{array}{*{20}{c}} {2x = \dfrac{\pi }{2} + k\pi } \\ {x = \dfrac{\pi }{2} + k\pi } \\ {3x = \dfrac{\pi }{2} + k\pi } \end{array}} \right. \Rightarrow \left[ {\begin{array}{*{20}{c}} {x = \dfrac{\pi }{4} + \dfrac{{k\pi }}{2}} \\ {x = \dfrac{\pi }{2} + k\pi } \\ {x = \dfrac{\pi }{6} + \dfrac{{k\pi }}{3}} \end{array}} \right.\left( {k \in \mathbb{Z}} \right)$

Cách học công thức hạ bậc lượng giác bằng thơ

Một số đoạn thơ vui mà bạn có thể học để ghi nhớ các công thức hạ bậc lượng giác:

Sao đi học (sin = đối/ huyền)

Cứ khóc hoài (cos = kề/ huyền)

Thôi đừng khóc (tan = đối/ kề)

Có kẹo đây (cot = kề/ đối)

Tìm sin lấy đối chia huyền

Cosin thì lấy cạnh kề, huyền chia nhau.

Còn tang ta tính như sau:

Đối trên, kề dưới chia nhau là ra liền.

Cotang cũng rất dễ ăn tiền,

Kề trên, đối dưới chia liền thể nào cũng ra

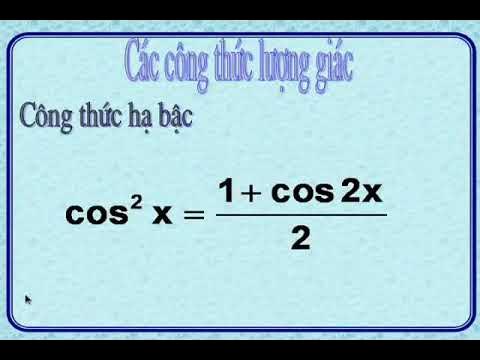
Bài tập vận dụng về hạ bậc lượng giác

Bài tập 1. Giải phương trình lượng giác sau: sin3a + cos3a = 0

Lời giải

(1 – cos3a)/2 + cos3a = 0

⇔1 – cos3a + 2cos3a = 0

⇔1 + cos3a = 0

⇔ cos3a = -1

⇔3a = π + k2π

Vậy nghiệm của phương trình lượng giác này là 3a = π + k2π

Bài tập 2: Hãy giải phương trình sin2x = cos2x + cos25x

Lời giải

Biến đổi phương trình về dạng:

(1 – cos2x)/2 = (1 + cos4x)/2 + cos25x

⇔ 2cos25x + (cos4x + cos2x) = 0

⇔ 2cos25x + 2cos3x.cos5x = 0

⇔ (cos3x + cosx) cos5x = 0

⇔ 2cos2x.cosx.cos5x = 0

Bài tập 3: giải phương trình lượng giác sau:

$\begin{aligned} &\sin 2 a+\cos 2 a=0 \\ &\Leftrightarrow=>(1-\cos 2 a) / 2+\cos 2 a=0 \\ &\Leftrightarrow 1-\cos 2 a+2 \cos 2 a=0 \\ &\Leftrightarrow 1+\cos 2 a=0 \\ &\Leftrightarrow \cos 2 a=-1 \\ &\Leftrightarrow 2 a=\pi+k 2 \pi \\ &\Leftrightarrow a=\pi / 2+k \pi \end{aligned}$

Vậy nghiệm của phương trình lượng giác là $\mathrm{a}=\pi / 2+\mathrm{k} \pi$

Bài tập 4:

Rút gọn biểu thức $\displaystyle A = {{{\mathop{\rm s}\nolimits} {\rm{inx}} + \sin 3{\rm{x}} + \sin 5{\rm{x}}} \over {{\mathop{\rm cosx}\nolimits} + \cos 3x + \cos5x}}.$

Áp dụng các công thức:

$\begin{array}{l} + )\;\;\sin a + \sin b = 2\sin \dfrac{{a + b}}{2}\cos \dfrac{{a - b}}{2}.\\ + )\;\;\cos a + \cos b = 2\cos \dfrac{{a + b}}{2}\cos \dfrac{{a - b}}{2}.\\ + )\;\;\tan a = \dfrac{{\sin a}}{{\cos a}}. \end{array}$

Trả lời

Ta có:

$\sin x + \sin 3x + \sin 5x$

$= (\sin 5x + \sin x) + \sin 3x$

$= 2\sin {{5x + x} \over 2}.\cos {{5x - x} \over 2} + \sin 3x$

$= 2\sin 3x \cos 2x + \sin 3x$

$= \sin 3x (2\cos 2x + 1) \, \, \, \, (1)$

$\cos x + \cos3x + \cos5x$

$= (\cos 5x + \cos x )+\cos3x$

$= 2\cos \dfrac{{5x + x}}{2}\cos \dfrac{{5x - x}}{2}+ \cos3x$

$= 2\cos3x . \cos2x + \cos3x$

$= \cos3x (2\cos2x + 1) \, \, \, (2)$

Từ (1) và (2) ta có:

$A = \dfrac{{\sin 3x\left( {2\cos 2x + 1} \right)}}{{\cos 3x\left( {2\cos 2x + 1} \right)}} = {{\sin 3x} \over {\cos 3x}} = \tan 3x$

Vậy $A= \tan 3x.$

***

Trên đây là nội dung bài học Công thức hạ bậc và bài tập vận dụng do thầy cô trường THCS Bình Chánh biên soạn và tổng hợp. Hy vọng sẽ giúp các em hiểu rõ nội dung bài học và từ đó hoàn thành tốt bài tập của mình. Đồng thời luôn đạt điểm cao trong các bài thi bài kiểm tra sắp tới. Chúc các em học tập thật tốt.

Đăng bởi THCS Bình Chánh trong chuyên mục Học tập