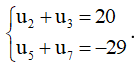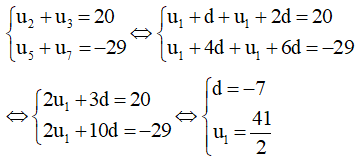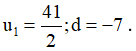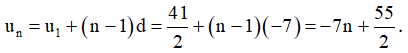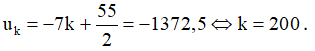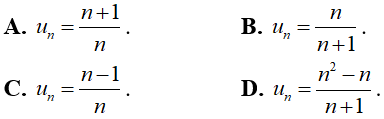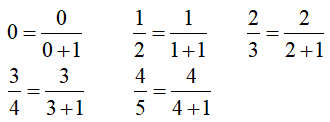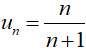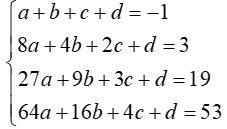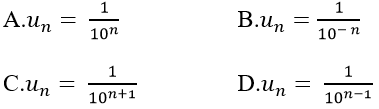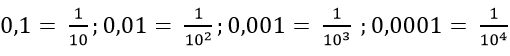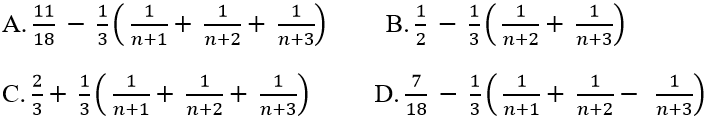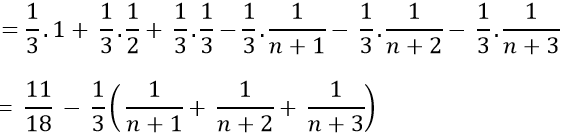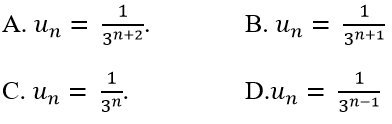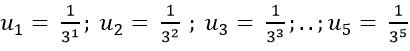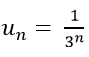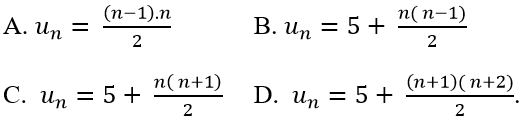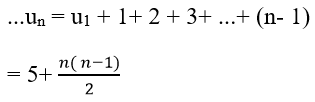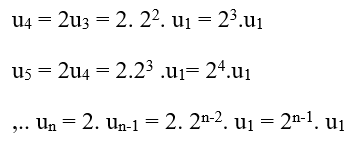Công thức số hạng tổng quát và ví dụ minh họa

Cô Nguyễn Thanh Phương 23/05/2023

Mời các em theo dõi nội dung bài học về Công thức số hạng tổng quát và ví dụ minh họa do thầy cô trường THCS Bình Chánh biên soạn. Hy vọng sẽ là tài liệu hữu ích giúp các em học tốt và hoàn thành tốt bài tập của mình.

Mục lục

Công thức số hạng tổng quát

Lý thuyết

a) (u_n) là cấp số cộng khi u_n+1 = u_n + d, n ∈ N^* (d gọi là công sai)

Bạn đang xem: Công thức số hạng tổng quát và ví dụ minh họa

b) Số hạng tổng quát của cấp số cộng (u_n) được xác định bởi công thức:

u_n = u₁ + (n – 1)d với n ∈ N^*.

Công thức

Số hạng tổng quát của cấp số cộng (u_n) được xác định bởi công thức:

u_n = u₁ + (n – 1)d với n ∈ N^*.

Ví dụ minh họa

Ví dụ 1: Cho cấp số cộng (u_n) có u₁ = 1 và d = – 3.

a) Xác định số hạng tổng quát của cấp số cộng

b) Tìm số hạng thứ 2021 của cấp số cộng

c) Số – 488 là số hạng thứ bao nhiêu của cấp số cộng.

Lời giải

a) Số hạng tổng quát:

u_n = u₁ + (n – 1)d = 1 + (n – 1).(– 3) = – 3n + 4.

b) Số hạng thứ 2021 của cấp số cộng:

u₂₀₂₁ = – 3.2021 + 4 = – 6059.

c) Gọi số hạng thứ k là số – 488, ta có: u_k = – 3k + 4 = – 488. Suy ra k = 164.

Vậy số – 488 là số hạng thứ 164.

Ví dụ 2: Cho cấp số cộng (u_n) thỏa mãn

a) Tìm u₁; d?

b) Xác định số hạng tổng quát của cấp số cộng.

c) Số –1372,5 là số hạng thứ bao nhiêu của cấp số cộng.

Lời giải

a) Ta có:

Vậy

b) Số hạng tổng quát:

c) Gọi số hạng thứ k là số – 1372,5, ta có:

Vậy số – 1372,5 là số hạng thứ 200.

Ví dụ 3: Cho dãy số có các số hạng đầu là: 4; 8; 12; 16; 20; 24;… Số hạng tổng quát của dãy số này là:

A. u_n = 4n

B. u_n = 2n+ 2

C. u_n = 2n+ 5

D. u_n = 4n+ 2

Lời giải

Ta có:

4 = 4.1 8 = 4.2 12 = 4.3

16 = 4.4 20 = 4.5 24 = 4.6

Suy ra số hạng tổng quát u_n = 4n.

Chọn A .

Ví dụ 4: Cho dãy số có các số hạng đầu là: .Số hạng tổng quát của dãy số này là:

A. u_n = 7n + 7.

B. u_n = 7n .

C. u_n = 7n + 1.

D. u_n : Không viết được dưới dạng công thức.

Lời giải

Ta có:

8 = 7 . 1 + 1 15 = 7 . 2 + 1 22 = 7 . 3 + 1

29 = 7 . 4 + 1 36 = 7 . 5 + 1

Suy ra số hạng tổng quát u_n = 7n + 1.

Chọn C.

Ví dụ 5: Cho dãy số có các số hạng đầu là:

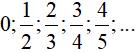.Số hạng tổng quát của dãy số này là:

Lời giải

Ta có:

Suy ra số hạng tổng quát của dãy số là:

Chọn B.

Ví dụ 6: Cho dãy số có 4 số hạng đầu là: − 1, 3, 19, 53. Hãy tìm một quy luật của dãy số trên và viết số hạng thứ 10 của dãy với quy luật vừa tìm.

A. u₁₀ = 971

B. u₁₀ = 837

C. u₁₀ = 121

D. u₁₀ = 760

Lời giải

Xét dãy (u_n) có dạng: u_n = an³ + bn² + cn + d

Theo giả thiết ta có: u₁ = − 1; u₂ = 3; u₃ = 19 và u₄ = 53

=> hệ phương trình:

Giải hệ trên ta tìm được: a = 1;b = 0 ; c = −3 và d = 1.

Khi đó; số hạng tổng quát của dãy số là: u_n = n³ − 3n+ 1

Số hạng thứ 10: u₁₀ = 971 .

Chọn A .

Ví dụ 7: Cho dãy số có các số hạng đầu là:0,1; 0,01; 0,001; 0,0001…. Số hạng tổng quát của dãy số này có dạng?

Lời giải

Ta thấy:

=> Số hạng thứ n là:

Chọn A.

Ví dụ 8: Cho 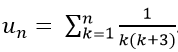. Xác định công thức tính u_n

Lời giải

Ta có:

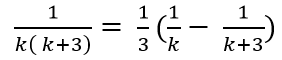
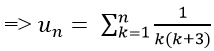
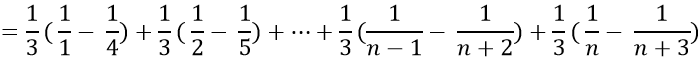
Chọn C.

Ví dụ 9: Cho dãy số có các số hạng đầu là: − 2; 0; 2; 4; 6…Số hạng tổng quát của dãy số này có dạng?

A. u_n = −2n .

B. u_n = − 2 + n .

C. u_n = − 2(n+ 1) .

D.u_n = − 2 + 2(n − 1)

Lời giải

Dãy số là dãy số cách đều có khoảng cách là 2 và số hạng đầu tiên là (−2) nên

u_n = − 2 + 2(n − 1) .

chọn D.

Ví dụ 10: Cho dãy số có các số hạng đầu là: 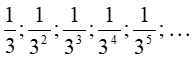.Số hạng tổng quát của dãy số này là?

Hướng dẫn giải:

Ta có;

=> Số hạng thứ n của dãy số là:

Chọn C.

Ví dụ 11: Cho dãy số (u_n) với 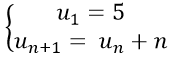.Số hạng tổng quát u_n của dãy số là số hạng nào dưới đây?

Lời giải

Ta có:

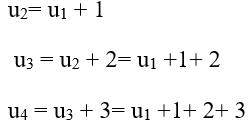
Chọn B.

Ví dụ 12: Cho dãy số (u_n) với 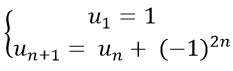. Số hạng tổng quát u_n của dãy số là số hạng nào dưới đây?

A. u_n = 1 + n

B. u_n = n(n + 1)

C. u_n = 1 + (−1)²ⁿ.

D. u_n = n

Lời giải

* Ta có: u_n+1 = u_n + (−1)²ⁿ = u_n + 1 (vì (−1)²ⁿ = ((−1)²)ⁿ = 1

=> u₂ = 2 ; u₃ = 3; u₄ = 4; …

Dễ dàng dự đoán được: u_n= n.

Thật vậy, ta chứng minh được : u_n = n bằng phương pháp quy nạp như sau:

+ Với n = 1 => u₁ = 1. Vậy (*) đúng với n = 1.

+ Giả sử (*) đúng với mọi n = k ( k ∈ N*), ta có u_k = k.

Ta đi chứng minh (*) cũng đúng với n = k + 1, tức là u_k+1 = k + 1

+ Thật vậy, từ hệ thức xác định dãy số (un ) ta có: u_k+1 = u_k + 1= k+ 1

Vậy (*) đúng với mọi n.

Chọn D.

Ví dụ 13: Cho dãy số (u_n) với 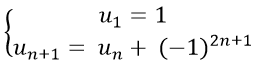. Số hạng tổng quát un của dãy số là số hạng nào dưới đây?

A. u_n = 2 − n

B. không xác định.

C. u_n = 1 − n.

D. u_n = −n với mọi n.

Lời giải

+ Ta có: u₂ = 0; u₃ = −1; u₄ = −2…

Dễ dàng dự đoán được u_n = 2 − n.

+ Thật vậy; với n = 1 ta có: u₁ = 1 ( đúng)

Giả sử với mọi n = k ( k ∈ N*) thì u_k = 2 − k.

Ta chứng minh: u_k+1 = 2 − (k+ 1)

Theo giả thiết ta có: u_{k + 1} = u_k + (−1)^{2k + 1} = 2 − k − 1 = 2 − (k+1)

=> điều phải chứng minh.

Ví dụ 14: Cho dãy số (u_n) với 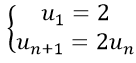.Công thức số hạng tổng quát của dãy số này :

A. u_n = nⁿ⁻¹.

B. u_n = 2ⁿ.

C. u_n = 2ⁿ⁺¹.

D. u_n = 2^{n − 1}

Hướng dẫn giải:

+ Ta có:

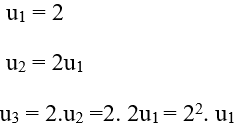
Hay u_n = 2ⁿ (vì u₁ = 2)

Chọn B.

Trên đây là nội dung bài học Công thức số hạng tổng quát và ví dụ minh họa do thầy cô trường THCS Bình Chánh biên soạn và tổng hợp. Hy vọng sẽ giúp các em hiểu rõ nội dung bài học và từ đó hoàn thành tốt bài tập của mình. Đồng thời luôn đạt điểm cao trong các bài thi bài kiểm tra sắp tới. Chúc các em học tập thật tốt.

Đăng bởi THCS Bình Chánh trong chuyên mục Học tập