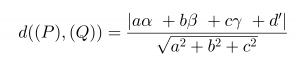Mời các em theo dõi nội dung bài học về Công thức tính khoảng cách giữa 2 mặt phẳng? Ví dụ cụ thể do thầy cô trường THCS Bình Chánh biên soạn. Hy vọng sẽ là tài liệu hữu ích giúp các em học tốt và hoàn thành tốt bài tập của mình.
Khái niệm công thức tính khoảng cách
Trước hết, chúng ta cần biết rằng trong không gian hai mặt phẳng có 3 vị trí tương đối. Đó là hai mặt phẳng trùng nhau, hai mặt phẳng song song và hai mặt phẳng cắt nhau. Trong hai trường hợp mặt phẳng cắt nhau và trùng nhau ta có thể coi khoảng cách giữa chúng bằng 0. Người ta cũng không hỏi khoảng cách giữa hai mặt phẳng trong trường hợp này. Vì vậy chúng ta chỉ xét khoảng cách giữa hai mặt phẳng song song mà thôi.
Định nghĩa:
Bạn đang xem: Công thức tính khoảng cách giữa 2 mặt phẳng? Ví dụ cụ thể
Trước hết, ta nhắc lại định nghĩa khoảng cách từ một điểm M lên mặt phẳng (P) là khoảng cách giữa M và hình chiếu của nó trên mặt phẳng (P). Ký hiệu là d(M,(P)).
Cho hai mặt phẳng (P) và (Q) song song với nhau. Khoảng cách giữa mặt phẳng (P) và (Q) là khoảng cách từ một điểm M bất kỳ trên mặt phẳng (P) đến mặt phẳng (Q) hoặc ngược lại. Ký hiệu là d((P),(Q)).
Các công thức tính khoảng cách
Sau đây là tổng hợp những công thức tính khoảng cách được sử dụng nhiều nhất. Bạn còn chờ đợi gì mà không lưu lại ngay để việc tính toán trở nên đơn giản và dễ dàng hơn bao giờ hết.
Công thức tính khoảng cách giữa 2 mặt phẳng song song
Lý thuyết
Trong không gian Oxyz, cho nhị mặt phẳng song song với nhau với phương trình lần lượt là (α): ax + by + cz + d1 = 0 và (β): ax + by + cz + d2 = 0. Khoảng cách giữa nhì mặt phẳng này được xác định theo công thức
d((α); (β)) = |d1–d2|a2+b2+c2√ với d1 ≠ d2.
Chú ý: Nếu d1 = d2. =≫ nhì mặt phẳng trùng nhau => d((α); (β)) = 0
Công thức tính khoảng cách giữa 2 mặt phẳng trong không gian
Công thức tính khoảng cách giữa 2 mặt phẳng trong không gian là thắc bận bịu được rất nhiều người niềm nở. Đây là một câu hỏi vô cùng cần thiết để giúp Cả nhà có thêm tri thức song song thuận lợi trả lời bài tập của mình. Ngay hiện nay mình hãy cùng nhau theo dõi và giải một số bài toán nhé!
Ngay bây giờ hãy cùng chúng tôi đi mày mò công thức tính khoảng cách giữa 2 mặt phẳng trong không gian. Qua đó Anh chị sẽ dễ ợt giải được những bài tập tương tác tới tính khoảng cách giữa 2 mặt phẳng trong không gian
Cho nhì mặt phẳng (P), (Q) song song trong không gian. Phương trình của chúng đều có thể đưa về dạng:
(P): ax+by+cz+d=0 và (Q): ax+by+cz+d’=0 (a²+b²+c²>0 và d≠d’)
Khi đó giả sử M(α;β;γ) thuộc mặt phẳng (P) ta có: aα+bβ+cγ=-d. Khoảng cách giữa (P) và (Q)chính là khoảng cách giữa M và (Q). bởi đó:
Công thức Khoảng cách giữa 2 mặt phẳng trong không gian:
Trường hợp nào khoảng cách giữa hai mặt phẳng bằng 0?
Khoảng cách giữa hai mặt phẳng bằng 0 khi hai mặt phẳng cắt nhau hoặc trùng nhau. Điều này có nghĩa là hai mặt phẳng gần như giống nhau hoặc hoàn toàn trùng lên nhau. Khi đó, để tính khoảng cách giữa hai mặt phẳng, ta có thể coi giá trị khoảng cách bằng 0.
Tính khoảng cách giữa hai mặt phẳng song song chứa hai đường thẳng đã cho như thế nào?
Giả sử hai đường thẳng đã cho có phương trình lần lượt là:
d1: (x, y, z) = (x1, y1, z1) + t(a1, b1, c1)
d2: (x, y, z) = (x2, y2, z2) + s(a2, b2, c2)
Trong đó, t và s là các tham số thực bất kỳ.
Ta dùng phương pháp sau để tính khoảng cách giữa hai mặt phẳng song song chứa hai đường thẳng đã cho:
- Bước 1: Tìm vector pháp tuyến của mặt phẳng chứa đường thẳng d1 bằng cách lấy tích vô hướng của hai vector (a1, b1, c1) và (x0, y0, z0) với điểm (x0, y0, z0) là một điểm trên đường thẳng d1. Ta có:
n = (a1, b1, c1) . (x0, y0, z0) - Bước 2: Tìm mặt phẳng chứa đường thẳng d1 bằng cách sử dụng phương trình mặt phẳng chung của hai vector (x0, y0, z0) và (a1, b1, c1) với điểm M(x, y, z) trên mặt phẳng như sau:
a1(x – x0) + b1(y – y0) + c1(z – z0) = 0 - Bước 3: Viết lại phương trình trên dưới dạng: a1x + b1y + c1z + d1 = 0 với d1 = -a1x0 – b1y0 – c1z0
- Bước 4: Áp dụng phương trình mặt phẳng chứa đường thẳng d2 để tìm khoảng cách giữa hai mặt phẳng. Ta thay vào phương trình của mặt phẳng chứa đường thẳng d2 thì ta sẽ có:
a1x2 + b1y2 + c1z2 + d1 = 0
a1(x2 + sa2) + b1(y2 + sb2) + c1(z2 + sc2) + d1 = 0
Vì hai mặt phẳng song song nên khoảng cách giữa chúng bằng khoảng cách giữa một điểm trên mặt phẳng thứ nhất với mặt phẳng thứ hai. Vì vậy, ta có:
Khoảng cách giữa hai mặt phẳng = |(a1x2 + b1y2 + c1z2 + d1) / sqrt(a1^2 + b1^2 + c1^2)|
Làm thế nào để dựng một mặt phẳng chứa hai đường thẳng để tính khoảng cách giữa hai mặt phẳng chứa hai đường thẳng đó?
- Bước 1: Cho hai đường thẳng đã cho và tìm véc tơ pháp tuyến chung của hai đường thẳng.
- Bước 2: Dựng một điểm trên một trong hai đường thẳng, sau đó kẻ một đường thẳng vuông góc với hai đường thẳng đã cho và đi qua điểm vừa chọn.
- Bước 3: Kẻ một đường thẳng khác vuông góc với hai đường thẳng đã cho và đi qua điểm vừa tìm ở Bước 2.
- Bước 4: Giao điểm của hai đường thẳng vừa kẻ được chọn làm điểm thuộc mặt phẳng cần tìm.
- Bước 5: Viết phương trình của mặt phẳng bằng véc tơ pháp tuyến và điểm thuộc mặt phẳng đã tìm ở Bước 4.
- Bước 6: Tính khoảng cách giữa mặt phẳng mới tìm và mặt phẳng chứa đường thẳng còn lại bằng cách sử dụng công thức tính khoảng cách giữa hai mặt phẳng.
Bài tập có lời giải chi tiết
Bài tập 1. Trong không gian Oxyz, có hai mặt phẳng có phương trình lần lượt là (α): x – 2y + z + 1 = 0 và (β): x – 2y + z + 3 = 0. Hãy tính khoảng cách giữa 2 mặt phẳng?
Hướng dẫn giải
Ta thấy hai mặt phẳng này song song với nhau nên khoảng cách giữa 2 mặt phẳng được xác định theo công thức
d((α); (β)) = |1–3|12+(–2)2√+12=6√3
Kết luận: d((α); (β)) = 6√3
Bài tập 2. Hai mặt phẳng (α) // (β), cách nhau 3. Biết phương trình của mỗi mặt phẳng là (α): 2x – 5y – 3z + 1 = 0 và (β): ax + by + cz + d2 = 0. Hãy xác định các hệ số của phương trình mặt phẳng (β).
Hướng dẫn giải
Vì (α) // (β) => a = 2; b = – 5 và c = – 3
Mặt khác: d((α); (β)) = 3 => |1–d1|22+(–5)2+(–3)2√=3⇔d1=338−−√–1
Kết luận: Phương trình mặt phẳng (β): 2x – 5y – 3z + (338−−√–1) = 0
Trên đây là nội dung bài học Công thức tính khoảng cách giữa 2 mặt phẳng? Ví dụ cụ thể do thầy cô trường THCS Bình Chánh biên soạn và tổng hợp. Hy vọng sẽ giúp các em hiểu rõ nội dung bài học và từ đó hoàn thành tốt bài tập của mình. Đồng thời luôn đạt điểm cao trong các bài thi bài kiểm tra sắp tới. Chúc các em học tập thật tốt.
Đăng bởi THCS Bình Chánh trong chuyện mục Học tập
- Tụ điện là gì? Cấu tạo của tụ điện? Công dụng của tụ điện là gì?
- Gốc axit là gì? Gốc axit được phân thành mấy loại?
- Soạn bài Trái tim Đan-Kô SGK Ngữ văn 11 Cánh diều –
- Soạn bài Một người Hà Nội SGK Ngữ văn 11 Cánh diều –
- Soạn bài Thực hành đọc hiểu Tầng hai SGK Ngữ văn 11 Cánh diều –
- Soạn bài Tác gia Nguyễn Du SGK Ngữ văn 11 Kết nối tri thức