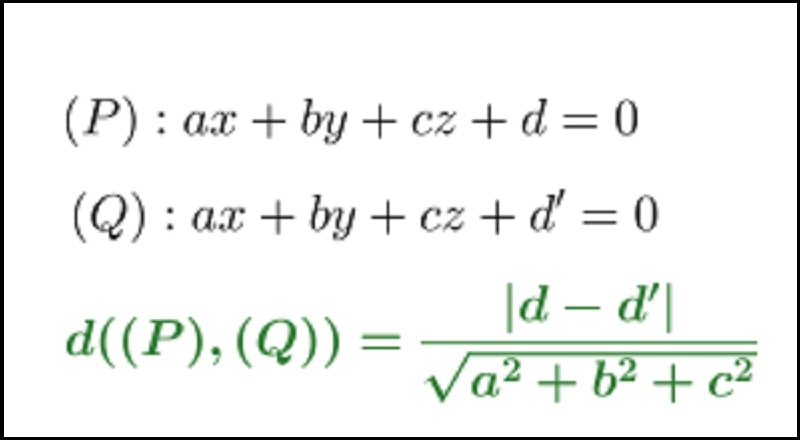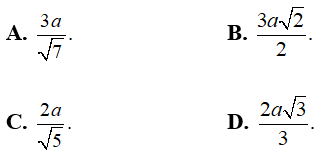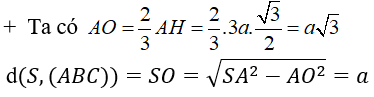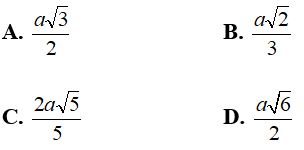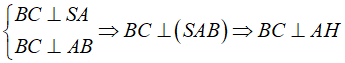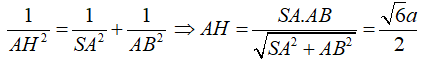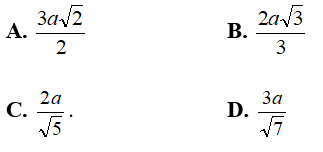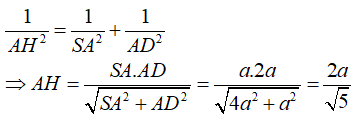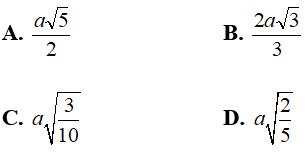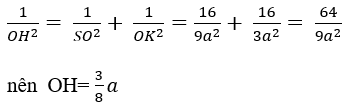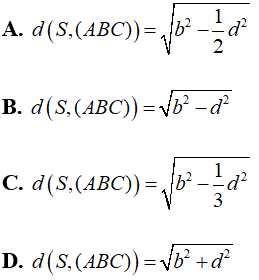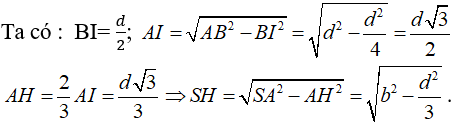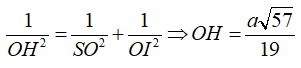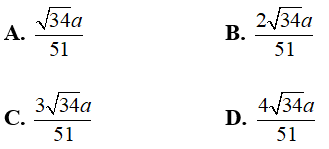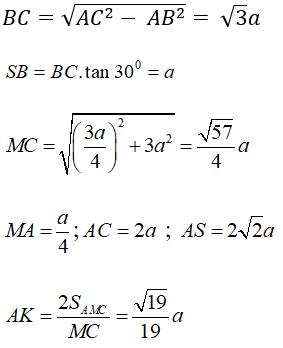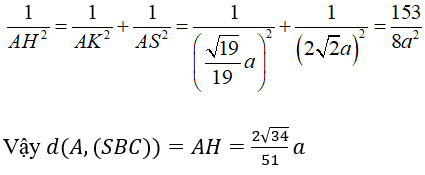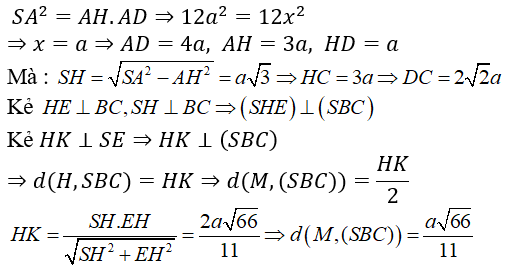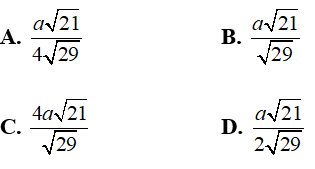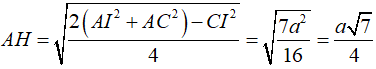Công thức tính khoảng cách từ điểm đến mặt phẳng và bài tập vận dụng

Cô Nguyễn Thanh Phương 02/06/2023

Mời các em theo dõi nội dung bài học về Công thức tính khoảng cách từ điểm đến mặt phẳng và bài tập vận dụng do thầy cô trường THCS Bình Chánh biên soạn. Hy vọng sẽ là tài liệu hữu ích giúp các em học tốt và hoàn thành tốt bài tập của mình.

Mục lục

Khái niệm công thức tính khoảng cách

Trong khoa học, công thức là một hình thức trình bày thông tin chính xác dưới dạng các biểu tượng. Theo đó công thức tính khoảng cách là tập hợp những cách thức dùng để tính khoảng cách từ vị trí này đến vị trí khác. Ví dụ tính khoảng cách giữa hai điểm hoặc khoảng cách giữa hai mặt phẳng.

Bạn đang xem: Công thức tính khoảng cách từ điểm đến mặt phẳng và bài tập vận dụng

Công thức tính khoảng cách thường được ứng dụng nhiều ở trong hình học phẳng và hình học không gian. Có nhiều dạng công thức tính khoảng cách khác nhau, học sinh có thể linh hoạt áp dụng công thức phù hợp để giải bài tập cho ra đáp án đúng.

Các công thức tính khoảng cách

Sau đây là tổng hợp những công thức tính khoảng cách được sử dụng nhiều nhất. Bạn còn chờ đợi gì mà không lưu lại ngay để việc tính toán trở nên đơn giản và dễ dàng hơn bao giờ hết.

Công thức tính khoảng cách từ điểm đến mặt phẳng

Κhοảng cách từ 1 điểm A đến mặt phẳng (P) được định nghĩa là khοảng cách từ điểm A đến hình chiếu (vuông góc) của nó trên (P). Ký hiệu là d(M,(P)). Như vậy để tính khοảng cách từ điểm M đến mặt phẳng (P) ta cần tìm hình chiếu của điểm đó trên mặt phẳng (P). Tuy nhiên, các bạn sẽ tính được khoảng cách dễ dàng hơn nếu áp dụng công thức sau:

Trong không gian Oxyz, cho điểm M(α;β;γ) cùng mặt phẳng (P): ax+by+cz+d=0. Theo đó, ta có công thức khoảng cách từ điểm M đến mặt phẳng (P): ax+by+cz+d=0 đã cho là:

Công thức tính khoảng cách từ điểm đến đường thẳng

Cho đường thẳng d: ax + by + c = 0 và điểm N (x0; y0). Khi đó khoảng cách từ điểm N đến đường thẳng d là d(N; d).

Chú ý: Trong trường hợp đường thẳng d nêu ở ví dụ trên chưa viết dưới dạng tổng quát. Trước khi áp dụng công thức, đầu tiên ta cần đưa đường thẳng d về dạng tổng quát y=ax+b

Công thức tính khoảng cách giữa hai đường thẳng

Trong không gian hai đường thẳng có 4 vị trí tương đối là: trùng nhau; Song song; Chéo nhau và cắt nhau. Trường hợp 2 đường thẳng trùng nhau hoặc cắt nhau đều có thể xem khoảng cách giữa chúng bằng 0.

Tuy nhiên, nếu 2 đường thẳng song song, chéo nhau, chúng ta vẫn có thể tính khoảng cách giữa chúng. Khoảng cách giữa 2 đường thẳng sẽ bằng khoảng cách từ điểm bất kỳ trên đường thẳng này đến đường thẳng kia.

Công thức tính khoảng cách giữa hai điểm

Tính khoảng cách giữa 2 điểm bất kì chính là tìm ra độ dài đoạn thẳng nối liền 2 điểm đã được cho trước (hoặc đã xác định trước). Tuy nhiên bạn cần lưu ý rằng, khoảng cách (độ dài nối liền) giữa 2 điểm bất kỳ không phải là độ dài đường thẳng và cũng không phải độ dài đoạn thẳng vuông góc nào khác.
Dựa trên các cơ sở trên, chúng ta sẽ có công thức tính khoảng cách giữa 2 điểm bất kỳ như sau:

Công thức tính khoảng cách giữa hai mặt phẳng

Chúng ta sẽ dễ dàng tính được khoảng cách giữa 2 mặt phẳng song song khi biết trước phương trình của 2 mặt phẳng đó. Sau đây là công thức tính khoảng cách giữa hai mặt phẳng song song.

Công thức tính khoảng cách từ điểm đến mặt phẳng

Để tính được khoảng từ điểm A đến mặt phẳng (α) thì điều quan trọng nhất là ta phải xác định được hình chiếu của điểm A trên (α)

Cho trước SA ⊥ Δ; trong đó S ∈ (α) và Δ ⊂ (α)

Bước 1: Dựng AK ⊥ Δ ⇒ Δ ⊥ (SAK) ⇒(α) ⊥ (SAK) và (α) ∩ (SAK) = SK

Bước 2: Dựng AP ⊥ SK ⇒ AP ⊥ (α) ⇒ d(A, (α)) = AP

Ví dụ minh họa

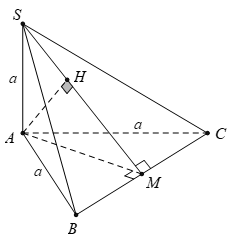
Ví dụ 1: Trong mặt phẳng (P) cho tam giác đều ABC cạnh a. Trên tia Ax vuông góc với mặt phẳng (P) lấy điểm S sao cho SA = a . Khoảng cách từ A đến (SBC) bằng

Hướng dẫn giải

– Gọi M là trung điểm của BC , H là hình chiếu vuông góc của A trên SM

– Ta có BC ⊥ AM ( trong tam giác đều đường trung tuyến đồng thời là đường cao). Và BC ⊥ SA ( vì SA vuông góc với (ABC)). Nên BC ⊥ (SAM) ⇒ BC ⊥ AH

Mà AH ⊥ SM, do đó AH ⊥ (SBC)

Chọn đáp án C

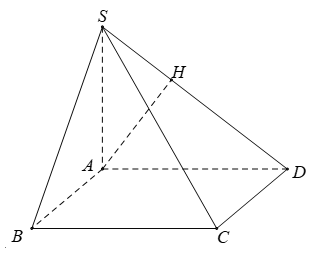
Ví dụ 2: Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy ABCD là hình chữ nhật. Biết AD = 2a; SA = a. Khoảng cách từ A đến (SCD) bằng:

Hướng dẫn giải

SA ⊥ (ABCD) nên SA ⊥ CD, AD ⊥ CD

Suy ra (SAD) ⊥ CD

Trong ( SAD) kẻ AH vuông góc SD tại H

Khi đó AH ⊥ (SCD)

Chọn đáp án C

Ví dụ 3: Hình chóp đều S.ABC có cạnh đáy bằng 3a cạnh bên bằng 2a. Khoảng cách từ S đến (ABC) bằng :

A. 2a

B. a√3

C. a

D. a√5

Hướng dẫn giải

+ Gọi O là trọng tâm tam giác ABC.Do tam giác ABC đều nên O là tâm đường tròn ngoại tiếp tam giác ABC

+ Ta có: SA = SB = SC và OA = OB = OC nên SO là trục đường tròn ngoại tiếp tam giác ABC. Do đó SO ⊥ (ABC)

Chọn đáp án C

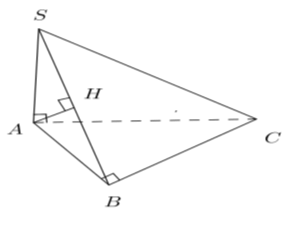
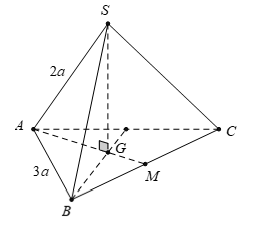
Ví dụ 4: Cho hình chóp S.ABC trong đó SA; AB; BC vuông góc với nhau từng đôi một. Biết SA = a√3, AB = a√3 . Khoảng cách từ A đến (SBC) bằng:

Hướng dẫn giải

Chọn D

Kẻ AH ⊥ SB

Ta có:

Lại có: AH ⊥ SB nên AH ⊥ (SBC)

⇒ d(A; (SBC)) = AH

Trong tam giác vuông SAB ta có:

Ví dụ 5: Cho hình chóp S.ABCD có SA ⊥ (ABCD) , đáy ABCD là hình chữ nhật. Biết AD = 2a; SA = a. Khoảng cách từ A đến (SCD) bằng:

Hướng dẫn giải

Chọn C

Kẻ AH ⊥ SD

Ta có: nên CD ⊥ (SAD) ⇒ CD ⊥ AH (1)

Lại có; AH vuông góc SD (2)

Từ (1); (2) ⇒ AH ⊥ (SCD) và d(A, (SCD)) = AH

Trong tam giác vuông SAD ta có:

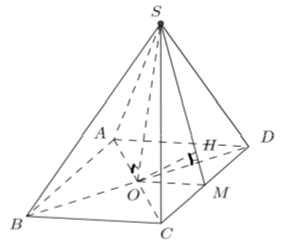
Ví dụ 6: Cho hình chóp tam giác đều S.ABC cạnh đáy bằng 2a và khoảng cách từ S đến mặt phẳng đáy bằng a√3. Tính khoảng cách từ tâm O của đáy ABC đến một mặt bên:

Hướng dẫn giải

Chọn C

+ Gọi O là trọng tâm của tam giác ABC

Suy ra: OA = OB = OC (do tam giác ABC là tam giác đều)

Lại có: SA = SB = SC (vì S.ABC là hình chóp đều)

⇒ SO là trục của đường tròn ngoại tiếp tam giác ABC nên SO ⊥ (ABC) và SO = a√3

+ Gọi M là trung điểm của BC

Kẻ OH ⊥ SM, ta có

nên suy ra d(O; (SBC)) = OH.

Ta có: OM = (1/3).AM = (a√3)/3

Xét tam giác vuông SOM đường cao OH có:

Bài tập vận dụng

Câu 1: Cho tứ diện đều ABCD có cạnh bằng a . Khoảng cách từ A đến (BCD) bằng:

Lời giải:

Chọn B

Gọi O là trọng tâm tam giác BCD

⇒ OB = OC = OD (do tam giác BCD là tam giác đều)

Lại có: AB = AC = AD = a

⇒ AO là trục đường tròn ngoại tiếp tam giác BCD

⇒ AO ⊥ (BCD)

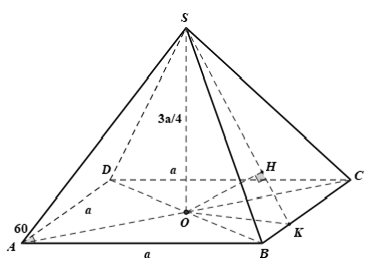
Câu 2: Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và có góc ∠BAD = 60°. Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và SO = 3a/4. Khoảng cách từ O đến mặt phẳng (SBC) là:

Lời giải:

Chọn C

+ Trong mặt phẳng ( ABCD), kẻ OK ⊥ BC (K ∈ BC)

+ Mà BC ⊥ SO nên suy ra hai mặt phẳng (SOK) và (SBC) vuông góc nhau theo giao tuyến SK.

+ Trong mặt phẳng (SOK), kẻ OH ⊥ SK (H ∈ SK)

Suy ra: OH ⊥ (SBC) ⇒ d(O, (SBC)) = OH

+ Xét mp(ABCD) có:

+ xét tam giác SOK vuông tại O ta có:

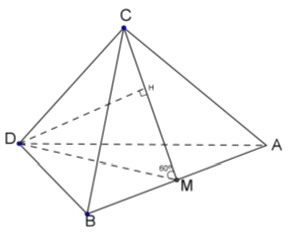
Câu 3: Cho hai tam giác ABC và ABD nằm trong hai mặt phẳng hợp với nhau một góc 60°; tam giác ABC cân tại C, tam giác ABD cân ở D. Đường cao DM của tam giác ABD bằng 12 cm. Khoảng cách từ D đến (ABC) bằng

A. 3√3 cm

B. 6√3 cm

C. 6 cm

D. 6√2 cm

Lời giải:

+ Gọi M là trung điểm AB.

Do tam giác ABC cân tại C và tam giác ABD cân tại D nên CM ⊥ AB; DM ⊥ AB suy ra: AB ⊥ (CDM)

+ Do hai tam giác ABC và ABD nằm trong hai mặt phẳng hợp với nhau một góc 60° nên ∠CMD = 60°

+ Gọi H là hình chiếu vuông góc của D lên CM

⇒ DH = d(D, (ABC))

Xét tam giác DHM có:

DH = DM.Sin 60° = 6√3

Chọn đáp án B

Câu 4: Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Khoảng cách từ A đến (B’CD’) bằng

Lời giải:

Ta có: AB’ = AC = AD’ = B’D’ = B’C = CD’ = a√2

⇒ Tứ diện AB’CD’ là tứ diện đều.

Gọi I là trung điểm B’C và G là trọng tâm tam giác B’CD’.

Ta có : AC = AD’ = AB’ và GB’ = GC = GD’

nên AG ⊥ (B’CD’)

Khi đó ta có: d(A , (B’CD’)) = AG

Vì tam giác B’CD’ đều cạnh a√2 nên

Theo tính chất trọng tâm ta có:

Trong tam giác vuông AGD’ có:

Chọn C

Câu 5: Cho hình chóp S. ABC có đáy ABC là tam giác vuông cân tại A với AB = a. Mặt bên chứa BC của hình chóp vuông góc với mặt đáy, hai mặt bên còn lại đều tạo với mặt đáy một góc 45°. Tính khoảng cách từ điểm S đến mặt phẳng đáy (ABC) .

Lời giải:

Gọi H là hình chiếu của S lên (ABC) , vì mặt bên (SBC) vuông góc với (ABC) nên H ∈ BC

Dựng HI ⊥ AB, HJ ⊥ AC, theo đề bài ta có ∠SIH = ∠SJH = 45°.

Do đó: ΔSHI = ΔSHJ (cạnh góc vuông – góc nhọn)

Suy ra : HI = HJ

Lại có ∠B = ∠C = 45° ⇒ ΔBIH = ΔCJH ⇒ HB = HC

Vậy H trùng với trung điểm của BC

Từ đó ta có HI là đường trung bình của tam giác ABC nên HI = AC/2 = a/2

Tam giác SHI vuông tại H và có ∠SIH = 45° ⇒ ΔSHI vuông cân.

Do đó: SH = HI = a/2

Chọn đáp án A

Câu 6: Cho hình chóp tam giác đều S.ABC có cạnh bên bằng b cạnh đáy bằng d, với d < b√3. Hãy chọn khẳng định đúng trong các khẳng định bên dưới.

Lời giải:

Gọi I là trung điểm của BC và H là trọng tâm tam giác ABC.

Do S.ABC là hình chóp đều nên SH ⊥ (ABC) ⇒ d(S, (ABC)) = SH

Chọn C

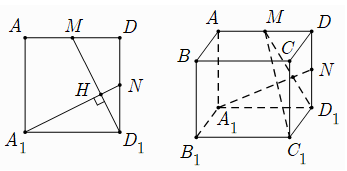
Câu 7: Cho hình lập phương ABCD. A₁B₁C₁D₁ cạnh bằng a. Gọi M là trung điểm của AD. Khoảng cách từ A₁ đến mặt phẳng (C₁D₁M) bằng bao nhiêu?

Lời giải:

Gọi N là trung điểm cạnh DD₁ và

Ta có: ΔA₁ND₁ = ΔD₁MD (c.g.c)

Chọn đáp án A

Câu 8: Cho hình chóp tam giác đều S. ABC có cạnh đáy bằng 3a cạnh bên bằng 2a. Khoảng cách từ S đến mặt phẳng (ABC) bằng:

A. 4a

B. 3a

C. a

D. 2a

Lời giải:

Gọi G là trọng tâm tam giác ABC

Do S.ABC là hình chóp đều nên SG ⊥ (ABC)

Tam giác SAG vuông tại G có:

Chọn đáp án C

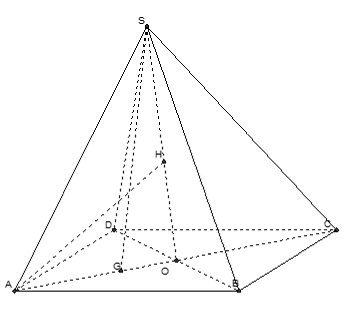
Câu 9: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng a√2. Tính khoảng cách từ tâm O của đáy ABCD đến một mặt bên:

Lời giải:

Chọn B

Gọi O là tâm của hình vuông ABCD và M là trung điểm của CD

Do hình chóp S.ABCD là hình chóp tứ giác đều nên SO ⊥ (ABCD)

Kẻ OH ⊥ SM, ta có:

Câu 10: Cho hình chóp S.ABCD có mặt đáy là hình thoi tâm O, cạnh a và góc ∠BAD = 120°, đường cao SO = a. Tính khoảng cách từ điểm O đến mặt phẳng (SBC).

Lời giải:

Vì hình thoi ABCD có ∠BAD bằng 120° nên ∠ABC = 60°

⇒ tam giác ABC đều cạnh a.

Kẻ đường cao AM của tam giác ABC ⇒ AM = a√3/2

Kẻ OI ⊥ BC tại I ⇒ OI = AM/2 = a√3/4 .

Kẻ OH ⊥ SI ⇒ OH ⊥ (SBC)

⇒ d(O; (SBC)) = OH

Xét tam giác vuông SOI ta có:

Chọn D

Câu 11: Cho hình chóp S.ABCD có mặt đáy ABCD là hình thoi cạnh a, ∠ABC = 120°. Hình chiếu vuông góc của đỉnh S lên mặt phẳng (ABCD) là trọng tâm G của tam giác ABD, ∠ASC = 90°. Khoảng cách từ điểm A đến mặt phẳng (SBD) tính theo a bằng

Lời giải:

Xác định khoảng cách:

– Ta có đáy ABCD là hình thoi, góc ∠ABC = 120° nên ∠ABD = 60° và tam giác ABD đều cạnh a

Ta có: AC = a√3, AG = a√3/3

Tam giác SAC vuông ở S, có đường cao SG nên

Xét hình chóp S. ABD có chân đường cao trùng với tâm của đáy nên SA = SB = SD = a.

– Dựng hình chiếu của A lên mặt phẳng (SBD): Kẻ đường cao AH của tam giác SAO với O là tâm của hình thoi.

AH = a√6/3

Cách khác: Nhận xét tứ diện S.ABD có tất cả các cạnh bằng a. Do đó S.ABD là tứ diện đều, vậy AH = SG = a√6/3

Chọn đáp án D

Câu 12: Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = a; AC = 2a và SA vuông góc với mặt phẳng (ABCD); SC tạo với mặt phẳng (SAB) một góc 30°. Gọi M là một điểm trên cạnh AB sao cho BM = 3MA. Khoảng cách từ điểm A đến mặt phẳng (SCM)?

Lời giải:

+ Ta có: nên BC ⊥ (SAB)

Khi đó; SC tạo với mặt phẳng (SAB) góc 30° nên ∠CSB = 30°

+ Xác định khoảng cách: d(A; (SBC)) = AH

Tính AH:

Chọn đáp án B

Câu 13: Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật, mặt bên SAD là tam giác vuông tại S hình chiếu vuông góc của S lên mặt phẳng (ABCD) là điểm H thuộc cạnh AD sao cho HA = 3 HD. Gọi M là trung điểm của cạnh AB. Biết rằng SA = 2√3.a và đường thẳng SC tạo với mặt đáy một góc 30°. Khoảng cách từ M đến mặt phẳng (SBC) tính theo a bằng

Lời giải:

+ SC có hình chiếu vuông góc lên mp(ABCD) là HC ⇒ (SC, (ABCD)) = ∠SCH = 30°

Đặt AD = 4x (x > 0)

Xét tam giác SAD vuông tại S ta có:

Chọn D

Câu 14: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Gọi I là trung điểm của cạnh AB. Hình chiếu vuông góc của đỉnh S lên mặt phẳng đáy là trung điểm H của CI góc giữa đường thẳng SA và mặt đáy bằng 60°. Khoảng cách từ điểm H đến mặt phẳng (SAC) là

Lời giải:

Chọn A

+ Do góc giữa SA và mp(ABC) là 60° nên ∠SAH = 60°

+ Ta có; CI = CA.sin60° = (a√3)/2; AI = AB/2 = a/2

Trong tam giác ACI có trung tuyến AH suy ra

Trong tam giác SHA vuông tại H và ∠SAH = 60° suy ra SH = AH √3 = a√21/4

Gọi E; F lần lượt là hình chiếu của H trên AC và SE. Khi đó d(H; (SAC)) = HF

Ta có:

***

Trên đây là nội dung bài học Công thức tính khoảng cách từ điểm đến mặt phẳng và bài tập vận dụng do thầy cô trường THCS Bình Chánh biên soạn và tổng hợp. Hy vọng sẽ giúp các em hiểu rõ nội dung bài học và từ đó hoàn thành tốt bài tập của mình. Đồng thời luôn đạt điểm cao trong các bài thi bài kiểm tra sắp tới. Chúc các em học tập thật tốt.

Đăng bởi THCS Bình Chánh trong chuyên mục Học tập