Học Tập Lớp 10 Toán 10 Chân trời sáng tạo

Giải Bài 6 trang 119 Toán 10 tập 1 SGK Chân trời sáng tạo

Trường THCS Bình Chánh 24/07/2023

Mời các em theo dõi nội dung bài học do thầy cô trường THCS Bình Chánh biên soạn sẽ giúp các em nắm chắc kiến thức nội dung bài học tốt hơn.

Mục lục

Bài 6 trang 119 SGK Toán 10

Toán lớp 10 Bài 6 trang 119 là lời giải bài Các số đặc trưng đo xu thế trung tâm của mẫu số liệu SGK Toán 10 sách Chân trời sáng tạo hướng dẫn chi tiết lời giải giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 10. Mời các em học sinh cùng tham khảo chi tiết.

Giải bài 6 Toán 10 trang 119

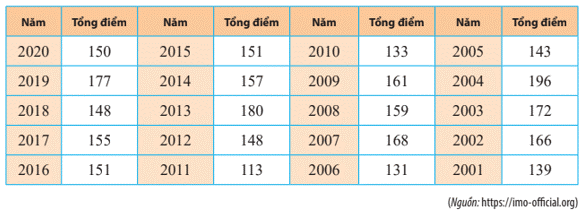
Bài 6 (SGK trang 119): Tổng số điểm mà các thành viên đội tuyển Olympic Toán quốc tế (IMO) của Việt Nam đạt được trong 20 kì thi được cho ở bảng sau:

Bạn đang xem: Giải Bài 6 trang 119 Toán 10 tập 1 SGK Chân trời sáng tạo

Có ý kiến cho rằng điểm thi của đội tuyển giai đoạn 2001 – 2010 cao hơn giai đoạn 2011 – 2020. Hãy sử dụng số trung bình và trung vị để kiểm nghiệm xem ý kiến trên có đúng không?

Hướng dẫn giải

– Để tìm trung vị của một mẫu số liệu, ta thực hiện như sau:

+ Sắp xếp các giá trị trong mẫu số liệu theo thứ tự không giảm.

+ Nếu số giá trị của mẫu số liệu là số lẻ thì giá trị chính giữa của mẫu là trung vị. Nếu là số chẵn thì trung vị là trung bình cộng của hai giá trị chính giữa của mẫu.

– Để tìm các tứ phân vị của mẫu số liệu có n giá trị ta làm như sau:

+ Sắp xếp mẫu số liệu theo thứ tự không giảm.

+ Tìm trung vị. Giá trị này là Q₂

+ Tìm trung vị của nửa số liệu bên trái Q₂ (không bao gồm Q₂ nếu n lẻ) Giá trị này là Q₁

+ Tìm trung vị của nửa số liệu bên phải Q₂ (không bao gồm Q₂ nếu n lẻ). Giá trị này là Q₃

Lời giải chi tiết

Trong giai đoạn từ năm 2001 đến năm 2010:

Cỡ mẫu là n₁ = 10.

Số trung bình:

$\overline x = \frac{{139 + 166 + 172 + 196 + 143 + 131 + 168 + 159 + 161 + 133}}{{10}} = 156,8$

Sắp xếp các số liệu theo thứ tự không giảm ta được:

131; 133; 139; 143; 159; 161; 166; 168; 172; 196.

Vì cỡ mẫu là số chẵn nên số trung vị là: $\frac{1}{2}\left( {159 + 161} \right) = 160$

Trong giai đoạn từ năm 2011 đến năm 2020:

Cỡ mẫu là n₂ = 10

Số trung bình: $\overline x = \frac{{113 + 148 + 180 + 157 + 151 + 151 + 155 + 148 + 177 + 150}}{{10}} = 153$

Sắp xếp các số liệu theo thứ tự không giảm, ta được:

113; 148; 148; 150; 151; 151; 155; 157; 177; 180.

Vì cỡ mẫu là số chẵn nên số trung vị là $\frac{1}{2}\left( {151 + 151} \right) = 151$

+ Nếu dựa theo số trung bình, ta có: 156,8 > 153 => Điểm thi của đội tuyển giai đoạn 2001 – 2010 cao hơn giai đoạn 2011 – 2020.

+ Nếu dựa theo số trung vị, ta có: 160 > 151 nên điểm thi của đội tuyển giai đoạn 2001 – 2010 cao hơn giai đoạn 2011 – 2020.

Vậy dựa vào cả số trung vị và số trung bình, ta thấy rằng ý kiến đã cho đúng.

—–> Câu hỏi cùng bài tiếp theo: Bài 7 trang 119 SGK Toán 10

—————————————-

Trên đây là lời giải chi tiết Bài 6 Toán lớp 10 trang 119 Các số đặc trưng đo xu thế trung tâm của mẫu số liệu cho các em học sinh tham khảo, nắm được cách giải các dạng toán của Chương 6: Thống kê. Hi vọng đây là tài liệu hữu ích cho các bạn ôn tập kiểm tra năng lực, bổ trợ cho quá trình học tập trong chương trình THPT cũng như ôn luyện cho kì thi THPT Quốc gia. Chúc các bạn học tốt!

Đăng bởi: THCS Bình Chánh

Chuyên mục: Toán 10 Chân trời sáng tạo