Học Tập Lớp 10 Toán 10 Chân trời sáng tạo

Giải Toán 10 Bài 3 Chân trời sáng tạo: Tích của một số với một vectơ | Giải Toán lớp 10

Trường THCS Bình Chánh 24/07/2023

Mời các em theo dõi nội dung bài học do thầy cô trường Trung học Bình Chánh biên soạn sẽ giúp các em nắm chắc kiến thức nội dung bài học tốt hơn.

Giải bài tập Toán 10 Bài 3: Tích của một số với một vectơ

1. Tích của một số với một vectơ và các tính chất

Bạn đang xem: Giải Toán 10 Bài 3 Chân trời sáng tạo: Tích của một số với một vectơ | Giải Toán lớp 10

Giải Toán 10 trang 94 Tập 1

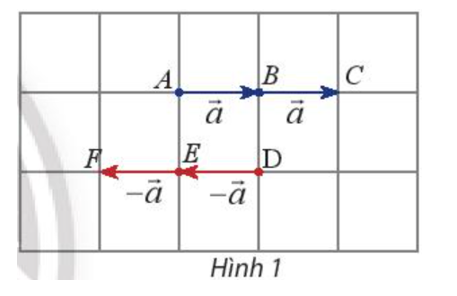
Hoạt động khám phá 1 trang 94 Toán lớp 10 Tập 1: Cho vectơ $\vec{a}$ . Hãy xác định độ dài và hướng của hai vectơ $\vec{a} + \vec{a}, (- \vec{a}) + (- \vec{a})$ (Hình 1).

Lời giải:

Vectơ $\vec{a} + \vec{a}$ có hướng từ A sang C.

Vectơ $(- \vec{a}) + (- \vec{a})$ có hướng từ D sang F.

Giải Toán 10 trang 95 Tập 1

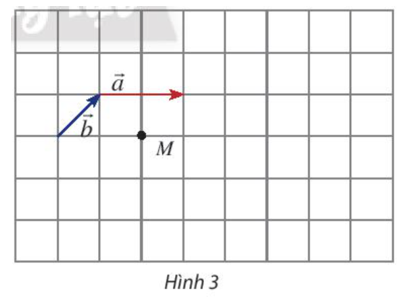
Thực hành 1 trang 95 Toán lớp 10 Tập 1: Cho hai vectơ $\vec{a}, \vec{b}$ và một điểm M như Hình 3.

a) Hãy vẽ các vectơ $\vec{M N} = 3 \vec{a}, \vec{M P} = - 3 \vec{b}$ .

b) Cho biết mỗi ô vuông có cạnh bằng 1. Tính: $|3 \vec{b}|, |- 3 \vec{b}|, |2 \vec{a} + 2 \vec{b}|$ .

Lời giải:

a) Ta thấy 3 > 0 nên hai vectơ $\vec{M N}$ và $\vec{a}$ cùng hướng.

Do đó từ M kẻ đường thẳng d song song với đường thẳng a.

Trên đường thẳng d, về bên phải điểm M chọn điểm N sao cho MN = 6.

Khi đó $\vec{M N} = 3 \vec{a}$ .

Do -3 < 0 nên hai vectơ $\vec{M P}$ và $\vec{b}$ ngược hướng.

Do đó từ M kẻ đường thẳng c song song với đường thẳng b.

Trên đường thẳng c, về bên trái điểm M chọn P sao cho MP = 3.

Khi đó $\vec{M P} = - 3 \vec{b}$ .

Ta có hình vẽ như sau:

b) Ta thấy MP là độ dài cạnh huyền của 1 tam giác vuông cân có cạnh bằng 3.

Do đó MP = $\sqrt{3^{2} + 3^{2}} = 3 \sqrt{2}$ .

Ta thấy $3 \vec{b}$ và $- 3 \vec{b}$ là hai vectơ đối nên $|3 \vec{b}| = |- 3 \vec{b}| = |\vec{M P}| = 3 \sqrt{2}$ .

Ta thấy $|\vec{b} + \vec{a}|$ là độ cạnh huyền của 1 tam giác vuông có độ dài 2 cạnh góc vuông lần lượt là 1 và 3.

Khi đó $|\vec{b} + \vec{a}| = \sqrt{3^{2} + 1^{2}} = \sqrt{10}$ .

Do đó $|2 \vec{b} + 2 \vec{a}| = |2 \vec{a} + 2 \vec{b}| = 2 \sqrt{10}$ .

Vậy $|3 \vec{b}| = |- 3 \vec{b}| = 3 \sqrt{2}$ ; $|2 \vec{a} + 2 \vec{b}| = 2 \sqrt{10}$ .

Thực hành 2 trang 95 Toán lớp 10 Tập 1: Cho tam giác ABC. Chứng minh G là trọng tâm của tam giác ABC khi và chỉ khi $\vec{M A} + \vec{M B} + \vec{M C} = 3 \vec{M G}$ .

Lời giải:

Phần thuận: G là trọng tâm của tam giác ABC thì $\vec{M A} + \vec{M B} + \vec{M C} = 3 \vec{M G}$ .

Chứng minh:

Do G là trọng tâm của tam giác ABC nên $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$ .

Do đó $\vec{M G} + \vec{G A} + \vec{M G} + \vec{G B} + \vec{M G} + \vec{G C} = 3 \vec{M G}$ hay $\vec{M A} + \vec{M B} + \vec{M C} = 3 \vec{M G}$ .

Phần đảo: Tam giác ABC có $\vec{M A} + \vec{M B} + \vec{M C} = 3 \vec{M G}$ thì G là trọng tâm của tam giác ABC.

Chứng minh:

$\vec{M A} + \vec{M B} + \vec{M C} = 3 \vec{M G}$

$\Rightarrow \vec{M G} + \vec{G A} + \vec{M G} + \vec{G B} + \vec{M G} + \vec{G C} = 3 \vec{M G}$

$\Rightarrow \vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$

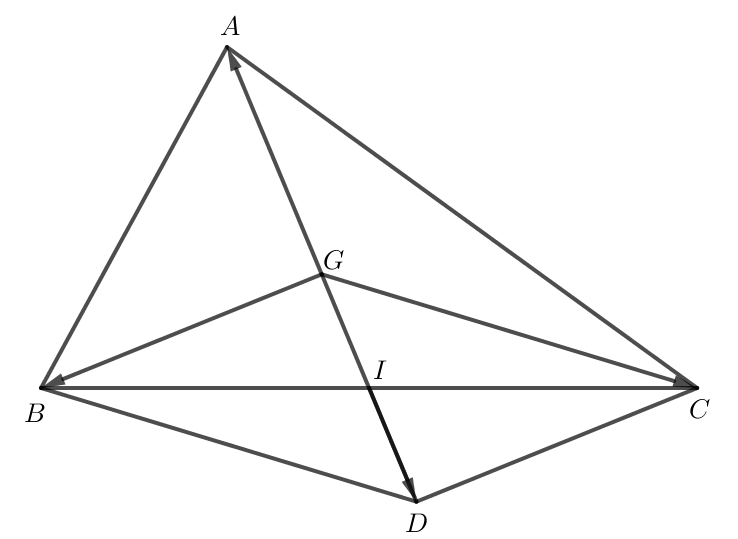
Dựng hình bình hành GBDC và gọi I là giao điểm của GD và BC.

Áp dụng quy tắc hình bình hành ta có $\vec{G B} + \vec{G C} = \vec{G D}$ .

Mà $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$ hay $\vec{G A} + \vec{G D} = \vec{0}$ .

Do đó $\vec{G A} = - \vec{G D}$ .

Khi đó $|\vec{G A}| = |- \vec{G D}|$ hay GA = GD.

Hình bình hành GBDC có I là giao điểm hai đường chéo GD và BC nên I là trung điểm của BC và I là trung điểm của GD.

Do I là trung điểm của GD nên GI = $\frac{1}{2}$ GD = $\frac{1}{2}$ GA.

GI = $\frac{1}{2}$ GA nên AI = GI + GA = $\frac{1}{2}$ GA + GA = $\frac{3}{2}$ GA hay AG = $\frac{2}{3}$ AI.

Tam giác ABC có AI là đường trung tuyến, lại có AG = $\frac{2}{3}$ AI nên G là trọng tâm của tam giác ABC.

Vậy ta có điều phải chứng minh.

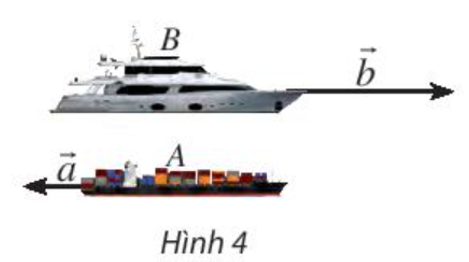
Vận dụng trang 95 Toán lớp 10 Tập 1: Một con tàu chở hàng A đang đi về hướng tây với tốc độ 20 hải lí/giờ. Cùng lúc đó, một con tàu chở khách B đang đi về hướng đông với tốc độ 50 hải lí/giờ. Biểu diễn vectơ vận tốc $\vec{b}$ của tàu B theo vectơ vận tốc $\vec{a}$ của tàu A.

Lời giải:

Ta thấy hai vectơ $\vec{a}$ và $\vec{b}$ ngược hướng và $|\vec{b}| = 50; |\vec{a}| = 20$ .

$\Rightarrow |\vec{b}| = \frac{5}{2} |\vec{a}|$ .

Vậy $\vec{b} = \frac{- 5}{2} \vec{a}$ .

2. Điều kiện để hai vectơ cùng phương

Giải Toán 10 trang 96 Tập 1

Hoạt động khám phá 2 trang 96 Toán lớp 10 Tập 1: Cho hai vectơ $\vec{a}$ và $\vec{b}$ cùng phương, $\vec{b}$ khác $\vec{0}$ và cho $\vec{c} = \frac{|\vec{a}|}{|\vec{b}|} . \vec{b}$ . So sánh độ dài và hướng của hai vectơ $\vec{a}$ và $\vec{c}$ .

Lời giải:

Ta thấy với $\vec{b}$ khác $\vec{0}$ thì $\frac{|\vec{a}|}{|\vec{b}|}$ ≥ 0.

Do đó hai vectơ $\vec{c}$ và $\vec{b}$ là hai vectơ cùng hướng.

Mà $\vec{a}$ và $\vec{b}$ là hai vectơ cùng phương nên hai vectơ $\vec{a}$ và $\vec{c}$ cùng hướng khi hai vectơ $\vec{a}$ và $\vec{b}$ cùng hướng; hai vectơ $\vec{a}$ và $\vec{c}$ ngược hướng khi hai vectơ $\vec{a}$ và $\vec{b}$ ngược hướng.

Do $\vec{c} = \frac{|\vec{a}|}{|\vec{b}|} . \vec{b}$ nên $|\vec{c}| = |\frac{|\vec{a}|}{|\vec{b}|} . \vec{b}| = \frac{|\vec{a}|}{|\vec{b}|} . |\vec{b}| = |\vec{a}|$ .

Do đó độ dài của hai vectơ $\vec{a}$ và $\vec{c}$ bằng nhau.

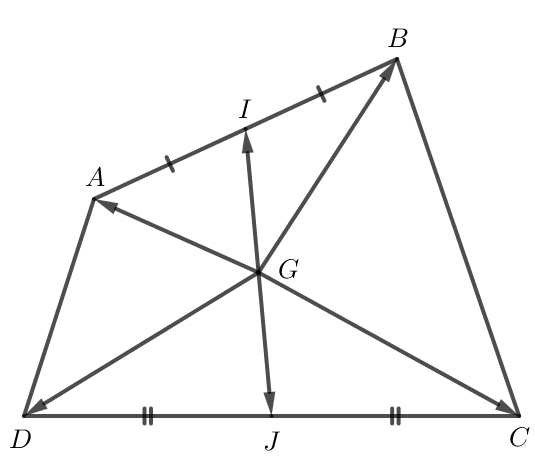
Thực hành 3 trang 96 Toán lớp 10 Tập 1: Cho tứ giác ABCD có I và J lần lượt là trung điểm của AB và CD. Cho điểm G thỏa mãn $\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D} = \vec{0}$ . Chứng minh ba điểm I, G, J thẳng hàng.

Lời giải:

Do I là trung điểm của AB nên $\vec{G A} + \vec{G B} = 2 \vec{G I}$ .

Do J là trung điểm của CD nên $\vec{G C} + \vec{G D} = 2 \vec{G J}$ .

Do đó $\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D} = 2 \vec{G I} + 2 \vec{G J}$ hay $\vec{G I} + \vec{G J} = \vec{0}$ .

Do $\vec{G I} + \vec{G J} = \vec{0}$ nên G là trung điểm của IJ.

Vậy I, G, J thẳng hàng.

Bài tập

Giải Toán 10 trang 97 Tập 1

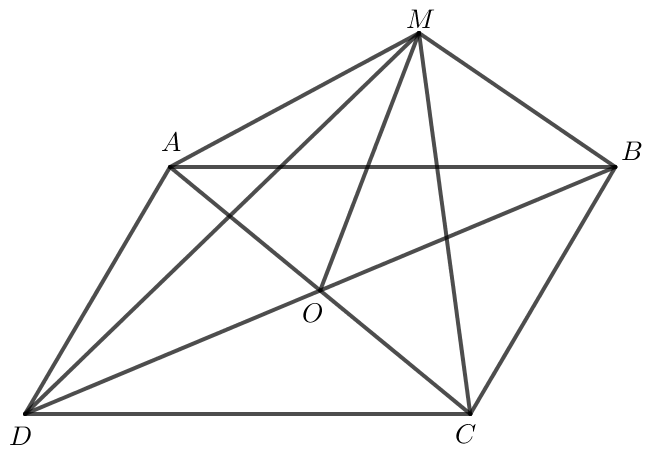
Bài 1 trang 97 Toán lớp 10 Tập 1: Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Với M là điểm tùy ý, chứng minh rằng:

a) $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 4 \vec{M O}$ ;

b) $\vec{A B} + \vec{A C} + \vec{A D} = 2 \vec{A C}$ .

Lời giải:

a) Hình bình hành ABCD có O là giao điểm hai đường chéo nên OA = OC, OB = OD.

Khi đó $\vec{O A}$ và $\vec{O C}$ là hai vectơ đối, $\vec{O B}$ và $\vec{O D}$ là hai vectơ đối.

Do đó $\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} = \vec{0}$ .

Ta có

$\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = \vec{M O} + \vec{O A} + \vec{M O} + \vec{O B} + \vec{M O} + \vec{O C} + \vec{M O} + \vec{O D}$

$= 4 \vec{M O} + (\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D})$

$= 4 \vec{M O}$

Vậy $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 4 \vec{M O}$ .

b) Áp dụng quy tắc hình bình hành ta có $\vec{A B} + \vec{A D} = \vec{A C}$ .

Do đó $\vec{A B} + \vec{A D} + \vec{A C} = \vec{A C} + \vec{A C}$ hay $\vec{A B} + \vec{A C} + \vec{A D} = 2 \vec{A C}$ .

Vậy $\vec{A B} + \vec{A C} + \vec{A D} = 2 \vec{A C}$ .

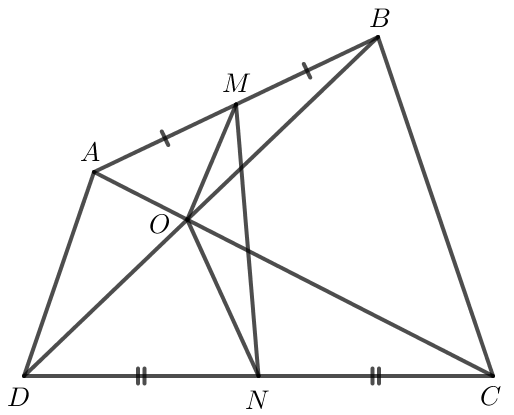
Bài 2 trang 97 Toán lớp 10 Tập 1: Cho tứ giác ABCD. Gọi M và N lần lượt là trung điểm của các cạnh AB và CD. Chứng minh rằng:

a) $\vec{A C} + \vec{B D} = 2 \vec{M N}$ ;

b) $\vec{A C} + \vec{B D} = \vec{B C} + \vec{A D}$ .

Lời giải:

a) Gọi O là giao điểm hai đường chéo của tứ giác ABCD.

Do M là trung điểm của AB nên $\vec{O A} + \vec{O B} = 2 \vec{O M}$ .

Do đó $\vec{A O} + \vec{B O} = 2 \vec{M O}$ .

Do N là trung điểm của CD nên $\vec{O C} + \vec{O D} = 2 \vec{O N}$ .

Do đó $\vec{A O} + \vec{B O} + \vec{O C} + \vec{O D} = 2 \vec{M O} + 2 \vec{O N}$ .

hay $\vec{A O} + \vec{O C} + \vec{B O} + \vec{O D} = 2 \vec{M N}$ .

Do đó $\vec{A C} + \vec{B D} = 2 \vec{M N}$ .

b) Ta có $\vec{A D} = \vec{A C} + \vec{C D}$

Do đó

$\vec{B C} + \vec{A D} = \vec{B C} + \vec{A C} + \vec{C D} = \vec{A C} + (\vec{B C} + \vec{C D}) = \vec{A C} + \vec{B D}$ .

Vậy $\vec{A C} + \vec{B D} = \vec{B C} + \vec{A D}$ .

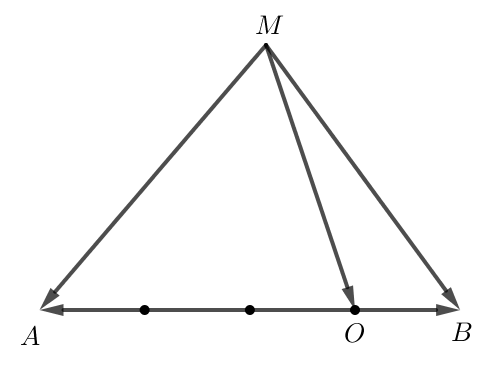
Bài 3 trang 97 Toán lớp 10 Tập 1: Cho hai điểm phân biệt A và B. Xác định điểm M sao cho $\vec{M A} + 4 \vec{M B} = \vec{0}$ .

Lời giải:

Do $\vec{M A} + 4 \vec{M B} = \vec{0}$ nên $\vec{M A} = - 4 \vec{M B}$ do đó $|\vec{M A}| = |- 4| |\vec{M B}| = 4 |\vec{M B}|$ hay MA = 4MB.

Ta thấy -4 < 0 nên hai vectơ $\vec{M A}$ và $\vec{M B}$ ngược hướng.

Do đó A và B nằm ở hai phía so với điểm M.

Ta thực hiện vẽ như sau:

Bước 1. Vẽ đường thẳng d, trên đường thẳng d xác định hai điểm M và B.

Bước 2. Trên đường thẳng d, xác định điểm A sao cho A và B nằm ở hai phía so với điểm M thỏa mãn MA = 4MB.

Ta có hình vẽ như sau:

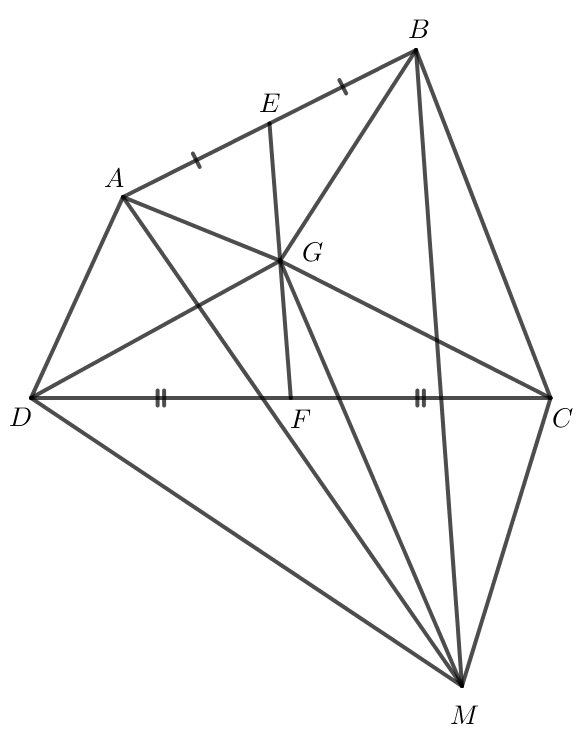
Bài 4 trang 97 Toán lớp 10 Tập 1: Cho tứ giác ABCD. Gọi E, F, G lần lượt là trung điểm của các đoạn thẳng AB, CD, EF. Lấy điểm M tùy ý, chứng minh rằng $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 4 \vec{M G}$ .

Lời giải:

Do E là trung điểm của AB nên $\vec{G A} + \vec{G B} = 2 \vec{G E}$ .

Do F là trung điểm của CD nên $\vec{G C} + \vec{G D} = 2 \vec{G F}$ .

Do G là trung điểm của EF nên $\vec{G E} + \vec{G F} = \vec{0}$ .

Do đó $\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D} = 2 \vec{G E} + 2 \vec{G F} = 2 (\vec{G E} + \vec{G F}) = \vec{0}$ .

Ta có

$\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = \vec{M G} + \vec{G A} + \vec{M G} + \vec{G B} + \vec{M G} + \vec{G C} + \vec{M G} + \vec{G D}$

$= 4 \vec{M G} + (\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D})$

$= 4 \vec{M G}$

Vậy $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 4 \vec{M G}$ .

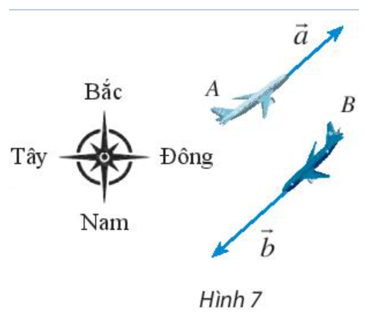
Bài 5 trang 97 Toán lớp 10 Tập 1: Máy bay A đang bay về hướng đông bắc với tốc độ 600 km/h. Cùng lúc đó, máy bay B đang bay về hướng tây nam với tốc độ 800 km/h. Biểu diễn vectơ vận tốc $\vec{b}$ của máy bay B theo vectơ vận tốc $\vec{a}$ của máy bay A.

Lời giải:

Ta thấy hai vectơ $\vec{a}$ và $\vec{b}$ ngược hướng và $|\vec{a}|$ = 600, $|\vec{b}|$ = 800.

Do đó $|\vec{b}| = \frac{800}{600} |\vec{a}| = \frac{4}{3} |\vec{a}|$ hay b = $\frac{4}{3}$ a.

Mà hai vectơ $\vec{a}$ và $\vec{b}$ ngược hướng nên $\vec{b} = - \frac{4}{3} \vec{a}$ .

Vậy $\vec{b} = - \frac{4}{3} \vec{a}$ .

Bài 6 trang 97 Toán lớp 10 Tập 1: Cho hai điểm phân biệt A và B.

a) Xác định điểm O sao cho $\vec{O A} + 3 \vec{O B} = \vec{0}$ .

b) Chứng minh rằng với mọi điểm M, ta có $\vec{M A} + 3 \vec{M B} = 4 \vec{M O}$ .

Lời giải:

a) Do $\vec{O A} + 3 \vec{O B} = \vec{0}$ nên $\vec{O A} = - 3 \vec{O B}$ do đó $|\vec{O A}| = |- 3| |\vec{O B}| = 3 |\vec{O B}|$ hay OA = 3OB.

Ta thấy -3 < 0 nên hai vectơ $\vec{O A}$ và $\vec{O B}$ ngược hướng.

Do đó A và B nằm ở hai phía so với điểm O.

Ta thực hiện vẽ như sau:

Bước 1. Vẽ đường thẳng d, trên đường thẳng d xác định hai điểm O và B.

Bước 2. Trên đường thẳng d, xác định điểm A sao cho A và B nằm ở hai phía so với điểm O thỏa mãn OA = 3OB.

Ta có hình vẽ như sau:

Ta có

$\vec{M A} + 3 \vec{M B} = \vec{M O} + \vec{O A} + 3 (\vec{M O} + \vec{O B}) = 4 \vec{M O} + \vec{O A} + 3 \vec{O B} = 4 \vec{M O}$ .

Vậy $\vec{M A} + 3 \vec{M B} = 4 \vec{M O}$ .

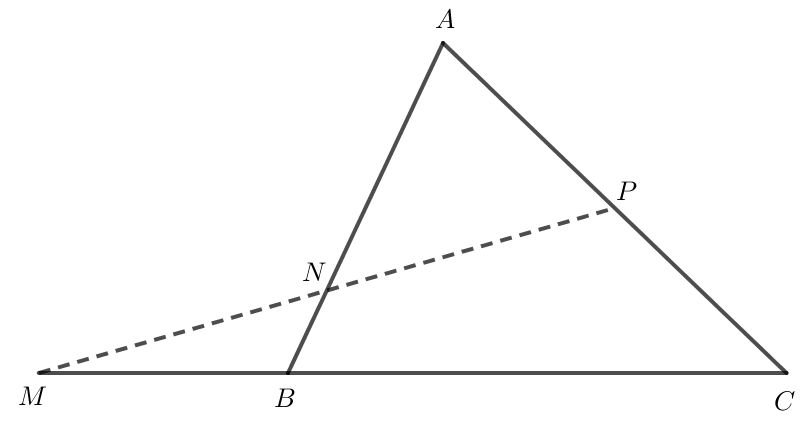
Bài 7 trang 97 Toán lớp 10 Tập 1: Cho tam giác ABC.

a) Xác định các điểm M, N, P thỏa mãn: $\vec{M B} = \frac{1}{2} \vec{B C}, \vec{A N} = 3 \vec{N B}, \vec{C P} = \vec{P A}$ .

b) Biểu thị mỗi vectơ $\vec{M N}, \vec{M P}$ theo hai vectơ $\vec{B C}, \vec{B A}$ .

c) Chứng minh ba điểm M, N, P thẳng hàng.

Lời giải:

a) Do $\vec{M B} = \frac{1}{2} \vec{B C}$ nên hai vectơ $\vec{M B}$ và $\vec{B C}$ cùng hướng.

Do đó M và C nằm ở hai phía so với điểm B sao cho MB = $\frac{1}{2}$ BC.

Do $\vec{A N} = 3 \vec{N B}$ nên $\vec{A N} + \vec{N B} = 4 \vec{N B}$ hay $\vec{A B} = 4 \vec{N B}$ .

Do đó A và N nằm cùng phía so với điểm B sao cho NB = $\frac{1}{4}$ AB.

Do $\vec{C P} = \vec{P A}$ nên $\vec{C P} + \vec{P A} = 2 \vec{P A}$ hay $\vec{C A} = 2 \vec{P A}$ .

Do đó P và C nằm cùng phía so với điểm A sao cho PA = $\frac{1}{2}$ CA.

Ta có hình vẽ sau:

b) Ta có $\vec{M N} = \vec{B N} - \vec{B M}$ .

Do $\vec{A N} = 3 \vec{N B}$ nên $\vec{N A} = 3 \vec{B N} \Rightarrow \vec{B N} + \vec{N A} = 4 \vec{B N}$ hay $\vec{B A} = 4 \vec{B N}$ .

Do đó $\vec{B N} = \frac{1}{4} \vec{B A}$ .

Do $\vec{M B} = \frac{1}{2} \vec{B C}$ nên $\vec{B M} = \frac{- 1}{2} \vec{B C}$ .

Do đó $\vec{M N} = \vec{B N} - \vec{B M} = \frac{1}{4} \vec{B A} + \frac{1}{2} \vec{B C}$ .

Ta có $\vec{M P} = \vec{B P} - \vec{B M}$ .

Do đó P và C nằm cùng phía so với điểm A và PA = $\frac{1}{2}$ CA nên P là trung điểm của CA.

Do đó $\vec{B A} + \vec{B C} = 2 \vec{B P} \Rightarrow \vec{B P} = \frac{1}{2} (\vec{B A} + \vec{B C})$ .

Do đó $\vec{M P} = \vec{B P} - \vec{B M} = \frac{1}{2} (\vec{B A} + \vec{B C}) + \frac{1}{2} \vec{B C} = \frac{1}{2} \vec{B A} + \vec{B C}$ .

Ta thấy $\vec{M N} = \frac{1}{4} \vec{B A} + \frac{1}{2} \vec{B C}$ ; $\vec{M P} = \frac{1}{2} \vec{B A} + \vec{B C}$ nên $\vec{M P} = 2 \vec{M N}$ .

Do đó M, N, P thẳng hàng và N là trung điểm của MP.

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 4: Tích vô hướng của hai vectơ

Bài tập cuối chương 5

Bài 1: Số gần đúng và sai số

Bài 2: Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ

Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu

Xem thêm tài liệu Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 3: Tích của một số với một vectơ

Đăng bởi: THCS Bình Chánh

Chuyên mục: Toán 10 Chân trời sáng tạo

Rate this post

Trường THCS Bình Chánh 24/07/2023

Bài viết liên quan

Để lại một bình luận Hủy