Giải Toán 7 Chân trời sáng tạo: Bài tập cuối chương 9
Mời các em theo dõi nội dung bài học do thầy cô trường Trung học Bình Chánh biên soạn sẽ giúp các em nắm chắc kiến thức nội dung bài học tốt hơn.
Giải bài tập Toán 7 Bài tập cuối chương 9
Giải Toán 7 trang 96 Tập 2
Bạn đang xem: Giải Toán 7 Chân trời sáng tạo: Bài tập cuối chương 9
Bài 1 trang 96 Toán 7 Tập 2:
Trên giá sách có 3 quyển truyện tranh và 1 quyển sách giáo khoa. An chọn ngẫu nhiên 2 quyển từ giá sách. Trong các biến cố sau, hãy chỉ ra biến cố nào là chắc chắn, không thể, ngẫu nhiên. Tại sao?
A: “An chọn được 2 quyển truyện tranh”;
B: “An chọn được ít nhất 1 quyển truyện tranh”;
C: “An chọn được 2 quyển sách giáo khoa”.
Lời giải:
• Xét biến cố A: “An chọn được 2 quyển truyện tranh”.
Biến cố A xảy ra nếu trong 2 quyển được chọn có 2 quyển truyện tranh, biến cố A không xảy ra nếu chẳng hạn trong 2 quyển được chọn có 1 quyển sách giáo khoa.
Do đó biến cố A là biến cố ngẫu nhiên.
• Xét biến cố B: “An chọn được ít nhất 1 quyển truyện tranh”.
Vì chỉ có 1 quyển sách giáo khoa nên trong 2 quyển sách lấy ra từ giá thì có nhiều nhất 1 quyển sách giáo khoa.
Khi đó, An luôn chọn được ít nhất 1 quyển truyện tranh.
Do đó biến cố B là biến cố chắc chắn.
• Xét biến cố C: “An chọn được 2 quyển sách giáo khoa”.
Vì chỉ có 1 quyển sách giáo khoa nên không thể lấy ra 2 quyển sách giáo khoa từ giá.
Do đó biến cố C là biến cố không thể.
Vậy trong các biến cố trên, biến cố B là chắc chắn; biến cố C là không thể; biến cố A là ngẫu nhiên.
Bài 2 trang 96 Toán 7 Tập 2:
Gieo hai con xúc xắc cân đối. Hãy so sánh xác suất xảy ra của các biến cố sau:
A: “Tổng số chấm xuất hiện ở mặt trên hai con xúc xắc là số chẵn”;
B: “Số chấm xuất hiện ở mặt trên hai con xúc xắc đều bằng 6”;
C: “Số chấm xuất hiện ở mặt trên hai con xúc xắc bằng nhau”.
Lời giải:
Một con xúc xắc cân đối có 6 mặt với số chấm là: 1 chấm; 2 chấm; 3 chấm; 4 chấm; 5 chấm; 6 chấm.
Kí hiệu (i; j) là kết quả con xúc xắc thứ nhất xuất hiện i chấm, con xúc xắc thứ hai xuất hiện j chấm, trong đó i, j ∈ {1; 2; 3; 4; 5; 6}.
Khi đó tập hợp tất cả các kết quả có thể xảy ra khi gieo hai con xúc xắc là:
M = {(1; 1); (1; 2); (1; 3); (1; 4); (1; 5); (1; 6); (2; 1); (2; 2); …; (6; 5); (6; 6)}.
Vậy có tất cả 6 . 6 = 36 kết quả có thể xảy ra.
• Xét biến cố A: “Tổng số chấm xuất hiện ở mặt trên hai con xúc xắc là số chẵn”.
Tổng số chấm xuất hiện ở mặt trên hai con xúc xắc là số chẵn khi số chấm xuất hiện trên hai con xúc xắc cùng chẵn hoặc cùng lẻ.
Tập hợp A các kết quả làm cho biến cố A xảy ra là:
A = {(1; 1); (1; 3); (1; 5); (2; 2); (2; 4); (2; 6); …; (6; 4); (6; 6)}.
Có tất cả 3 . 6 = 18 kết quả làm cho biến cố A xảy ra.
Do đó .
• Xét biến cố B: “Số chấm xuất hiện ở mặt trên hai con xúc xắc đều bằng 6”.
Số chấm xuất hiện ở mặt trên hai con xúc xắc đều bằng 6 khi i = 6 và j = 6.
Khi đó chỉ có 1 kết quả làm cho biến cố B xảy ra là (6; 6).
Do đó .
• Xét biến cố C: “Số chấm xuất hiện ở mặt trên hai con xúc xắc bằng nhau”.
Số chấm xuất hiện ở mặt trên hai con xúc xắc bằng nhau khi hai con xúc xắc cùng xuất hiện 1 chấm hoặc 2 chấm hoặc 3 chấm hoặc 4 chấm hoặc 5 chấm hoặc 6 chấm.
Tập hợp C các kết quả làm cho biến cố C xảy ra là:
C = {(1; 1); (2; 2); (3; 3); (4; 4); (5; 5); (6; 6)}.
Có 6 kết quả làm cho biến cố C xảy ra.
Do đó
Ta thấy nên P(A) > P(B) > P(C).
Vậy xác suất xảy ra của các biến cố B nhỏ hơn biến cố A và lớn hơn biến cố C.
Bài 3 trang 96 Toán 7 Tập 2:
Một hộp có 4 tấm thẻ có kích thước giống nhau và được đánh số lần lượt là 2, 4, 6, 8. Lấy ngẫu nhiên 1 thẻ từ hộp. Hãy tính xác suất của các biến cố sau:
A: “Lấy được thẻ ghi số nguyên tố”;
B: “Lấy được thẻ ghi số lẻ”;
C: “Lấy được thẻ ghi số chẵn”.
Lời giải:
Lấy ngẫu nhiên 1 thẻ từ hộp có 4 tấm thẻ có kích thước giống nhau và được đánh số lần lượt là 2, 4, 6, 8 nên có tất cả 4 kết quả có thể xảy ra và 4 kết quả này có cùng khả năng xảy ra.
• Xét biến cố A: “Lấy được thẻ ghi số nguyên tố”.
Trong các số 2; 4; 6; 8 chỉ có số 2 là số nguyên tố.
Do đó xác suất lấy được thẻ ghi số nguyên tố là: P(A) = .
Vậy xác suất của biến cố A bằng .
• Xét biến cố B: “Lấy được thẻ ghi số lẻ”.
Trong các số 2; 4; 6; 8 không có số nào là số lẻ.
Do đó biến cố B là biến cố không thể nên P(B) = 0.
Vậy xác suất của biến cố B bằng 0.
• Xét biến cố C: “Lấy được thẻ ghi số chẵn”.
Tất cả các số 2; 4; 6; 8 đều là các số chẵn.
Do đó biến cố C là biến cố chắc chắn nên P(C) = 1.
Vậy xác suất của biến cố C bằng 1.
Bài 4 trang 96 Toán 7 Tập 2:
Một hộp kín chứa 5 quả cầu có kích thước và khối lượng bằng nhau, trong đó có 1 quả màu xanh và 4 quả màu đỏ. Lấy ngẫu nhiên 1 quả cầu từ hộp. Hãy tính xác suất của các biến cố sau:
A: “Quả cầu lấy ra có màu vàng”;
B: “Quả cầu lấy ra có màu xanh”.
Lời giải:
Lấy ngẫu nhiên 1 quả cầu từ hộp kín chứa 5 quả cầu có kích thước và khối lượng bằng nhau nên có 5 kết quả có thể xảy ra và 5 kết quả này có cùng khả năng xảy ra.
• Xét biến cố A: “Quả cầu lấy ra có màu vàng”.
Trong 5 quả cầu, không có quả nào có màu vàng.
Do đó biến cố A là biến cố không thể nên P(A) = 0.
Vậy xác suất của biến cố A bằng 0.
• Xét biến cố B: “Quả cầu lấy ra có màu xanh”.
Trong 5 quả cầu, chỉ có 1 quả cầu màu xanh nên P(B) = .
Vậy xác suất của biến cố B bằng .
Bài 5 trang 96 Toán 7 Tập 2:
Biểu đồ dưới đây thống kê số học sinh Trung học cơ sở của tỉnh Phú Thọ trong giai đoạn từ năm 2010 đến năm 2019.
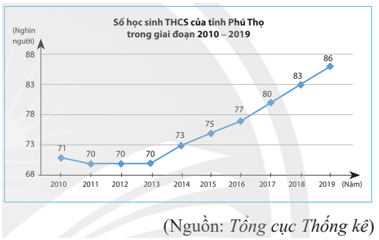
Chọn ngẫu nhiên một năm trong giai đoạn đó. Biết khả năng chọn mỗi năm là như nhau.
a) Nêu tập hợp các kết quả có thể xảy ra với năm được chọn.
b) Gọi B là biến cố “Tỉnh Phú Thọ có trên 85 000 học sinh Trung học cơ sở trong năm được chọn”. Hãy tính xác suất của biến cố B.
Lời giải:
a) Năm được chọn có thể là một trong các năm: 2010; 2011; 2012; 2013; 2014; 2015; 2016; 2017; 2018; 2019.
Vậy tập hợp các kết quả có thể xảy ra với năm được chọn là {2010; 2011; 2012; 2013; 2014; 2015; 2016; 2017; 2018; 2019}.
b) Dựa vào biểu đồ trên, trong các năm từ năm 2010 – 2019, chỉ có năm 2019 số học sinh Trung học cơ sở của tỉnh Phú Thọ có trên 85 000.
Do đó xác suất của biến cố “Tỉnh Phú Thọ có trên 85 000 học sinh Trung học cơ sở trong năm được chọn” là P(B) = .
Vậy xác suất của biến cố B là .
Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Hoạt động thực hành và trải nghiệm. Nhảy theo xúc xắc
Bài tập cuối chương 9
Bài 1: Tập hợp các số hữu tỉ
Bài 2: Các phép tính với số hữu tỉ
Bài 3: Lũy thừa của một số hữu tỉ
Đăng bởi: THCS Bình Chánh
Chuyên mục: Toán 7 Chân trời sáng tạo
- Giải Bài 9.29 trang 81 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 9.30 trang 81 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.33 trang 21 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.27 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.28 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.29 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống









