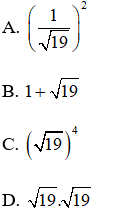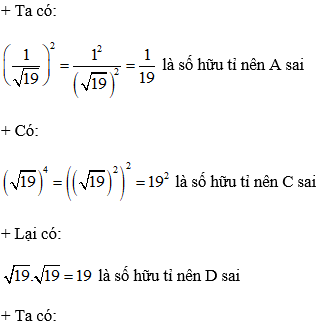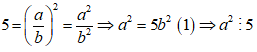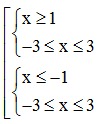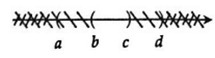I là tập hợp số gì? Bài tập vận dụng về tập hợp số

Cô Nguyễn Thanh Phương 06/06/2023

Mời các em theo dõi nội dung bài học về I là tập hợp số gì? Bài tập vận dụng về tập hợp số do thầy cô trường THCS Bình Chánh biên soạn. Hy vọng sẽ là tài liệu hữu ích giúp các em học tốt và hoàn thành tốt bài tập của mình.

Mục lục

I là tập hợp số gì?

Câu hỏi: I là tập hợp số gì?

Trả lời: Tập hợp các số vô tỉ được quy ước kí hiệu là I

Bạn đang xem: I là tập hợp số gì? Bài tập vận dụng về tập hợp số

Số hữu tỉ là gì?

Số hữu tỉ là tập hợp các số có thể viết được dưới dạng phân số (thương số). Tức là một số hữu tỉ có thể được biểu diễn bằng một số thập phân vô hạn tuần hoàn. Số hữu tỉ được viết là a/b, trong đó a và b là các số nguyên nhưng b phải khác 0

Q là tập hợp các số hữu tỉ. Vậy ta có: Q={ a/b; a, b∈Z, b≠0}

Tính chất

Tập hợp số hữu tỉ là tập hợp đếm được.
Phép nhân số hữu tỉ có dạng

$\frac{a}{b}\times\frac{c}{d}=\frac{a\times c}{b\times d}$

Phép chia số hữu tỉ có dạng

$\frac{a}{b}\div\frac{c}{d}=\frac{a\times d}{b\times c}$

Nếu số hữu tỉ là số hữu tỉ dương thì số đối của nó là số hữu tỉ âm và ngược lại. Tức tống số hữu tỉ và số đối của nó bằng 0.

Ví dụ:

Nhân số hữu tỉ:

$\frac{2}{5}\times\frac{7}{3}\times\frac{2}{3}=\frac{28}{45}$

Chia số hữu tỉ:

$\frac{4}{5}\div\frac{3}{7}=\frac{4\times7}{5\times3}=\frac{28}{15}$

Số hữu tỉ 3/2 có số đối là (-3/2). Tổng hai số đối 3/2+(-3/2) =0

Các loại số hữu tỉ phổ biến

Số hữu tỉ được phân thành 2 loại gồm số hữu tỉ âm và số hữu tỉ dương. Cụ thể:

Số hữu tỉ âm: Bao gồm những số hữu tỉ nhỏ hơn 0
Số hữu tỉ dương: Bao gồm những sổ hữu tỉ lớn hơn 0

Lưu ý: số 0 không phải là số hữu tỉ âm và cũng không phải là số hữu tỉ dương.

Công thức tính lũy thừa của 1 số hữu tỉ

Các công thức tính lũy thừa của 1 số hữu tỉ mà bạn cần phải ghi nhớ

Tích của hai lũy thừa cùng cơ số: $X^m.X^n=X^{m+n}$

Lũy thừa của lũy thừa $\left(X^m\right)^n=X^{m.n}$

Lũy thừa của một tích $\left(X.Y\right)^n=X^n.Y^n$

Lũy thừa của một thương $\left(\frac{X}{Y}\right)^n=\frac{X^n}{Y^n}$

Số vô tỉ là gì?

Khái niệm

Số vô tỉ là các số viết được dưới dạng số thập phân vô hạn không tuần hoàn.Số vô tỉ kí hiệu là I.

Các bạn cần ghi nhớ các số thực không phải là số hữu tỉ có nghĩa là các bạn không thể biểu diễn được dưới dạng tỉ số như a/ b (trong đó a, b là các số nguyên).

Tính chất

Tập hợp số vô tỉ là tập hợp không đếm được.

Ví dụ:

Số vô tỉ: 0,1010010001000010000010000001… (đây là số thập phân vô hạn không tuần hoàn)

Số căn bậc 2: √2 (căn 2)

Số pi (π): 3,14159 26535 89793 23846 26433 83279 50 288…..

Sự khác nhau giữa số hữu tỉ và số vô tỉ?

Số hữu tỉ bao gồm số thập phân vô hạn tuần hoàn, còn số vô tỉ là các số thập phân vô hạn không tuần hoàn.

Số hữu tỉ chỉ là phân số, còn số vô tỉ có rất nhiều loại số khác nhau

Số hữu tỉ là số đếm được, còn số vô tỉ là số không đếm được

Mối quan hệ các tập hợp số

Ký hiệu các tập hợp số:

N: Tập hợp số tự nhiên

N*: Tập hợp số tự nhiên khác 0

Z: Tập hợp số nguyên

Q: Tập hợp số hữu tỉ

I: Tập hợp số vô tỉ

Ta có : R = Q ∪ I.

Tập N ; Z ; Q ; R.

Khi đó quan hệ bao hàm giữa các tập hợp số là : N ⊂ Z ⊂ Q ⊂ R

Bài tập vận dụng về tập hợp số

Câu 1. Chọn đáp án sai

A. Nếu a là số nguyên thì a là số thực

B. Nếu a là số hữu tỉ thì a là số thực

C. Nếu a là số vô tỉ thì a được viết dưới dạng số thập phân vô hạn tuần hoàn

D. Nếu a là số tự nhiên thì a không phải là số vô tỉ

Lời giải:

– Số thực bao gồm cả số hữu tỉ và số vô tỉ nên B đúng

– Mọi số nguyên là số hữu tỉ nên mọi số nguyên cũng là số thực nên A đúng

– Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn nên C sai

– Số tự nhiên không viết được dưới dạng số thập phân vô hạn tuần hoàn nên D đúng

Đáp án C

Câu 2. Tìm khẳng định đúng trong các khẳng định sau đây:

A. Tích của hai số vô tỉ là số vô tỉ

B. Tổng của một số vô tỉ và một số hữu tỉ là số vô tỉ

C. Thương của hai số vô tỉ là số vô tỉ

D. Tổng của hai số vô tỉ là số vô tỉ

Lời giải:

– Tích của hai số vô tỉ chưa chắc đã là số vô tỉ

D. là số hữu tỉ

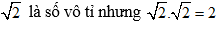
⇒ Đáp án A sai

– Tổng của một số vô tỉ và một số hữu tỉ là số vô tỉ, đúng

Thật vậy,

Giả sử khẳng định sai, khi đó tổng của một số vô tỉ và một số hữu tỉ là một số hữu tỉ.

Giả sử a là số vô tỉ (a ∈ I), b là số hữu tỉ (b ∈ Q)

Khi đó ta có: a + b = x (với x ∈ Q)

Suy ra: a = x – b

Vì x, b ∈ Q , mà hiệu của hai số hữu tỉ là một số hữu tỉ nên x – b ∈ Q mâu thuẫn với a ∈ I

Vậy giả sử sai.

Kết luận: tổng của một số vô tỉ và một số hữu tỉ là số vô tỉ.

⇒ Đáp án B đúng

– Thương của hai số vô tỉ chưa chắc đã là số vô tỉ

D. không phải là số vô tỉ

⇒ Đáp án C sai

– Tổng của hai số vô tỉ chưa chắc là số vô tỉ

D. không phải là số vô tỉ

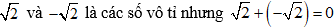
⇒ Đáp án D sai

Đáp án B

Câu 3. Chọn dấu thích hợp điền vào chỗ trống sau: 1,2345666 … R

A. ∈

B. ∉

C. ⊂

D. =

Lời giải:

1,2345666 ∈ R

Vì 1,2345666 là số thập phân hữu hạn, mà mọi số thực đều được biểu diễn dưới dạng số thập phân hữu hạn.

Đáp án A

Câu 4. Điền kí hiệu thích hợp vào chỗ trống: R ∩ Q = …

A. R

B. Q

C. ∅

D. I

Lời giải:

Ta có: R là kí hiệu của tập các số thực, Q là kí hiệu của tập các số hữu tỉ

Theo lý thuyết, R = Q ∪ I

Từ đó suy ra, R ∩ Q = Q

Đáp án B

Câu 5. Biết 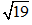là số vô tỉ. Trong các phép tính sau đây, phép tính nào có kết quả là số vô tỉ?

Lời giải:

là tổng của một số hữu tỉ với một số vô tỉ nên kết quả của là một số vô tỉ nên B đúng.

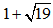
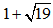
Đáp án B

Câu 6. Điền kí hiệu thích hợp vào chỗ trống: Q ∩ I = …

A. R

B. Q

C. I

D. ∅

Lời giải:

Q là tập hợp các số hữu tỉ

I là tập hợp các số vô tỉ

Do đó giao của tập số hữu tỉ và tập số vô tỉ là rỗng

Q ∩ I = ∅

Đáp án D

Câu 7. Trong các khẳng định sau, khẳng định nào sai?

A. I ⊂ R

B. Q ⊂ R

C. R ⊂ N

D. Z ⊂ R

Lời giải:

Theo lý thuyết ta có, N ⊂ Z ⊂ Q ⊂ R và R = Q ∪ I

Nên đáp án A,

B. D đúng và đáp án C sai.

Đáp án C

Câu 8. Điền kí hiệu thích hợp vào chỗ trống: 15,(3096789) ∈ ….

A. N

B. Z

C. Q

D. I

Lời giải:

Vì 15,(3096789) là số thập phân vô hạn tuần hoàn nên nó là số hữu tỉ

Vậy 15,(3096789) ∈ Q.

Đáp án C

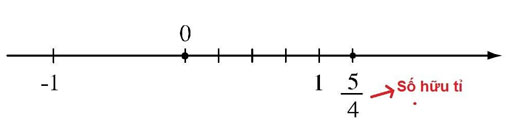
Câu 9. Số 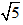là

A. Số thực

B. Số hữu tỉ

C. Số vô tỉ

D. A và C đều đúng

Lời giải:

+ Ta có: 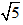là số vô tỉ

Thật vậy, giả sử 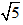là số hữu tỉ, vậy (a, b ∈ Z; b ≠ 0; (a;b) = 1)

Suy ra:

Mà 5 là số nguyên tố nên a⋮5hay a = 5k thay vào (1) ta được:

5b² = (5k)² ⇒ 5b² = 25k² ⇒ b² = 5k²

Từ đó suy ra b⋮5, mà a và b là hai số nguyên tố cùng nhau, dẫn đến mâu thuẫn

Vậy 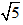là số vô tỉ.

Do đó 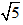là số thực.

Vậy cả A và C đều đúng.

Đáp án D

Câu 10. Thương của một số vô tỉ và một số hữu tỉ là

A. Số thực

B. Số hữu tỉ

C. Số vô tỉ

D. Cả A và C đều đúng

Lời giải:

Giả sử a là số vô tỉ và b là một số hữu tỉ khác 0.

Khi đó thương 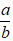là số vô tỉ

Thật vậy, giả sử 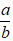= x là số hữu tỉ

Suy ra a = b.x, vì b và x là các số hữu tỉ nên tích b.x phải là số hữu tỉ (tích của hai số hữu tỉ là một số hữu tỉ), mâu thuẫn với a là số vô tỉ

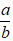
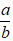
Giả sử sai, vậy là số vô tỉ, do đó là số thực.

Vậy thương của một số vô tỉ và một số hữu tỉ là một số vô tỉ và nó cũng là số thực.

Đáp án D

Câu 11: Cho tập hợp A = {x ∈ R | -3 < x < 1} . Tập A là tập nào sau đây?

A.{-3; 1}.

B. [-3; 1].

C. [-3; 1).

D. (-3; 1).

Lời giải:

Chọn D.

Theo lý thuyết: (a;b) = {x ∈ R | a < x < b}

Vậy A = {x ∈ R | -3 < x < 1} = (-3; 1).

Câu 12: Hình vẽ nào sau đây (phần không bị gạch) minh họa cho tập hợp (1; 4]?

Lời giải:

Chọn A. Vì (1; 4] gồm các số thực x mà 1 < x ≤ 4 .

Đáp án B sai vì [1; 4] gồm các số thực x mà 1 ≤ x ≤ 4 .

Đáp án C sai vì (1; 4) gồm các số thực x mà 1 < x < 4.

Đáp án B sai vì [1; 4) gồm các số thực x mà 1 ≤ x ≤ 4.

Câu 13: Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp A = { x ∈ R | 4 ≤ x ≤ 9} :

A. A = [4; 9].

B. A = (4; 9].

C. A = [4; 9).

D. A = (4; 9)

Hướng dẫn:

Chọn A.

Theo lý thuyết: [a;b] = {x ∈ R | a ≤ x ≤ b} . Suy ra A = {x ∈ R | 4 ≤ x ≤ 9} = [4; 9] .

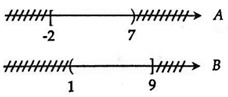
Câu 14: Cho hai tập hợp A = [-2; 7); B = (1; 9]. Tìm A ∪ B.

A. (1; 7).

B. [-2; 9].

C. [-2; 1).

D. (7; 9].

Lời giải:

Chọn B.

Ta biểu diễn tập hợp A và B trên trục số như sau:

Vậy A ∪ B = [-2;7] ∪ (1;9] = [-2;9] .

Câu 15: Cho tập hợp X = thì X được biểu diễn là hình nào sau đây?

Lời giải:

Chọn D.

Giải bất phương trình:

1 ≤ |x| ≤ 3 ⇔⇔⇔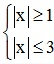

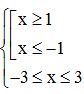
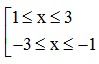
⇔ ⇔ x ∈ [-3;-1] ∪ [1;3].

Vậy đáp án D thỏa mãn x ∈ [-3;-1] ∪ [1;3] .

Câu 16: Cho hai tập hợp A = (1; 5]; B = (2; 7]. Tập hợp A \ B là:

A. (1; 2].

B. (2; 5).

C. (-1; 7].

D. (-1; 2).

Hướng dẫn:

Chọn A.

Ta biểu diễn tập hợp A và B trên trục số:

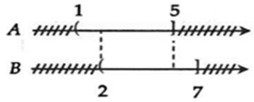
Vậy A \ B = { x ∈ R | x ∈ A và x ∉ B } ⇒ x ∈ (1; 2] .

Câu 17: Cho các số thực a, b, c, d và a < b < c < d. Khẳng định nào sau đây là đúng?

A. (a; c) ∩ (b; d) = (b; c)

B. (a; c) ∩ (b; d) = (b; c]

C. (a; c) ∩ (b; d) = [b; c)

D. (a; c) ∪ (b; d) = [b; c)

Lời giải:

Chọn A.

Ta biểu diễn (a; c); (b; d) trên trục số sau đó dựa vào tính chất giao của hai tập hợp để tìm ra đáp án:

Vậy (a; c) ∩ (b; d) = (b; c).

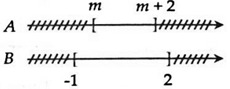
Câu 18: Cho tập hợp A = [m; m+2]; B = [-1; 2]. Tìm điều kiện của m để A ⊂ B.

A. m ≤ -1 hoặc m ≥ 0 .

B. -1 ≤ m ≤ 0 .

C. -1 ≤ m ≤ 2 .

D. m < 1 hoặc m > 2.

Lời giải:

Chọn B.

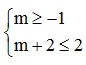
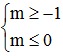
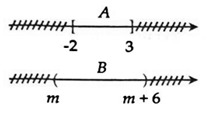
Điều kiện để A ⊂ B là: -1 ≤ m < m + 2 ≤ 2 ⇔⇔ ⇔ -1 ≤ m ≤ 0 .

Câu 19: Cho hai tập hợp A = [-2; 3]; B = (m; m+6). Điều kiện để A ⊂ B là:

A. -3 ≤ m ≤ -2

B. -3 < m < -2

C. m < -3

D. m ≥ -2

Lời giải:

Chọn B.

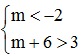
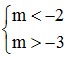
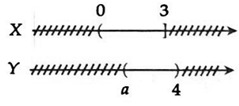
Điều kiện để A ⊂ B là m < -2 < 3 < m + 6 ⇔⇔ ⇔ -3 < m < 2 .

Câu 20: Cho hai tập hợp X = (0; 3] và Y = (a; 4). Tìm tất cả các giá trị của a ≤ 4 để X ∩ Y ≠ ∅ .

A. .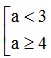

B. a < 3.

C. a < 0.

D. a > 3.

Lời giải:

Chọn B.

Xét: X ∩ Y ≠ ∅ ⇔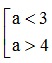⇔ 3 ≤ a ≤ 4

⇒ X ∩ Y ≠ ∅ ⇔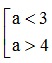. Mà theo đề bài, a ≤ 4 nên suy ra a < 3.

Vậy với a < 3 thì X ∩ Y ≠ ∅ .

***

Trên đây là nội dung bài học I là tập hợp số gì? Bài tập vận dụng về tập hợp số do thầy cô trường THCS Bình Chánh biên soạn và tổng hợp. Hy vọng sẽ giúp các em hiểu rõ nội dung bài học và từ đó hoàn thành tốt bài tập của mình. Đồng thời luôn đạt điểm cao trong các bài thi bài kiểm tra sắp tới. Chúc các em học tập thật tốt.

Đăng bởi THCS Bình Chánh trong chuyên mục Học tập