Mời các em theo dõi nội dung bài học về R là tập hợp số gì? Bài tập vận dụng về tập hập số R] do thầy cô trường THCS Bình Chánh biên soạn. Hy vọng sẽ là tài liệu hữu ích giúp các em học tốt và hoàn thành tốt bài tập của mình.
R là tập hợp số gì?
Tập hợp các số thực gồm các số thập phân hữu hạn, vô hạn tuần hoàn và vô hạn không tuần hoàn. Các số thập phân vô hạn không tuần hoàn gọi là số vô tỉ.
Tập hợp các số thực gồm các số hữu tỉ và các số vô tỉ.
Bạn đang xem: R là tập hợp số gì? Tính chất và bài tập vận dụng về tập hợp số R
Các tập hợp con thường dùng của R
Trong toán học ta thường gặp các tập hợp con sau đây của tập hợp các số thực R
Khoảng
- (a; b) = {x ∈ R| a < x < b}
- (a; +∞) = {x ∈ R| a < x}
- (–∞; b) = {x ∈ R| x < b}
Đoạn
- [a; b] = {x ∈ R| a ≤ x ≤ b}
Nửa khoảng
- [a; b) = {x ∈ R| a ≤ x < b}
- (a; b] = {x ∈ R| a < x ≤ b}
- [a; +∞) = {x ∈ R| a ≤ x}
- (–∞; b] = {x ∈ R| x ≤ b}
Tính chất của tập hợp số R và trục số thực R
- Bất kỹ một số thực nào (ngoại trừ số 0) đều có số dương và số đối nghịch với nó (số âm). Ví dụ: ta có số dương 1 thì số đối nghịch của nó là -1 (số âm).
- Tổng (kết quả phép tính cộng) hay tích (kết quả phép tính nhân) của hai số thực không âm luôn luôn là một số thực không âm.
- Đây được coi như là tính chất cơ bản và dễ nhận biết nhất của tập hợp số thực. Số thực được xem như là tập hợp vô hạn các số, với số lượng vô cùng nhiều và ta không đếm được.
- Có hệ thống các tập hợp con vô hạn có thể đếm được của các số thực
- Các phép đo đại lượng liên tục có thể được thể hiện thông qua số thực.
- Số thực có thể được biểu diễn bằng số dưới dạng số thập phân (phân số)
- Các số thực có thể được coi là các điểm trên một đường dài vô hạn được gọi là trục số, trong đó các điểm tương ứng với các số nguyên cách đều nhau. Bất kỳ số thực nào cũng có thể được xác định bằng biểu diễn thập phân vô hạn, chẳng hạn như số 8.632, trong đó mỗi chữ số liên tiếp được tính bằng một phần mười giá trị của số trước đó. Trục số thực có thể được coi là một phần của mặt phẳng phức.
R là ký hiệu của số thực trong toán học và chúng có các thuộc tính như sau:
- Các số thực bao gồm một số trường, với các phép cộng và phép nhân cùng phép chia cho các số khác 0.
- Chúng có thể được sắp xếp trên một trục hoành theo cách thương tích với phép cộng và phép nhân.
- Số thực R cho biết nếu tập hợp một số thực không trống có giới hạn trên thì nó có cận trên chính là những số thực nhỏ nhất.
- Tập hợp R cũng có thể xác định các phép toán như cộng, trừ, nhân, chia và lũy thừa. Các phép toán số thực cũng có các tính chất tương tự như các phép toán số hữu tỉ.
Biểu diễn thập phân của số thực
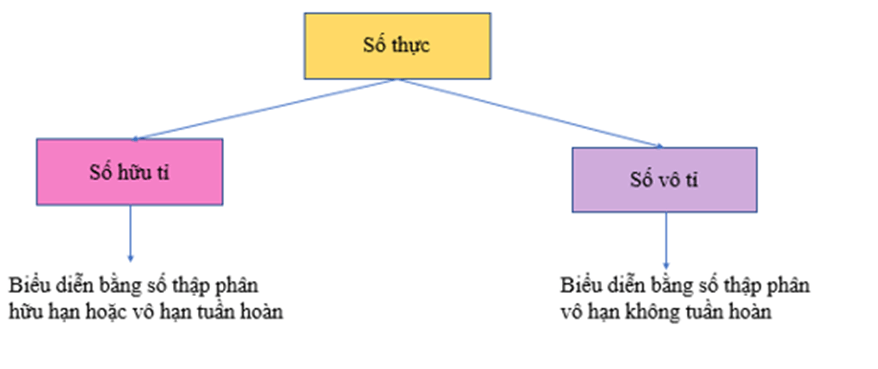
– Mỗi số thực là số hữu tỉ hoặc số vô tỉ. Vì thế, mỗi số thực đều biểu diễn được dưới dạng số thập phân hữu hạn hoặc vô hạn. Ta có sơ đồ sau:
Biểu diễn số thực trên trục số
Tương tự như số hữu tỉ, ta có thể biểu diễn mọi số thực trên trục số. Khi đó điểm biểu diễn số thực x được gọi là diểm x
Ví dụ: Biểu diễn các số thực sau trên trục số:
a) −12 và 2;
b) 2.
Hướng dẫn giải
a) Số −12 và 2 là hai số hữu tỉ, vì thế để biểu diễn hai số này trên trục số ta thực hiện như cách biểu diễn một số hữu tỉ trên trục số.
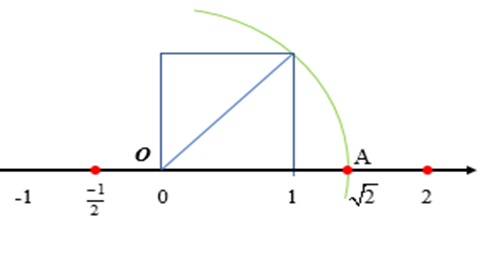
b) Số 2 là một số vô tỉ vì vậy để biểu diễn số 2 trên trục số ta làm như sau:
+ Vẽ một hình vuông với một cạnh là đoạn thẳng có hai đầu mút là điểm gốc 0 và điểm 1. Khi đó, đường chéo của hình vuông có độ dài cạnh bằng 2.
+ Vẽ một phần đường tròn tâm là điểm gốc 0, bán kính là 2, cắt trục số tại điểm A nằm bên phải gốc 0. Ta có OA = 2 và A là điểm biểu diễn 2.
Nhận xét:
– Không phải mỗi điểm trên trục số đều biểu diễn một số hữu tỉ. Vậy các điểm biểu diễn số hữu tỉ không lấp đầy trục số.
– Mỗi số thực được biểu diễn bởi một điểm trên trục số; Ngược lại, mỗi điểm trên trục số đều biểu diễn một số thực.
Vậy trục số còn được gọi là trục số thực.
Số đối của một số thực
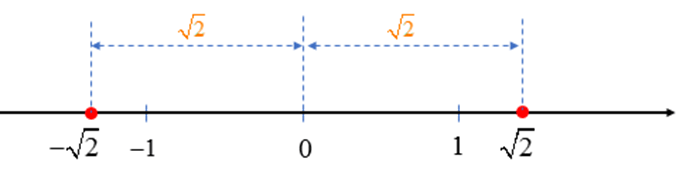
– Trên trục số, hai số thực (phân biệt) có điểm biểu diễn nằm về hai phía của điểm gốc 0 và cách đều điểm gốc 0 được gọi là hai số đối nhau.
– Số đối của số thực a kí hiệu là – a.
– Số đối của số 0 là 0.
Nhận xét: Số đối của – a là số a, tức là –(–a) = a.
Ví dụ:
Số đối của số thực 2 là số thực −2.
So sánh các số thực
So sánh hai số thực
Cũng như số hữu tỉ, trong hai số thực khác nhau luôn có một số nhỏ hơn số kia.
– Nếu số thực a nhỏ hơn số thực b thì ta biết a < b hay b > a.
– Số thực lớn hơn 0 gọi là số thực dương.
– Số thực nhỏ hơn 0 gọi là số thực âm.
– Số 0 không phải là số thực dương cũng không phải số thực âm.
– Nếu a < b và b < c thì a < c.
Cách so sánh hai số thực
– Ta có thể so sánh hai số thực bằng cách biểu diễn thập phân mỗi số thực đó rồi so sánh hai số thập phân đó.
– Việc biểu diễn một số thực dưới dạng số thập phân (hữu hạn hoặc vô hạn) thường là phức tạp. Trong một số trường hợp ta dùng quy tắc: Với a, b là hai số thực dương, nếu
a > b thì �>�.
Ví dụ: So sánh các số thực sau:
a) –1,(27) và –1,272 ;
b) 7 và 8.
Hướng dẫn giải
a) Ta viết –1,(27) = –1,27272727….. sau đó ta so sánh với –1,272.
Hai số –1,27272727… và –1,2720 có phần nguyên và đến hàng phần nghìn giống nhau, cặp chữ số khác nhau đầu tiên bắt đầu từ hàng phần chục nghìn.
Do 7 > 0 nên 1,27272727…..> 1,2720, suy ra –1,27272727…..< –1,2720.
Vậy –1,(27) < –1,272.
b) Ta có: 0 < 7 < 8 nên 7 < 8.
Minh họa trên trục số
Giả sử hai điểm x, y lần lượt biểu diễn hai số thực x, y trên trục số nằm ngang. Ta có nhận xét sau :
– Nếu x < y hay y > x thì điểm x nằm bên trái điểm y;
– Ngược lại nếu điểm x nằm bên trái điểm y thì x < y hay y > x.
Đối với hai điểm x, y lần lượt biểu diễn hai số thực x, y trên trục số thẳng đứng, ta cũng có nhận xét sau :
– Nếu x < y hay y > x thì điểm x nằm phía dưới điểm y;
– Ngược lại, nếu điểm x nằm phía dưới điểm y thì x < y hay y > x.
Ví dụ:
+ Vì −32 < –1 nên trên trục số nằm ngang, điểm −32nằm bên trái điểm –1.
+ Điểm 2 nằm bên trái điểm 5, vì vậy 2 < 5.
Các dạng câu hỏi về tập hợp số thực R
Dạng 1: Các câu hỏi về bài tập hợp số
Phương pháp sử dụng; Các ký hiệu về tập hợp số như bảng trên. Ta có quan hệ giữa các tập hợp số như sau: N ⊂ Z ⊂ Q ⊂ R; I ⊂ R. Với: N là tập hợp số tự nhiên Z là tập hợp số nguyên Q là tập hợp số hữu tỉ Z là tập hợp số vô tỉ R là tập hợp số thực
Dạng 2: tìm số chưa biết trong một đẳng thức:
Phương pháp sử dụng:
- Sử dụng các tính chất của phép toán để tính toán.
- Sử dụng mối quan hệ giữa các số hạng trong tổng và hiệu của phép tính. Cũng áp dụng như thế với các phép toán nhân chia.
- Sử dụng các quy tắc phá ngoặc và chuyển vế.
Dạng 3: Tính giá trị của biểu thức nào đó
Phương pháp sử dụng: Phối hợp giữa các phép tính nhân, chia, cộng, trừ và lũy thừa. Luôn luôn nhớ phải rút gọn phân số
Bài tập Tập hợp R các số thực
Bài 1: Tìm số đối của mỗi số sau: −56; 1,25 ; 11; −3.
Hướng dẫn giải
Số đối của số thực −56 là: −−56=56.
Số đối của số thực 1,25 là –1,25.
Số đối của 11 là −11.
Số đối của số thực −3 là −(−3)=3.
Bài 2: So sánh
a) 217 và 2,142;
b) 3 và 8.
Hướng dẫn giải
a) Ta viết 217=157=2,142857142857…. Và so sánh với số 2,1420
Ta thấy kể từ trái sang phải, cặp chữ số cùng hàng đầu tiên khác nhau là cặp chữ số ở vị trí hàng phần chục nghìn.
Do 8 > 0 nên 2,142857142857…> 2,1420. Vậy 217 > 2,142.
b) Ta có 3 > 0 và 32 = 9 nên 9=3. Để so sánh 3 và 8 ta sẽ so sánh 9 và 8.
Ta có 9 > 8 > 0 nên 9 > 8. Suy ra 3 > 8.
Trên đây là nội dung bài học R là tập hợp số gì? Tính chất và bài tập vận dụng về tập hợp số R do thầy cô trường THCS Bình Chánh biên soạn và tổng hợp. Hy vọng sẽ giúp các em hiểu rõ nội dung bài học và từ đó hoàn thành tốt bài tập của mình. Đồng thời luôn đạt điểm cao trong các bài thi bài kiểm tra sắp tới. Chúc các em học tập thật tốt.
Đăng bởi THCS Bình Chánh trong chuyện mục Học tập
- Giải Bài 9.29 trang 81 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 9.30 trang 81 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.33 trang 21 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.27 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.28 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.29 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống