Toán 10 Bài 5 Cánh diều: Phương trình đường tròn| Giải Toán lớp 10

Mời các em theo dõi nội dung bài học do thầy cô trường Trung học Bình Chánh biên soạn sẽ giúp các em nắm chắc kiến thức nội dung bài học tốt hơn.

Giải bài tập Toán 10 Bài 5: Phương trình đường tròn

A. Các câu hỏi trong bài

Bạn đang xem: Toán 10 Bài 5 Cánh diều: Phương trình đường tròn| Giải Toán lớp 10

Giải Toán 10 trang 87 Tập 2

Câu hỏi khởi động trang 87 Toán 10 Tập 2: Ở một số công viên, người ta dựng vòng quay có bán kính rất lớn đặt theo phương thẳng đứng như Hình 42. Khi vòng quay hoạt động, một người ngồi trong cabin sẽ chuyển động theo đường tròn.

Làm thế nào để xác định được phương trình quỹ đạo chuyển động của người đó?

Lời giải

Để xác định được phương trình quỹ đạo chuyển động của người đó, ta cần lập phương trình đường tròn chuyển động của vòng quay.

Hoạt động 1 trang 87 Toán 10 Tập 2:

a) Tính khoảng cách từ gốc tọa độ O(0; 0) đến điểm M(3; 4) trong mặt phẳng tọa độ Oxy.

b) Cho hai điểm I(a; b) và M(x; y) trong mặt phẳng tọa độ Oxy. Nêu công thức tính độ dài đoạn thẳng IM.

Lời giải

a) Khoảng cách từ gốc tọa độ O đến M là: $OM=\sqrt{{\left(3-0\right)}^2+{\left(4-0\right)}^2}=5$.

b) Với hai điểm I(a; b) và M(x; y) trong mặt phẳng tọa độ Oxy, ta có công thức tính độ dài đoạn thẳng IM là: $IM=\sqrt{{\left(x-a\right)}^2+{\left(y-b\right)}^2}$.

Hoạt động 2 trang 87 Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, nêu mối liên hệ giữa x và y để:

a) Điểm M(x; y) nằm trên đường tròn tâm O(0; 0) bán kính 5.

b) Điểm M(x; y) nằm trên đường tròn (C) tâm I(a; b) bán kính R.

Lời giải

a) Điểm M(x; y) nằm trên đường tròn tâm O bán kính 5 khi và chỉ khi

OM = 5

⇔ OM² = 5² 

$\iff {\left(\sqrt{{\left(x-0\right)}^2+{\left(y-0\right)}^2}\right)}^2=25$

⇔ x² + y² = 25.

b)

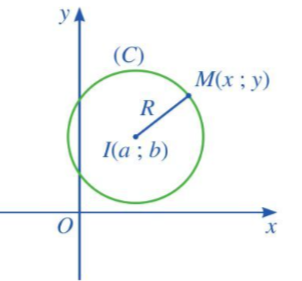
Điểm M(x; y) nằm trên đường tròn (C) tâm I(a; b) bán kính R khi và chỉ khi

IM = R

⇔ IM² = R²

$\iff {\left(\sqrt{{\left(x-a\right)}^2+{\left(y-b\right)}^2}\right)}^2=R^2$

⇔ (x – a)² + (y – b)² = R².

Giải Toán 10 trang 88 Tập 2

Luyện tập 1 trang 88 Toán 10 Tập 2: Viết phương trình đường tròn tâm I(6; – 4) đi qua điểm A(8; – 7).

Lời giải

Đường tròn tâm I đi qua điểm A nên bán kính của đường tròn là

R = IA = $\sqrt{{\left(8-6\right)}^2+{\left(\left(-7\right)-\left(-4\right)\right)}^2}=\sqrt{13}$.

Vậy phương trình đường tròn tâm I đi qua điểm A là

(x – 6)² + [y – (– 4)]² = ${\left(\sqrt{13}\right)}^2$ hay (x – 6)² + (y + 4)² = 13.

Hoạt động 3 trang 88 Toán 10 Tập 2: Viết phương trình đường tròn (C):

(x – a)² + (y – b)²  = R² về dạng x² + y² – 2ax – 2by + c = 0.

Lời giải

Ta có: (x – a)² + (y – b)²  = R²

⇔ (x² – 2ax + a²) + (y² – 2by + b²) = R² 

⇔ x² + y² – 2ax – 2by + a² + b² – R² = 0.

Đặt a² + b² – R² = c.

Vậy phương trình đường tròn (C) được đưa về dạng x² + y² – 2ax – 2by + c = 0.

Giải Toán 10 trang 89 Tập 2

Luyện tập 2 trang 89 Toán 10 Tập 2: Tìm k sao cho phương trình:

x² + y² + 2kx + 4y + 6k – 1 = 0 là phương trình đường tròn.

Lời giải

Ta có: x² + y² + 2kx + 4y + 6k – 1 = 0

⇔ (x² + 2kx + k²) + (y² + 4y + 4) – k² + 6k – 1 – 4 = 0

⇔ (x + k)² + (y + 2)² = k² – 6k + 5

Phương trình trên là phương trình đường tròn khi và chỉ khi k² – 6k + 5 > 0.

Giải bất phương trình k² – 6k + 5 > 0 ta được tập nghiệm S = (– ∞; 1) ∪ (5; + ∞).

Vậy phương trình đã cho là phương trình đường tròn khi k ∈ (– ∞; 1) ∪ (5; + ∞).

Luyện tập 3 trang 89 Toán 10 Tập 2: Lập phương trình đường tròn đi qua ba điểm A(1; 2), B(5; 2), C(1; – 3).

Lời giải

Giả sử tâm của đường tròn là điểm I(a; b).

Ta có: IA = IB = IC ⇔ IA² = IB² = IC².

Vì IA² = IB², IB² = IC² nên

$\left\{\begin{array}{l}{\left(1-a\right)}^2+{\left(2-b\right)}^2={\left(5-a\right)}^2+{\left(2-b\right)}^2\\ {\left(5-a\right)}^2+{\left(2-b\right)}^2={\left(1-a\right)}^2+{\left(-3-b\right)}^2\end{array}\right.$

$\iff \left\{\begin{array}{l}{a}^2-2a+1=a^2-10a+25\\ a^2-10a+25+b^2-4b+4=a^2-2a+1+b^2+6b+9\end{array}\right.$

$\iff \left\{\begin{array}{l}8a=24\\ 8a+10b=19\end{array}\right.$

$\iff \left\{\begin{array}{l}a=3\\ b=-\frac{1}{2}\end{array}\right.$

Đường tròn tâm I$\left(3;-\frac{1}{2}\right)$, có bán kính

R = IA = $\sqrt{{\left(1-a\right)}^2+{\left(2-b\right)}^2}$$=\sqrt{{\left(1-3\right)}^2+{\left(2-\left(-\frac{1}{2}\right)\right)}^2}=\sqrt{\frac{41}{4}}$.

Phương trình đường tròn là ${\left(x-3\right)}^2+{\left(y-\left(-\frac{1}{2}\right)\right)}^2={\left(\sqrt{\frac{41}{4}}\right)}^2$.

Vậy phương trình đường tròn là ${\left(x-3\right)}^2+{\left(y+\frac{1}{2}\right)}^2=\frac{41}{4}$.

Giải Toán 10 trang 90 Tập 2

Hoạt động 4 trang 90 Toán 10 Tập 2: Cho điểm M₀(x₀; y₀) nằm trên đường tròn (C) tâm I(a; b) bán kính R.

Gọi ∆ là tiếp tuyến tại điểm M₀(x₀; y₀) thuộc đường tròn (Hình 44).

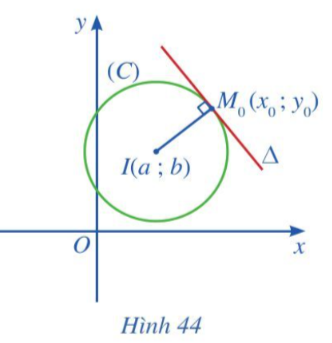
a) Chứng tỏ rằng $\overrightarrow{I{M}_0}$ là vectơ pháp tuyến của đường thẳng ∆.

b) Tính tọa độ của $\overrightarrow{I{M}_0}$.

c) Lập phương trình tổng quát của đường thẳng ∆.

Lời giải

a) Đường thẳng ∆ là tiếp tuyến của đường tròn (C) có tâm I tại điểm M₀ nên IM₀ vuông góc với ∆ tại M₀ (định nghĩa tiếp tuyến).

Vậy vectơ $\overrightarrow{I{M}_0}$ là vectơ pháp tuyến của đường thẳng ∆.

b) Ta có: $\overrightarrow{I{M}_0}=\left(x_0-a;y_0-b\right)$.

c) Đường thẳng ∆ đi qua điểm M₀(x₀; y₀) và có $\overrightarrow{I{M}_0}$ là vectơ pháp tuyến.

Vậy phương trình tổng quát của đường thẳng ∆ là(x₀ – a)(x – x₀) + (y₀ – b)(y – y₀) = 0.

Luyện tập 4 trang 90 Toán 10 Tập 2: Lập phương trình tiếp tuyến tại điểm M₀(– 1; – 4) thuộc đường tròn (x – 3)² + (y + 7)² = 25.

Lời giải

Đường tròn (x – 3)² + (y + 7)² = 25 có tâm I(3; – 7).

Phương trình tiếp tuyến tại điểm M₀(– 1; – 4) thuộc đường tròn (x – 3)² + (y + 7)² = 25 là:

(– 1 – 3)(x + 1) + (– 4 + 7)(y + 4) = 0

⇔ – 4x – 4 + 3y + 12 = 0

⇔ 4x – 3y – 8 = 0.

Vậy phương trình tiếp tuyến cần lập là 4x – 3y – 8 = 0.

B. Bài tập

Giải Toán 10 trang 91 Tập 2

Bài 1 trang 91 Toán 10 Tập 2: Phương trình nào sau đây là phương trình đường tròn?

a) x² + y² – 2x + 2y – 7 = 0;

b) x² + y² – 8x + 2y + 20 = 0.

Lời giải

a) Ta có:  x² + y² – 2x + 2y – 7 = 0

⇔ (x² – 2x + 1) + (y² + 2y + 1) – 1 – 1 – 7 = 0

⇔ (x – 1)² + (y + 1)² = 9

Phương trình trên là phương trình đường tròn với tâm I(1; – 1) và bán kính R = $\sqrt{9}$ = 3.

b) x² + y² – 8x + 2y + 20 = 0

⇔ (x² – 8x + 16) + (y² + 2y + 1) – 16 – 1 + 20 = 0

⇔ (x – 4)² + (y + 1)² = – 3

Vì – 3 < 0 nên phương trình trên không phải phương trình đường tròn.

Bài 2 trang 91 Toán 10 Tập 2: Tìm tâm và bán kính của đường tròn trong mỗi trường hợp sau:

a) Đường tròn có phương trình (x + 1)² + (y – 5)² = 9;

b) Đường tròn có phương trình x² + y² – 6x – 2y – 15 = 0.

Lời giải

a) Ta có: (x + 1)² + (y – 5)² = 9

⇔ [x – (– 1)]² + (y – 5)² = 3².

Vậy đường tròn có tâm I(– 1; 5) và bán kính R = 3.

b) Ta có: x² + y² – 6x – 2y – 15 = 0

⇔ (x² – 6x + 9) + (y² – 2y + 1) – 9 – 1 – 15 = 0

⇔ (x – 3)² + (y – 1)² = 25

⇔ (x – 3)² + (y – 1)² = 5².

Vậy đường tròn có tâm I(3; 1) và bán kính R = 5.  

Bài 3 trang 91 Toán 10 Tập 2: Lập phương trình đường tròn trong mỗi trường hợp sau:

a) Đường tròn có tâm I(– 3; 4) và bán kính R = 9;

b) Đường tròn có tâm I(5; – 2) và đi qua điểm M(4; – 1);

c) Đường tròn có tâm I(1; – 1) và có một tiếp tuyến là Δ: 5x – 12y – 1 = 0;

d) Đường tròn đường kính AB với A(3; – 4) và B(– 1; 6);

e) Đường tròn đi qua ba điểm A(1; 1); B(3; 1); C(0; 4).

Lời giải

a) Phương trình đường tròn có tâm I(– 3; 4) và bán kính R = 9 là

[x – (– 3)]² + (y – 4)² = 9² hay (x + 3)² + (y – 4)² = 81.

b) Đường tròn có tâm I và đi qua điểm M thì có bán kính là

R = IM = $\sqrt{{\left(4-5\right)}^2+{\left(\left(-1\right)-\left(-2\right)\right)}^2}=\sqrt{2}$.

Vậy phương trình đường tròn trên là

(x – 5)² + [y – (– 2)]² = ${\left(\sqrt{2}\right)}^2$ hay (x – 5)² + ( y + 2)² = 2.

c) Bán kính của đường tròn cần lập bằng khoảng cách từ tâm I của đường tròn đến tiếp tuyến ∆.

Ta có: R = d(I, ∆) = $\frac{\left|5.1-12.\left(-1\right)-1\right|}{\sqrt{5^2+{\left(-12\right)}^2}}=\frac{16}{13}$.

Vậy phương trình đường tròn là

${\left(x-1\right)}^2+{\left[y-\left(-1\right)\right]}^2={\left(\frac{16}{13}\right)}^2$ hay ${\left(x-1\right)}^2+{\left(y+1\right)}^2=\frac{256}{169}$.

d) Gọi I là trung điểm của AB, tọa độ của I là $\left\{\begin{array}{l}{x}_I=\frac{x_A+x_B}{2}=\frac{3+\left(-1\right)}{2}=1\\ y_I=\frac{y_A+y_B}{2}=\frac{\left(-4\right)+6}{2}=1\end{array}\right.$ hay I(1; 1).

Ta có: $AB=\sqrt{{\left(-1-3\right)}^2+{\left(6-\left(-4\right)\right)}^2}=2\sqrt{29}$.

Đường tròn đường kính AB có tâm là trung điểm I của AB và có bán kính R = $\frac{AB}{2}=\sqrt{29}.$

Vậy phương trình đường tròn đường kính AB là:

(x – 1)² + (y – 1)² = ${\left(\sqrt{29}\right)}^2$ hay (x – 1)² + (y – 1)² = 29.

e) Giả sử tâm của đường tròn là điểm I(a; b).

Ta có IA = IB = IC ⇔ IA² = IB² = IC².

Vì IA² = IB², IB² = IC² nên

$\left\{\begin{array}{l}{\left(1-a\right)}^2+{\left(1-b\right)}^2={\left(3-a\right)}^2+{\left(1-b\right)}^2\\ {\left(3-a\right)}^2+{\left(1-b\right)}^2={\left(0-a\right)}^2+{\left(4-b\right)}^2\end{array}\right.$

$\iff \left\{\begin{array}{l}{a}^2-2a+1=a^2-6a+9\\ a^2-6a+9+b^2-2b+1=a^2+b^2-8b+16\end{array}\right.$

$\iff \left\{\begin{array}{l}4a=8\\ -6a+6b=6\end{array}\right.\iff \left\{\begin{array}{l}a=2\\ b=3\end{array}\right.$

Đường tròn tâm I(2; 3) bán kính

R = IA = $\sqrt{{\left(1-a\right)}^2+{\left(1-b\right)}^2}$$=\sqrt{{\left(1-2\right)}^2+{\left(1-3\right)}^2}=\sqrt{5}$.

Phương trình đường tròn là ${\left(x-2\right)}^2+{\left(y-3\right)}^2={\left(\sqrt{5}\right)}^2$.

Vậy phương trình đường tròn là (x – 2)² + (y – 3)² = 5.

Giải Toán 10 trang 92 Tập 2

Bài 4 trang 92 Toán 10 Tập 2: Lập phương trình tiếp tuyến tại điểm có hoành độ bằng 3 thuộc đường tròn

(x + 2)² + (y + 7)² = 169.

Lời giải

Ta có: (x + 2)² + (y + 7)² = 169

⇔ [x – (–2)]² + (y – (–7))² = 13².

Vậy đường tròn đã cho có tâm I(– 2; – 7) và bán kính R = 13.

Vì tiếp điểm thuộc đường tròn đã cho nên tọa độ tiếp điểm thỏa mãn phương trình đường tròn.

Hoành độ của tiếp điểm là 3, tức là x = 3, thay vào phương trình đường tròn ta có:

(3 + 2)² + (y + 7)² = 169

⇔ (y + 7)² = 144

⇔ (y + 7)² = 12² 

Do đó y + 7 = 12 hoặc y + 7 = – 12

Suy ra y = 5 hoặc y = – 19.

Vậy các điểm thuộc đường tròn có hoành độ bằng 3 là A(3; 5) và B(3; – 19).

+) Phương trình tiếp tuyến của đường tròn tâm I(– 2; – 7) tại điểm A(3; 5) là

(3 + 2)(x – 3) + (5 + 7)(y – 5) = 0

⇔ 5x – 15 + 12y – 60 = 0

⇔ 5x + 12y – 75 = 0.

+) Phương trình tiếp tuyến của đường tròn tâm I(– 2; – 7) tại B(3; – 19) là

(3 + 2)(x – 3) + (– 19 + 7)[y – (– 19)] = 0

⇔ 5x – 15 – 12y – 228 = 0

⇔ 5x – 12y – 243 = 0.

Vậy các phương trình tiếp tuyến thỏa mãn yêu cầu bài toán là 5x + 12y – 75 = 0; 5x – 12y – 243 = 0.

Bài 5 trang 92 Toán 10 Tập 2: Tìm m sao cho đường thẳng 3x + 4y + m = 0 tiếp xúc với đường tròn

(x + 1)² + (y – 2)² = 4.

Lời giải

Ta có: (x + 1)² + (y – 2)² = 4

⇔ [x – (– 1)]² + (y – 2)² = 2².

Đường tròn đã cho có tâm I(– 1; 2) và bán kính R = 2.

Giả sử ∆: 3x + 4y + m = 0.

Ta có ∆ tiếp xúc với đường tròn đã cho khi và chỉ khi khoảng cách từ tâm I của đường tròn đến đường thẳng ∆ bằng bán kính của đường tròn, có nghĩa là

d(I, ∆) = R

$\iff \frac{\left|3.\left(-1\right)+4.2+m\right|}{\sqrt{3^2+4^2}}=2$

$\iff \frac{\left|m+5\right|}{5}=2$ 

⇔ |m + 5| = 10

Suy ra m + 5 = 10 hoặc m + 5 = – 10

Do đó, m = 5 hoặc m = – 15.

Vậy m = 5, m = – 15 thì thỏa mãn yêu cầu bài toán.

Bài 6 trang 92 Toán 10 Tập 2: Hình 46 mô phỏng một trạm thu phát sóng điện thoại di động đặt ở vị trí I có toạ độ (– 2; 1) trong mặt phẳng toạ độ (đơn vị trên hai trục là ki-lô-mét).

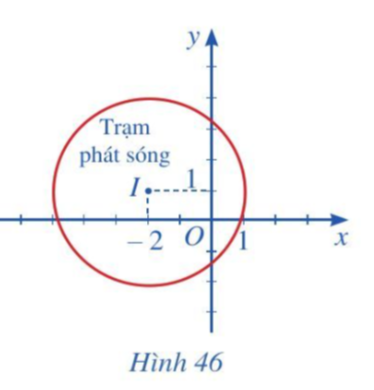
a) Lập phương trình đường tròn mô tả ranh giới bên ngoài của vùng phủ sóng, biết rằng trạm thu phát sóng đó được thiết kế với bán kính phủ sóng 3 km.

b) Nếu người dùng điện thoại ở vị trí có toạ độ (– 1; 3) thì có thể sử dụng dịch vụ của trạm này không? Giải thích.

c) Tính theo đường chim bay, xác định khoảng cách ngắn nhất để một người ở vị trí có toạ độ (– 3; 4) di chuyển được tới vùng phủ sóng theo đơn vị ki-lô-mét (làm tròn kết quả đến hàng phần mười).

Lời giải

a) Đường tròn mô tả ranh giới bên ngoài của vùng phủ sóng có tâm I(– 2; 1) và bán kính R = 3.

Vậy phương trình đường tròn là

[x – (– 2)]² + (y – 1)² = 3² hay (x + 2)² + (y – 1)² = 9.

b) Gọi M(– 1; 3) là vị trí của người dùng điện thoại.

Khoảng cách từ tâm I của đường tròn mô tả ranh giới bên ngoài của vùng phủ sóng tới vị trí M(– 1; 3) là

IM = $\sqrt{{\left(\left(-1\right)-\left(-2\right)\right)}^2+{\left(3-1\right)}^2}=\sqrt{5}$.

Mà $\sqrt{5}<3$ nên IM < R.

Khi đó vị trí M(– 1; 3) nằm trong đường tròn mô tả ranh giới bên ngoài của vùng phủ sóng.

Vậy người dùng điện thoại ở vị trí có tọa độ (– 1; 3) có thể sử dụng dịch vụ của trạm thu  phát sóng này.

c) Gọi vị trí người đó đang đứng là A(– 3; 4).

Ta có: $\overrightarrow{AI}=\left(-2-\left(-3\right);1-4\right)$, do đó $\overrightarrow{AI}=\left(1;-3\right)$.

Suy ra $AI=\sqrt{1^2+{\left(-3\right)}^2}=\sqrt{10}$ > 3 = R.

Vì AI > R nên A nằm ngoài đường tròn ranh giới.

Giả sử đường thẳng AI cắt đường tròn tại điểm B.

Do đó, AB là khoảng cách từ A đến vùng phủ sóng.

Đường thẳng AI có vectơ $\overrightarrow{AI}=\left(1;-3\right)$ vectơ chỉ phương.

Suy ra AI có vectơ pháp tuyến là $\overrightarrow{n}=\left(3;1\right)$.

Vậy phương trình đường thẳng AI là

3(x + 3) + 1(y – 4) = 0 hay 3x + y + 5 = 0.

Vì B là giao điểm của AI và đường tròn mô tả ranh giới nên tọa độ của điểm B là nghiệm của hệ phương trình $\left\{\begin{array}{l}3x+y+5=0\\ {\left(x+2\right)}^2+{\left(y–1\right)}^2=9\end{array}\right.$.

Giải hệ phương trình ta có:

$\left\{\begin{array}{l}3x+y+5=0\\ {\left(x+2\right)}^2+{\left(y–1\right)}^2=9\end{array}\right.$

$\iff \left\{\begin{array}{l}y=-3x-5\\ {\left(x+2\right)}^2+{\left(-3x-5-1\right)}^2=9\end{array}\right.$

$\iff \left\{\begin{array}{l}y=-3x-5\\ x^2+4x+4+9x^2+36x+36=9\end{array}\right.$ 

$\iff \left\{\begin{array}{l}y=-3x-5\\ 10x^2+40x+31=0\end{array}\right.$

$\iff \left\{\begin{array}{l}y=-3x-5\\ \left[\begin{array}{l}x=\frac{-20+3\sqrt{10}}{10}\\ x=\frac{-20-3\sqrt{10}}{10}\end{array}\right.\end{array}\right.$

$\iff \left[\begin{array}{l}\left\{\begin{array}{l}x=\frac{-20+3\sqrt{10}}{10}\\ y=\frac{10-9\sqrt{10}}{10}\end{array}\right.\\ \left\{\begin{array}{l}x=\frac{-20-3\sqrt{10}}{10}\\ y=\frac{10+9\sqrt{10}}{10}\end{array}\right.\end{array}\right.\iff \left[\begin{array}{l}B\left(\frac{-20+3\sqrt{10}}{10};\frac{10-9\sqrt{10}}{10}\right)\\ B\left(\frac{-20-3\sqrt{10}}{10};\frac{10+9\sqrt{10}}{10}\right)\end{array}\right.$

+ Với $B\left(\frac{-20+3\sqrt{10}}{10};\frac{10-9\sqrt{10}}{10}\right)$

Ta có: $AB=\sqrt{{\left(\frac{-20+3\sqrt{10}}{10}-\left(-3\right)\right)}^2+{\left(\frac{10-9\sqrt{10}}{10}-4\right)}^2}\approx \mathrm{6,2}$

+ Với $B\left(\frac{-20-3\sqrt{10}}{10};\frac{10+9\sqrt{10}}{10}\right)$

Ta có: $AB=\sqrt{{\left(\frac{-20-3\sqrt{10}}{10}-\left(-3\right)\right)}^2+{\left(\frac{10+9\sqrt{10}}{10}-4\right)}^2}\approx \mathrm{0,2}$

Vì 0,2 < 6,2 mà khoảng cách cần xác định là ngắn nhất nên AB ≈ 0,2.

Vậy tính theo đường chim bay, khoảng cách ngắn nhất để một người ở vị trí có toạ độ (– 3; 4) di chuyển được tới vùng phủ sóng khoảng 0,2 km.

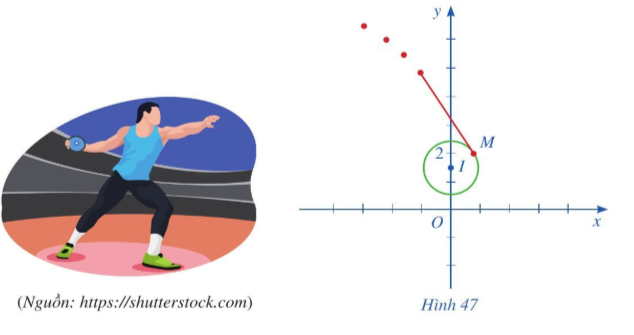
Bài 7 trang 92 Toán 10 Tập 2: Ném đĩa là một môn thể thao thi đấu trong Thế vận hội Olympic mùa hè. Khi thực hiện cú ném, vận động viên thường quay lưng lại với hướng ném, sau đó xoay ngược chiều kim đồng hồ một vòng rưỡi của đường tròn để lấy đà rồi thả tay ra khỏi đĩa. Giả sử đĩa chuyển động trên một đường tròn tâm $I\left(0;\frac{3}{2}\right)$ bán kính 0,8 trong mặt phẳng tọa độ Oxy (đơn vị trên hai trục là mét). Đến điểm $M\left(\frac{\sqrt{39}}{10};2\right)$, đĩa được ném đi (Hình 47). Trong những giây đầu tiên ngay sau khi được ném đi, quỹ đạo chuyển động của chiếc đĩa có phương trình như thế nào?

Lời giải

Đĩa chuyển động trên một đường tròn tâm $I\left(0;\frac{3}{2}\right)$ bán kính 0,8, đến điểm $M\left(\frac{\sqrt{39}}{10};2\right)$, đĩa được ném đi.

Khi đó trong những giây đầu tiên sau khi ném đi, đĩa chuyển động trên một đường thẳng chính là tiếp tuyến của đường tròn tâm I, bán kính 0,8 tại tiếp điểm M.

Phương trình tiếp tuyến của đường tròn tâm $I\left(0;\frac{3}{2}\right)$ tại tiếp điểm $M\left(\frac{\sqrt{39}}{10};2\right)$ là

$\left(\frac{\sqrt{39}}{10}-0\right)\left(x-\frac{\sqrt{39}}{10}\right)+\left(2-\frac{3}{2}\right)\left(y-2\right)=0$

$\iff \frac{\sqrt{39}}{10}x-\frac{39}{100}+\frac{1}{2}y-1=0$

$\iff 10\sqrt{39}x+50y-139=0$.

Vậy trong những giây đầu tiên ngay sau khi được ném đi, quỹ đạo chuyển động của chiếc đĩa có phương trình là $10\sqrt{39}x+50y-139=0$.

Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác: 

Bài 6: Ba đường conic

Bài tập cuối chương 7

Chủ đề 2: Xây dựng mô hình hàm số bậc nhất, bậc hai biểu diễn số liệu dạng bảng

Bài 1: Mệnh đề toán học

Bài 2: Tập hợp. Các phép toán trên tập hợp

Đăng bởi: THCS Bình Chánh

Chuyên mục: Toán 10 Cánh Diều

• Giải Bài 4.16 trang 65 Toán 10 tập 1 SGK Kết nối tri thức với cuộc sống
• Giải Bài 1 trang 37 Toán 10 tập 1 SGK Chân trời sáng tạo
• Giải Vận dụng trang 30 Toán 10 tập 1 SGK Kết nối tri thức với cuộc sống
• Triều cường là gì? Triều cường xảy ra khi nào?
• Thơ Đường luật là gì? Đặc điểm của thơ Đường luật
• Phân tích nhân vật he ra clet hay nhất (5 mẫu)