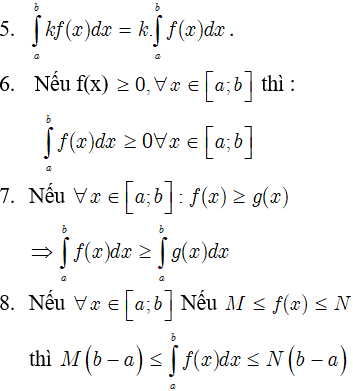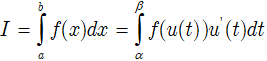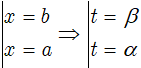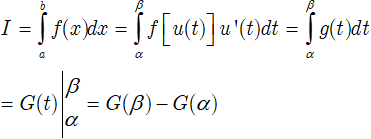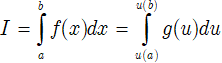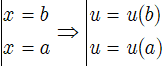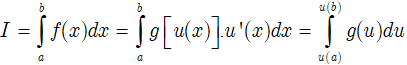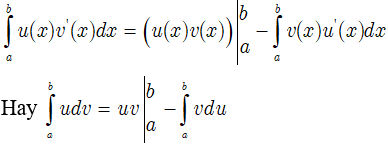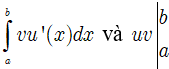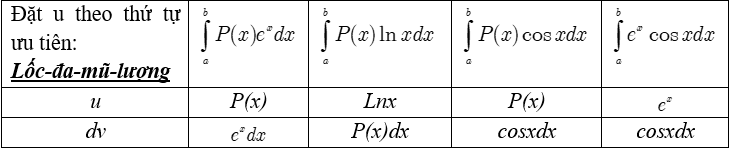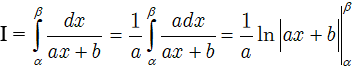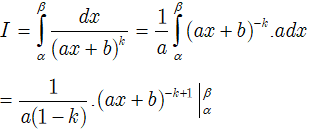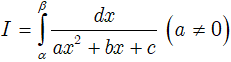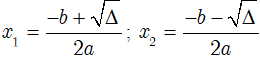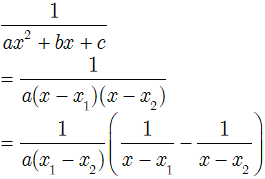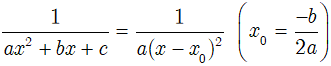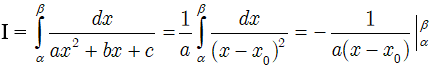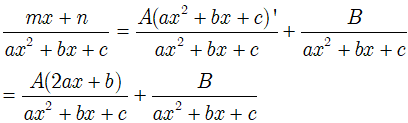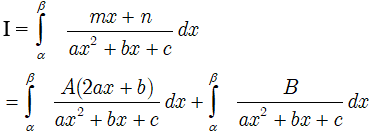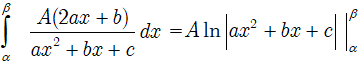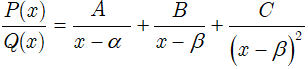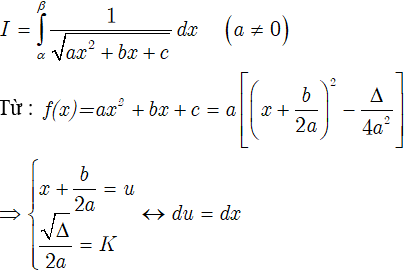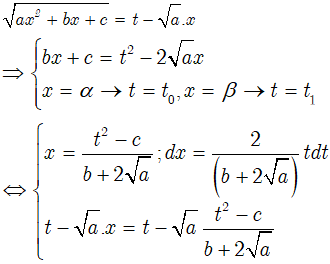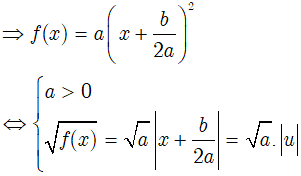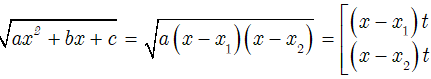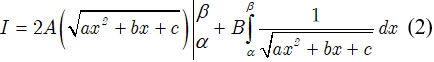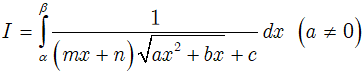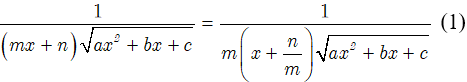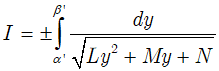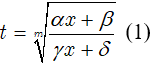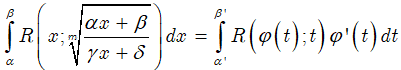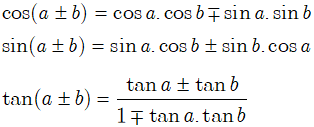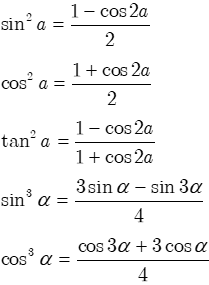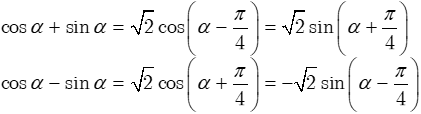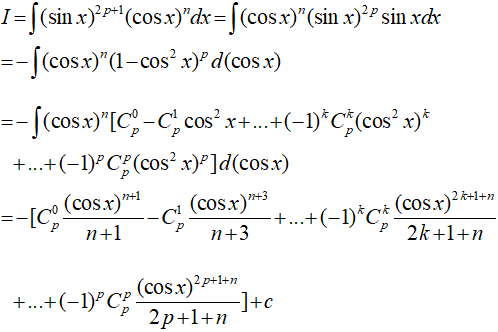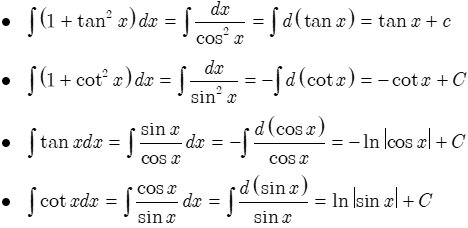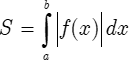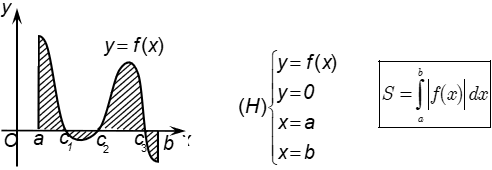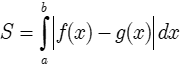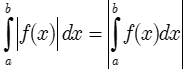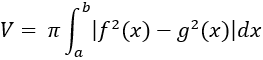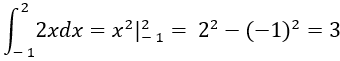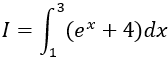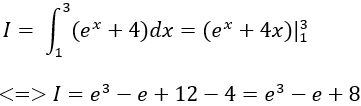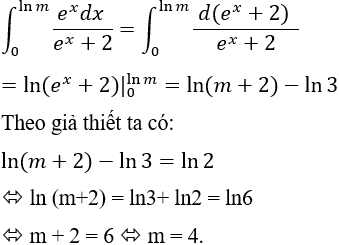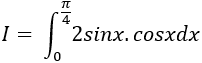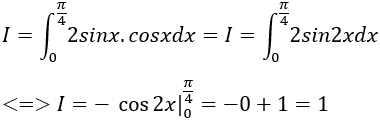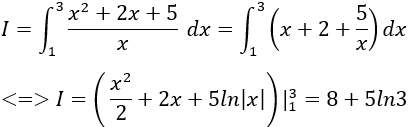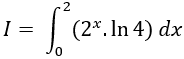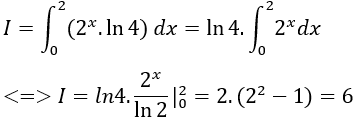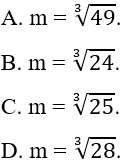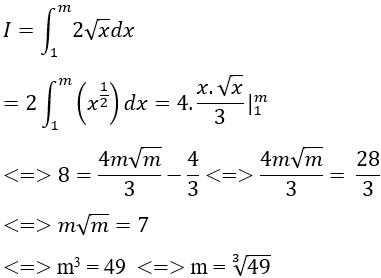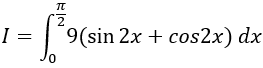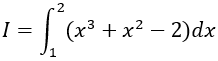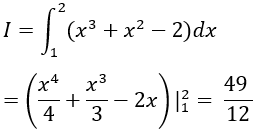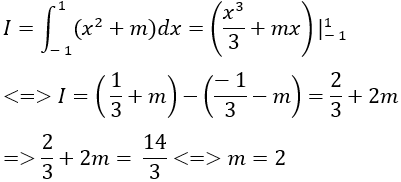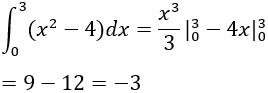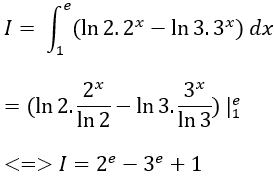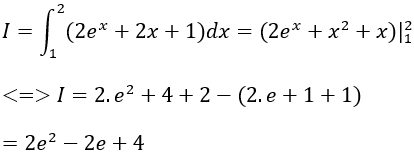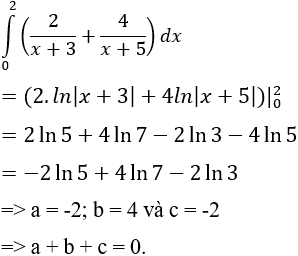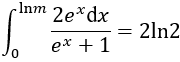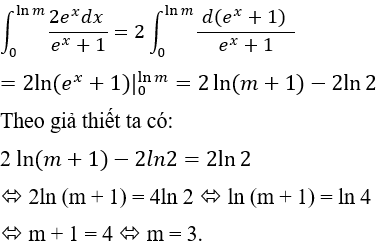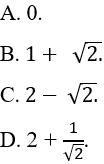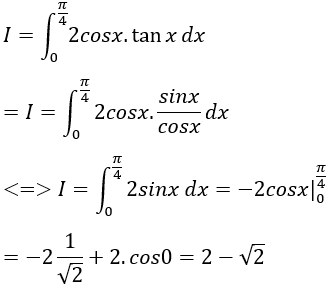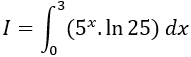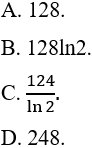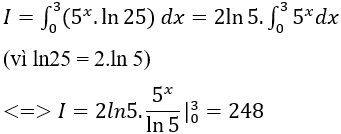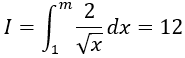Mời các em theo dõi nội dung bài học về Công thức tích phân và bài tập vận dụng do thầy cô trường THCS Bình Chánh biên soạn. Hy vọng sẽ là tài liệu hữu ích giúp các em học tốt và hoàn thành tốt bài tập của mình.
Công thức tích phân
Khái niệm tích phân
* Định nghĩa:
Cho hàm số f liên tục trên K và a, b là hai số bất kì thuộc K. Nếu F là một nguyên hàm của f trên K thì hiệu số:
Bạn đang xem: Công thức tích phân và bài tập vận dụng
F(b) – F(a)
Được gọi là tích phân của f từ a đến b và kí hiệu:
* Nhận xét: Tích phân của hàm số f từ a đến b có thể kí hiệu bởi
Tích phân đó chỉ phụ thuộc vào f và các cận a; b mà không phụ thuộc vào cách ghi biến số.
* Định lí: Cho hàm số y = f(x) liên tục; không âm trên đoạn [a;b]. Khi đó, diện tích S của hình thang cong giới hạn bởi đồ thị hàm số y = f(x); trục hoành và hai đường thẳng x = a; x = b là:
Tính chất của tích phân
Giả sử cho hai hàm số f(x) và g(x) liên tục trên K và a, b, c là ba số bất kỳ thuộc K. Khi đó ta có :
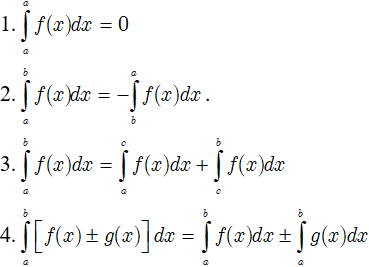
Một số phương pháp tính tích phân
1. Phương pháp đổi biến số
1.1. Phương pháp đổi biến số dạng 1
Định lí
Nếu:
1) Hàm x = u(t) có đạo hàm liên tục trên [α;β].
2) Hàm hợp f [u(t)] được xác định trên [α;β].
3) u(α) = a; u(β) = b.
Khi đó:
Phương pháp chung
• Bước 1: Đặt x = u(t).
• Bước 2: Tính vi phân hai vế: x = u(t) ⇒ dx = u'(t)dt.
Đổi cận:
• Bước 3: Chuyển tích phân đã cho sang tích phân theo biến t.
Vậy:
1.2. Phương pháp đổi biến dạng 2
Định lí
Nếu hàm số u = u(x) đơn điệu và có đạo hàm liên tục trên đoạn [a;b] sao cho f(x)dx = g(u(x))u'(x)dx = g(u)du thì:
Phương pháp chung
• Bước 1: Đặt u = u(x) ⇒ du = u’(x)dx
• Bước 2: Đổi cận:
• Bước 3: Chuyển tích phân đã cho sang tích phân theo u.
Vậy:
2. Phương pháp tích phân từng phần
a. Định lí
Nếu u(x) và v(x) là các hàm số có đạo hàm liên tục trên [a;b] thì:
b. Phương pháp chung
• Bước 1: Viết f(x)dx dưới dạng udv = u.v’dx bằng cách chọn một phần thích hợp của f(x) làm u(x) và phần còn lại dv = v'(x)dx
• Bước 2: Tính du = u’dx và v = ∫dv = ∫v'(x)dx
• Bước 3: Tính
* Cách đặt u và dv trong phương pháp tích phân từng phần.
3. Tích phân các hàm số sơ cấp cơ bản
3.1. Tích phân hàm hữu tỉ
Dạng 1
(với a ≠ 0)
Chú ý: Nếu
Dạng 2
(ax2 + bx + c ≠ 0 với mọi x ∈ [α;β])
Xét Δ = b2 – 4ac.
• Nếu Δ > 0 thì
thì:
• Nếu Δ = 0 thì:
thì:
• Nếu Δ < 0 thì:
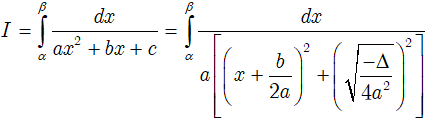
Dạng 3
(trong đó liên tục trên đoạn [α;β])
• Bằng phương pháp đồng nhất hệ số, ta tìm A và B sao cho:
• Ta có:
Tích phân:
Tích phân: 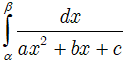
Dạng 4

• Nếu bậc của P(x) lớn hơn hoặc bằng bậc của Q(x) thì dùng phép chia đa thức.
• Nếu bậc của P(x) nhỏ hơn bậc của Q(x) thì có thể xét các trường hợp:
• Khi Q(x) chỉ có nghiệm đơn α1, α2, α3 … thì đặt
• Khi Q(x) có nghiệm đơn và vô nghiệm:
Q(x) = (x – α)(x2 + px + q), Δ = p2 – 4q < 0 thì đặt:
• Khi Q(x) có nghiệm bội:
Q(x) = (x – α)(x – β)2 với α ≠ β thì đặt:
Q(x) = (x – α)2(x – β)3 với α ≠ β thì đặt:
3.2. Tích phân hàm vô tỉ
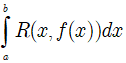
Dạng 1
Khi đó ta có:
• Nếu Δ < 0, a > 0 ⇒ f(x) = a(u2 + k2)
• Nếu: Δ = 0
• Nếu: Δ > 0
Với a > 0: f(x) = a(x – x1)(x – x2)
Với a < 0: f(x) = -a(x1 – x)(x2 – x)
Căn cứ vào phân tích trên, ta có một số cách giải sau:
Phương pháp:
* Trường hợp: Δ < 0, a > 0 ⇒ f(x) = a(u2 + k2)
Khi đó đặt:
* Trường hợp: Δ = 0
Khi đó:
* Trường hợp: Δ > 0, a > 0. Đặt:
* Trường hợp: Δ > 0, a < 0. Đặt:
Dạng 2
Phương pháp:
• Bước 1:
Phân tích:
• Bước 2:
Quy đồng mẫu số, sau đó đồng nhất hệ số hai tử số để suy ra hệ hai ẩn số A, B
• Bước 3:
Giải hệ tìm A, B thay vào (1)
• Bước 4:
Tính:
Trong đó 
Dạng 3
Phương pháp:
• Bước 1:
Phân tích:
• Bước 2:
• Bước 3:
Thay tất cả vào (1) thì I có dạng:
Tích phân này chúng ta đã biết cách tính.
Dạng 4
(Trong đó: R(x,y) là hàm số hữu tỷ đối với hai biến số x, y và α, β, γ, δ là các hằng số đã biết)
Phương pháp:
• Bước 1:
Đặt:
• Bước 2:
Tính x theo t: Bằng cách nâng lũy thừa bậc m hai vế của (1) ta có dạng x = φ(t).
• Bước 3:
Tính vi phân hai vế: dx = φ'(t)dt và đổi cận.
• Bước 4:
Tính:
3.3. Tích phân hàm lượng giác
3.3.1. Một số công thức lượng giác
* Công thức cộng
* Công thức nhân đôi
* Công thức hạ bậc
* Công thức tính theo t
* Công thức biến đổi tích thành tổng
* Công thức biến đổi tổng thành tích
* Công thức thường dùng:
Hệ quả:
3.3.2. Một số dạng tích phân lượng giác
• Nếu gặp dạng 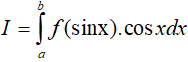
• Nếu gặp dạng 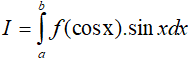
• Nếu gặp dạng 
• Nếu gặp dạng 
Dạng 1
I1 = ∫(sinx)n dx; I2 = ∫(cosx)n dx
* Phương pháp
• Nếu n chẵn thì sử dụng công thức hạ bậc.
• Nếu n = 3 thì sử dụng công thức hạ bậc hoặc biến đổi.
• Nếu n lẻ (n = 2p + 1) thì thực hiện biến đổi:

Dạng 2
I = ∫sinmx.cosnx dx (m, n ∈ N)
* Phương pháp
• Trường hợp 1: m, n là các số nguyên
a. Nếu m chẵn, n chẵn thì sử dụng công thức hạ bậc, biến đổi tích thành tổng.
b. Nếu m chẵn, n lẻ (n = 2p + 1) thì biến đổi:
c. Nếu m lẻ (m = 2p + 1), n chẵn thì biến đổi:
Dạng 3
I1 = ∫(tanx)n dx; I2 = ∫(cotx)n dx (n ∈ N)

Ứng dụng tích phân
1. Diện tích hình phẳng
a. Diện tích hình phẳng giới hạn bởi 1 đường cong và trục hoành
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) liên tục trên đoạn [a;b], trục hoành và hai đường thẳng x = a; x = b được xác định:
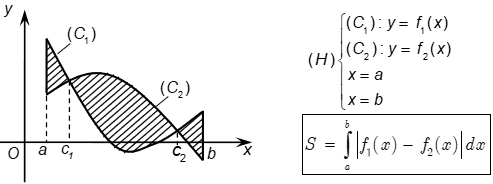
b. Diện tích hình phẳng giới hạn bởi 2 đường cong
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x); y = g(x) liên tục trên đoạn [a;b] và hai đường thẳng x = a; x = b được xác định:
– Nếu trên đoạn [a;b], hàm số f(x) không đổi dấu thì:
– Nắm vững cách tính tích phân của hàm số có chứa giá trị tuyệt đối.
– Diện tích của hình phẳng giới hạn bởi các đường x = g(y),x = h(y) và hai đường thẳng y = c; y = d được xác định:
2. Thể tích vật thể và thể tích khối tròn xoay
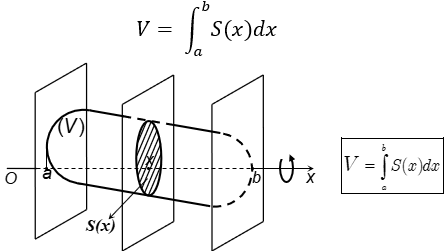
a. Thể tích vật thể
Gọi B là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a và b; S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm a (a ≤ x ≤ b). Giả sử S(x) là hàm số liên tục trên đoạn [a;b]. Thể tích của B là:
b. Thể tích khối tròn xoay
Cho hàm số y = f(x) liên tục; không âm trên [a;b]. Hình phẳng giới hạn bởi đồ thị hàm số y = f(x); trục hoành và hai đường thẳng x = a; x = b quay quanh trục Ox tạo nên một khối tròn xoay. Thể tích của nó là:
– Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường x = g(y), trục tung và hai đường thẳng y = c; y = d quay quanh trục Oy là:
– Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y = f(x); y = g(x) và hai đường thẳng x = a; x = b quay quanh trục Ox:
Ví dụ minh họa
Ví dụ 1. Tính 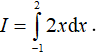
A. 6.
B. -3.
C. 3.
D. –6.
Lời giải
Ta có:
Chọn C.
Ví dụ 2. Tính
A. e3 – e + 8.
B. e3 + e – 3.
C. e3 – e + 6.
D. e3 + 2e + 8.
Lời giải
Ta có:
Chọn A.
Ví dụ 3. Cho 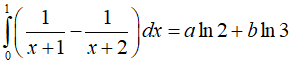
A. a + b = 0.
B. a – 2b = 0.
C. a – b = -1.
D. a + 2b = 0.
Lời giải
Ta có:
Chọn D.
Ví dụ 4. Cho 
A. m = 1.
B. m = 2.
C. m = 4.
D. m = 0.
Lời giải
Điều kiện: m > 0.
Ta có:
Chọn C.
Ví dụ 5. Tính
A. 0.
B. -1.
C. 1.
D. 2.
Lời giải
Ta có:
Chọn C.
Ví dụ 6. Tính
A. 8 + 5ln3.
B. 6 – 5ln3.
C. 12 + 3ln5.
D. 11.
Lời giải
Ta có:
Chọn A.
Ví dụ 7. Tính
A. 4. B. 4ln2. C. 4/ln2. D. 6.
Lời giải
Ta có:
Chọn D.
Ví dụ 8. Cho 
Lời giải
Ta có:
Chọn A.
Ví dụ 9. Tính
A. 0.
B. 9.
C. 18.
D. -9.
Lời giải
Ta có:
Chọn B.
Ví dụ 10. Tính
Lời giải
Ta có:
Chọn D.
Ví dụ 11. Cho 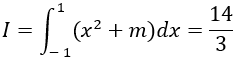
A. m = 0. B. m = -1. C. m = 1. D. m = 2.
Lời giải
Ta có:
Chọn D.

Bài tập vận dụng
Câu 1: Tính
Chọn kết quả đúng:
A. 6.
B. -3.
C. 3.
D. –6.
Ta có:
Chọn B.
Câu 2: Tính
A. ln2.2e – ln3.3e.
B. ln2.2e – ln3.3e + 1.
C. 2e – 3e.
D. 2e – 3e + 1.
Ta có:
Chọn D.
Câu 3: Tính
A. 2e2 – 2e + 4.
B. 2e3 + 2e + 2.
C. 2e2 – 2e + 8.
D. 2e2 + 2e + 8.
Ta có:
Chọn A.
Câu 4: Cho
với a; b;c là các số nguyên. Mệnh đề nào dưới đây đúng?
A. a + b + c = 0.
B. a – 2b + c = 0.
C. a – b + c = -1.
D. a + 2b = 0.
Ta có:
Chọn A.
Câu 5: Cho
Khi đó giá trị của m là:
A. m = 1.
B. m = 3.
C. m = 4.
D. m = 0.
Điều kiện m > 0.
Ta có:
Chọn B.
Câu 6: Tính
Ta có:
Chọn C.
Câu 7: Tính
Ta có:
Chọn A.
Câu 8: Tính
Ta có:
Chọn D.
Câu 9: Cho
Tìm m?
A. m = 20.
B. m = 16.
C. m = 4.
D. m = 8.
Ta có:
Chọn B.
Câu 10: Tính
A. 0.
B. -2.
C. 4.
D. -3.
Ta có:
Chọn B.
Câu 11: Tính
Ta có:
Chọn D.
Trên đây là nội dung bài học Công thức tích phân và bài tập vận dụng do thầy cô trường THCS Bình Chánh biên soạn và tổng hợp. Hy vọng sẽ giúp các em hiểu rõ nội dung bài học và từ đó hoàn thành tốt bài tập của mình. Đồng thời luôn đạt điểm cao trong các bài thi bài kiểm tra sắp tới. Chúc các em học tập thật tốt.
Đăng bởi THCS Bình Chánh trong chuyên mục Học tập
- Cảm nhận của anh (chị) về vùng đất và con người miền cực nam của Tổ quốc qua truyện ngắn Bắt sấu rừng U Minh Hạ lớp 12 (9 Mẫu)
- Anh (chị) hãy bày tỏ quan điểm của mình về ý kiến của nhà văn Pháp La Bơ-ruy-e: “Khi một tác phẩm nâng cao tinh thần ta lên và gợi cho ta những tình cảm cao quý và can đảm, không cần tìm một nguyên tắc nào để đánh giá nó nữa: đó là một cuốn sách hay và do một nghệ sĩ viết ra” lớp 12 (10 Mẫu)
- Buy-phông, nhà văn Pháp nổi tiếng, có viết: “Phong cách chính là người”. Anh (chị) hiểu ý kiến trên như thế nào? lớp 12 (12 Mẫu)
- Một trong những bức thư luận bàn về văn chương, Nguyễn Văn Siêu có viết: “Văn chương […] có loại đáng thờ, có loại không đáng thờ. Loại không đáng thờ là loại chỉ chuyên chú ở văn chương. Loại đáng thờ là loại chuyên chú ở con người. Anh chị hãy phát biểu ý kiến của mình về quan niệm trên lớp 12 (7 Mẫu)
- Viết bài văn trong đó vận dụng tổng hợp ít nhất ba thao tác lập luận, theo chủ đề: một tác phẩm văn học mới ra đời và đáng được nhiều người quan tâm bàn luận lớp 12
- Viết bài văn nghị luận trong đó vận dụng tổng hợp ít nhất ba thao tác lập luận khác nhau lớp 12 (3 Mẫu)
- “Mỗi người sinh ra đều là thiên tai” (An-be Anh-xtanh). Em hiểu câu nói này như thế nào? Hãy trình bày cách hiểu của mình cho các bạn cùng nghe (13 mẫu)
- “Cười là một hình thức chế ngự cái xấu” (Phương Lựu – Trần Đình Sử – Lê Ngọc Trà, Lí luận văn học, tập 1, NXB Giáo dục, 1986, tr. 241). Viết đoạn văn (khoảng 7 – 9 câu) trình bày suy nghĩ của em về ý kiến trên lớp 8 (6 Mẫu)
- 1 hải lý bằng bao nhiêu km? Một số quy đổi hải lý thường dùng
- 1 Lunatic 1 Ice Pick là gì? Video gây án khiến cả thế giới phải rúng động
- 10 mẫu mở bài Từ ấy hay nhất
- 100+ Ca dao tục ngữ về thầy cô hay và ý nghĩa
- 109 Hình ảnh chúc ngủ ngon lãng mạn tặng người yêu
- 109++ Hình ảnh chữ buồn đẹp về tình yêu, cuộc sống Hot nhất