Mời các em theo dõi nội dung bài học về Công thức tính bán kính mặt cầu và bài tập vận dụng do thầy cô trường THCS Bình Chánh biên soạn. Hy vọng sẽ là tài liệu hữu ích giúp các em học tốt và hoàn thành tốt bài tập của mình.
Công thức tính bán kính mặt cầu
S = 4.π.R2
Với: S là kí hiệu diện tích mặt cầu
Bạn đang xem: Công thức tính bán kính mặt cầu và bài tập vận dụng
R là bán kính mặt cầu ngoại tiếp
– Trục đáy: Là đường thẳng đi qua tâm đường tròn ngoại tiếp của đa giác đáy và vuông góc với mặt phẳng chứa đa giác đáy.
– Trung trực của đoạn thẳng: Là đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng đó.
– Mặt trung trực của đoạn thẳng: Mặt phẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng đó.
Công thức tính bán kính mặt cầu của các hình cơ bản
– Tâm và bán kính mặt cầu là hai đại lượng quan trọng để tính diện tích của mặt cầu ngoại tiếp, chính vì vậy xác định tâm và bán kính là thao tác quan trọng để các em có thể tìm được diện tích. Cùng theo dõi cách tìm tâm và cách tính bán kính của mặt cầu ngoại tiếp một số hình.
1. Tính Diện Tích Mặt Cầu Ngoại Tiếp Lăng Trụ
Hình lăng trụ đứng A1A2A3A4.A’1A’2A’3A’4 có hai đáy nội tiếp đường tròn O và O’.
– Tâm mặt cầu: I và I’ (đều là trung điểm của OO’)
– Bán kính mặt cầu ngoại tiếp: R = IA1 = IA2 = ….
– Biết tâm, bán kính, áp dụng công thức để giải các bài tập tính diện tích mặt cầu ngoại tiếp hình lăng trụ đều có các cạnh bằng a,…
2. Tính Diện Tích Mặt Cầu Ngoại Tiếp Hình Chóp
a) Hình chóp đều
* Xác định tâm mặt cầu:
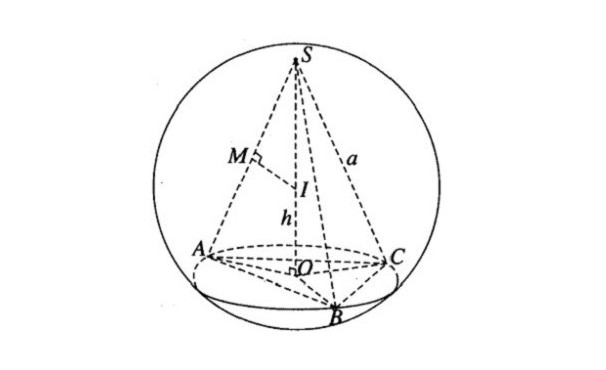
Hình chóp đều S.ABC có:
– O là tâm của đáy => SO là trục đáy
– Trên mặt phẳng (SAO), vẽ d là đường trung trực của SA cắt SA tại giao điểm M, cắt SO tại giao điểm I
=> Tâm mặt cầu ngoại tiếp hình chóp chính là I.
* Tính bán kính mặt cầu ngoại tiếp:
Xét hai tam giác đồng dạng với nhau là SMI và SOA, ta có:
=> R = SI = SA2 : 2.SO = IB = IB = IC (R: Bán kính)
* Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC
=> Sau khi tính được bán kính mặt cầu, ta áp dụng công thức: S = 4.π.R2
b) Hình chóp có cạnh bên vuông góc với mặt phẳng đáy
* Tìm tâm mặt cầu:
Hình chóp SABC có SA vuông góc với mặt đáy (ABC) trong đó mặt đáy ABC nội tiếp đường tròn tâm O
– Từ tâm O ngoại tiếp của đường tròn đáy, vẽ d vuông góc với (ABC) tại O.
– Trong mặt phẳng được tạo bởi đường thẳng d với SA, vẽ đường trung trực d’ của SA, giao với SA tại M, giao với d tại I.
* Tính bán kính mặt cầu ngoại tiếp:
Từ các dữ kiện đã biết, ta có hình chữ nhật MIOB
– Xét tam giác vuông MAI tại M:
R = AI = √(MI2 + MA2) = √[AO2 + (SA/2)2]
Lưu ý: Nếu hình chóp S.ABC có SA vuông góc với mặt đáy (ABC) và tam giác ABC vuông tại B thì tâm đường tròn ngoại tiếp của hình chóp chính là trung điểm của đường SC.
3. Tính Diện Tích Mặt Cầu Ngoại Tiếp Hình Lập Phương, Hình Hộp Chữ Nhật
* Xác định tâm của mặt cầu:
– Tâm của mặt cầu chính là trung điểm của đoạn thẳng AC’ (tâm đối xứng của hình hộp chữ nhật/ hình lập phương).
* Tính bán kính mặt cầu ngoại tiếp:
– Bán kính mặt cầu = 1/2 độ dài đường chéo của hình hộp chữ nhật / hình lập phương.
* Áp dụng công thức tính S để giải các bài tập tính diện tích mặt cầu ngoại tiếp hình lập phương cạnh bằng 1, cạnh bằng 2a,…
Bài tập vận dụng
Bài 1: Phương trình nào sau đây là phương trình mặt cầu ?
A. x2+y2+z2-2x=0
B. x2+y2 – z2+2x-y+1=0
C. 2x2+2y2 = (x+y)2 – z2+2x-1
D. (x+y)2 = 2xy – z2 – 1
Đáp án: A
Giải thích :
Phương trình x2+y2+z2-2ax-2by-2cz+d=0 là phương trình mặt cầu ⇔ a2+b2+c2-d>0
Bài 2: Phương trình nào sau đây không phải là phương trình mặt cầu?
A. x2 + y2 + z2 + 2x – 2y + 1 = 0.
B. x2 + y2 + z2 – 2x = 0.
C. 2x2 + 2y2 = (x + y)2 – z2 + 2x – 1.
D. ( x + y)2 = 2xy – z2 + 1 – 4x.
Đáp án : C
Giải thích :
Bài 3: Cho các phương trình sau:
( x – 1)2 + y2 + z2 = 1
x2 + ( 2y – 1)2+ z2 = 4
x2 + y2 + z2 + 1 = 0
( 2x + 1)2+ ( 2y – 1)2 + 4z2 = 16
Số phương trình là phương trình mặt cầu là:
A. 1
B. 3
C. 4
D. 2
Đáp án : D
Giải thích :
Các phương trình mặt cầu là:
( x – 1)2 + y2 + z2 = 1
x2 + ( 2y – 1)2 + z2 = 4
Bài 4: Mặt cầu ( S ): x2+ y2+ z2– 2x + 10y + 3z + 1 = 0 đi qua điểm có tọa độ nào sau đây?
A. (3; – 2; – 4)
B. ( 2;1;9)
C. ( 4; – 1;0)
D.(- 1;3; – 1)
Đáp án : B
Giải thích :
Thử trực tiếp đáp án, điểm (2; 1; 9) thỏa mãn phương trình mặt cầu.
Bài 5: Mặt cầu ( S ): x2+ y2 + z2 – 4x + 1 = 0 có tọa độ tâm và bán kính R là:
A. I(-2;0;0), R = √3
B. I(2;0;0), R = √3
C. I(0;2;0), R = √3
D. I(2;0;0), R = 3
Đáp án : B
Giải thích :
( S ): x2 + y2 + z2– 4x + 1 = 0
⇔ (x-2)2+y2+z2=3
Phương trình có tâm I (2 ; 0 ; 0), bán kính R=√3
Bài 6: Phương trình mặt cầu có tâm I(-1;2;3), bán kình R=3 là:
A. (x + 1)2+ ( y – 2)2 + ( z + 3)2 = 9
B. ( x + 1)2+ ( y – 2)2+ ( z + 3)2 = 3
C. ( x – 1)2+ ( y + 2)2 + ( z – 3)2 = 9
D. ( x + 1)2+ ( y – 2)2+ ( z + 3)2 = 9
Đáp án : A
Giải thích :
Phương trình mặt cầu tâm I (a; b; c), bán kính R là:
(x-a)2+(y-b)2+(z-c)2=R2
Bài 7: Mặt cầu ( S ): ( x + y)2= 2xy – z2 + 1 – 4x có tâm là:
A. I(2;0;0)
B. I(4;0;0)
C. I(-4;0;0)
D. I(-2;0;0)
Đáp án : D
Giải thích :
(x+y)2=2xy-z2+1-4x ⇔ x2+y2+z2+4x=1
Phương trình có a=-2;b=0;c=0 ⇒ I(-2;0;0)
Bài 8: Mặt cầu có phương trình nào sau đây có tâm là I(-1;1;0) ?
A. x2+ y2 + z2+ 2x – 2y + 1 = 0.
B. x2 + y2+ z2 – 2x + 2y = 0.
C. 2x2 + 2y2 = ( x + y)2 – z2+ 2x – 1 – 2xy.
D. ( x + y)2 = 2xy – z2+ 1 – 4x.
Đáp án : A
Giải thích :
A. x2+ y2 + z2 + 2x – 2y + 1 = 0.
⇔ (x+1)2+(y-1)2+z2=1
Phương trình có tâm I (-1 ; 1 ; 0), bán kính R =1
B. x2 + y2 + z2 – 2x + 2y = 0.
⇔ (x-1)2+(y+1)2+z2=2
Phương trình có tâm I (1 ; -1 ; 0), bán kính R=√2
C. 2x2+ 2y2= ( x + y )2 – z2 + 2x – 1 – 2xy.
⇔ x2+y2+z2-2x+1=0
⇔ (x-1)2+y2+z2=0
Đây không phải là phương trình mặt cầu.
D. (x + y)2= 2xy – z2+ 1 – 4x.
⇔ x2+y2+z2+4x-1=0
⇔(x+2)2+y2+z2=5
Phương trình có tâm I (-2 ; 0 ; 0), bán kính R=√5
Bài 9: Gọi I là tâm mặt cầu ( S ): x2 + y2 + ( z – 2)2= 4. Độ dài OI→ (O là gốc tọa độ) bằng?
A. 1
B. 4
C. 2
D. √2
Đáp án : C
Giải thích :
Mặt cầu ( S ): x2 + y2 + ( z – 2)2= 4 có tâm I (0; 0; 2) ⇒ OI=2
Bài 10: Phương trình mặt cầu có bán kính bằng 3 và tâm là giao điểm của ba trục toạ độ ?
A. x2+ y2 + z2 – 6x = 0.
B. x2 + y2 + z2 – 6y = 0.
C. x2 + y2 + z2 – 6z = 0.
D. x2 + y2 + z2 = 9.
Đáp án : D
Giải thích :
Giao điểm của 3 trục tọa độ là điểm O (0; 0; 0)
Khi đó, phương trình mặt cầu có tâm O (0; 0; 0) và bán kính R = 3 là
x2+y2+z2=9
Bài 11: Trong không gian hệ trục tọa độ Oxyz, phương trình nào sau đây là phương trình mặt cầu, nếu là phương trình mặt cầu, hãy tìm tâm và bán kính của mặt cầu đó
a) (x-2)2+(y+3)2+z2=5
b) x2+y2+z2-2x+4y-6z+1=0
c) 3x2+3y2+3z2-6x+3y+21=0
Hướng dẫn:
a) Phương trình (x-2)2+(y+3)2+z2=5 có dạng
(x-a)2+(y-b)2+(z-c)2=R2 nên là phương trình mặt cầu có tâm
I (2; -3; 0) và bán kính R=√5.
b) Phương trình x2+y2+z2-2x+4y-6z+1=0 có dạng
x2+y2+z2-2ax-2by-2cz+d=0 với a = 1; b = -2; c = 3, d = 1
⇒ a2+b2+c2-d=13>0
Vậy phương trình đã cho là phương trình mặt cầu có tâm I (1; -2; 3) và bán kính R=√13.
c) Phương trình 3x2+3y2+3z2-6x+3y+21=0
⇔ x2+y2+z2-2x+y+7=0
Phương trình có dạng x2+y2+z2-2ax-2by-2cz+d=0 với
a=1;b=(-1)/2;c=0;d=7 ⇒a2+b2+c2-d=(-23)/4<0
Vậy phương trình đã cho không phải là phương trình mặt cầu.
Bài 12: Trong không gian với hệ tọa độ Oxyz, tìm m để mỗi phương trình sau là phương trình mặt cầu.
a) x2+y2+z2-2mx+2(m+1)y-4z+1=0
b) x2+y2+z2-2(m-3)x-4mz+8=0
Hướng dẫn:
a) Phương trình x2+y2+z2-2mx+2(m+1)y-4z+1=0 có
a=m;b=-(m+1); c=2;d=1.
Phương trình là phương trình mặt cầu ⇔ a2+b2+c2-d>0
⇔ m2+(m+1)2+22-1>0⇔2m2+2m+3>0 ⇔m∈R.
b) Phương trình x2+y2+z2-2(m-3)x-4mz+8=0 có a=m-3;
b=0;c=2m;d=8
Phương trình là phương trình mặt cầu ⇔a2+b2+c2-d>0
⇔(m-3)2+4m2-8>0 ⇔5m2-6m+1>0
Bài 13: Trong không gian hệ trục tọa độ Oxyz, tìm tất cả các giá trị thực của tham số m để phương trình x2+y2+z2+2(m+2)x-2(m-3)z+m2-1=0 là phương trình của mặt cầu có bán kính nhỏ nhất.
Hướng dẫn:
Phương trình x2+y2+z2+2(m+2)x-2(m-3)z+m2-1=0 có:
a=-(m+2);b=0;c=m-3;d=m2-1
Phương trình là phương trình mặt cầu ⇔ a2+b2+c2-d>0
⇔ (m+2)2+(m-3)2-m2+1>0 ⇔ m2-2m+14>0 ⇔ m∈R.
Khi đó, bán kính mặt cầu là:
Dấu bằng xảy ra khi m = 1.
Vậy với m = 1 thì mặt cầu có bán kính nhỏ nhất R=√13.
***
Trên đây là nội dung bài học Công thức tính bán kính mặt cầu và bài tập vận dụng do thầy cô trường THCS Bình Chánh biên soạn và tổng hợp. Hy vọng sẽ giúp các em hiểu rõ nội dung bài học và từ đó hoàn thành tốt bài tập của mình. Đồng thời luôn đạt điểm cao trong các bài thi bài kiểm tra sắp tới. Chúc các em học tập thật tốt.
Đăng bởi THCS Bình Chánh trong chuyên mục Học tập
- Cảm nhận của anh (chị) về vùng đất và con người miền cực nam của Tổ quốc qua truyện ngắn Bắt sấu rừng U Minh Hạ lớp 12 (9 Mẫu)
- Anh (chị) hãy bày tỏ quan điểm của mình về ý kiến của nhà văn Pháp La Bơ-ruy-e: “Khi một tác phẩm nâng cao tinh thần ta lên và gợi cho ta những tình cảm cao quý và can đảm, không cần tìm một nguyên tắc nào để đánh giá nó nữa: đó là một cuốn sách hay và do một nghệ sĩ viết ra” lớp 12 (10 Mẫu)
- Buy-phông, nhà văn Pháp nổi tiếng, có viết: “Phong cách chính là người”. Anh (chị) hiểu ý kiến trên như thế nào? lớp 12 (12 Mẫu)
- Một trong những bức thư luận bàn về văn chương, Nguyễn Văn Siêu có viết: “Văn chương […] có loại đáng thờ, có loại không đáng thờ. Loại không đáng thờ là loại chỉ chuyên chú ở văn chương. Loại đáng thờ là loại chuyên chú ở con người. Anh chị hãy phát biểu ý kiến của mình về quan niệm trên lớp 12 (7 Mẫu)
- Viết bài văn trong đó vận dụng tổng hợp ít nhất ba thao tác lập luận, theo chủ đề: một tác phẩm văn học mới ra đời và đáng được nhiều người quan tâm bàn luận lớp 12
- Viết bài văn nghị luận trong đó vận dụng tổng hợp ít nhất ba thao tác lập luận khác nhau lớp 12 (3 Mẫu)