Đường trung tuyến là gì? Tính chất của đường trung tuyến

Cô Nguyễn Thanh Phương 02/06/2023

Mời các em theo dõi nội dung bài học về Đường trung tuyến là gì? Tính chất của đường trung tuyến do thầy cô trường THCS Bình Chánh biên soạn. Hy vọng sẽ là tài liệu hữu ích giúp các em học tốt và hoàn thành tốt bài tập của mình.

Mục lục

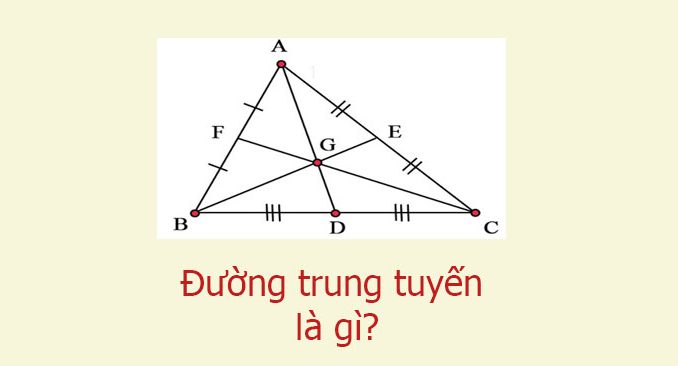
Đường trung tuyến là gì?

Đương trung tuyến trong một tam giác là một đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện.

Mỗi tam giác đều có ba đường trung tuyến.

Bạn đang xem: Đường trung tuyến là gì? Tính chất của đường trung tuyến

Đối với tam giác cân và tam giác đều, mỗi trung tuyến của tam giác chia đôi các góc ở đỉnh với hai cạnh kề có chiều dài bằng nhau.

Tính chất của đường trung tuyến

– Ba đường trung tuyến của một tam giác cùng đồng quy tại một điểm, điểm này được gọi là trọng tâm của tam giác.

Khoảng cách từ trọng tâm của tam giác đến đỉnh bằng 2/3 độ dài đường trung tuyến ứng với đỉnh đó.

– Tam giác vuông là một tam giác đặc biệt với một góc lớn 90 °C, hai cạnh tạo nên góc vuông này luôn vuông góc với nhau, do vậy mà đường trung tuyến của tam giác vuông sẽ mang những tính chát của đường trung tuyến tam giác.

Trong một tam giác bất kì, đường trung tuyến ứng với cạnh huyền của tam giác sẽ có độ dài bằng 1/2 cạnh huyền.

– Mỗi trung tuyến chia diện tích tam giác thành hai phần bằng nhau. Ba trung truyến chia tam giác thành sau tam giác nhỏ với diện tích bằng nhau.

– Đường trung tuyến trong tam giác cân

Đường trung tuyến ứng với cạnh đáy thì vuông góc với cạnh đáy. Và chia tam giác thành hai tam giác bằng nhau.

– Đường trung tuyến trong tam giác đều

Ba đường trung truyến của tam giác đều sẽ chia tam giác đó thành sáu tam giác có diện tích bằng nhau.

Trong tam giác đều đường thẳng đi qua một đỉnh bất kì và đi qua trọng tâm của tam giác sẽ chia tam giác đó thành hai tam giác có diện tích bằng nhau.

Định lí của đường trung tuyến trong tam giác

Định lí 1: Ba đường trung tuyến của một tam giác cùng đi qua một điểm, điểm gặp nhau của ba đường trung tuyến được gọi là trọng tâm của tam giác đó.

Định lí 2: Đường trung tuyến của tam giác chia tam giác thành hai tam giác có diện tích bằng nhau. Va đường trung tuyến chia tam giác thành sáu tam giác nhỏ với diện tích bằng nhau.

Định lí 3: Về vị trí trọng tâm: trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.

Công thức tính độ dài của đường trung tuyến

Độ dài đường trung tuyến của một tam giác được tính thông qua độ dài các cạnh của tam giác và được tính bằng định lý apollonnius.

Trong đó:

a, b, c là các cạnh của tam giác
ma, mb, mc là các đường trung tuyến của tam giác

Bài tập vận dụng về đường trung tuyến

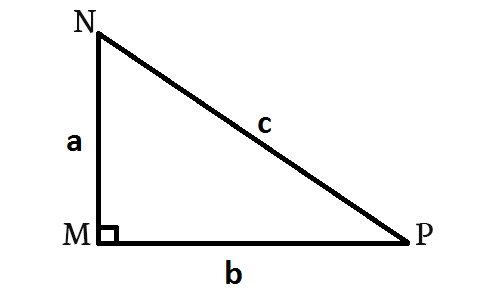
Bài tập 1: Tam giác MNP cho biết NP = 20cm, PM = 16cm, MN = 14cm. Anh/chị hãy tính độ dài các đường trung tuyến của tam giác MNP.

Bài làm:

Gọi:

NP, PM, MN lần lượt là a, b, c
ma, mb, mc lần lượt là độ dài đường trung tuyến từ những đỉnh M, N, P của ∆MNP

Áp dụng công thức tính đường trung tuyến trong tam giác ở phía trên, ta có:

Do độ dài đoạn thẳng là độ dài các đường trung tuyến, vì thế ta có:

Bài tập 2: Cho tam giác MNP cân ở M có MB = MC = 17cm, NP= 16cm. Kẻ trung tuyến MI.

a) Chứng minh: MI ⊥ NP;

b) Tính độ dài MI.

Bài làm:

a. Do MI là đường trung tuyến MNP

=> IP = IN

Mặt khác tam giác MNP cân tại M

=> MI vừa là đường trung tuyến vừa là đường cao

=> MI ⊥ NP

b. Ta có:

NP = 16cm nên NI = PI = 8cm

MN = MP = 17cm

Xét tam giác MIP vuông tại I

Áp dụng Định lý Pitago, ta có:

MP2 = MI2 + IP2

=> 192= MI2 + 82

=> MI2 = 172 – 82 = 225

=> MI = 15cm.

Bài tập 3: Cho tam giác ABC cân tại A, hai đường trung tuyến BE và CD cắt nhau tại G. Kéo dài AG cắt BC tại điểm H. Anh/ chị hãy:

a. So sánh 2 tam giác AHB và AHC.

b. M và N lần lượt là trung điểm của GA và GC. Hãy chứng minh rằng AN, BE, CM đồng quy tại 1 điểm.

Bài làm:

a. Ta có:

BE và CD là 2 đường trung tuyến của tam giác ABC

Mà BE cắt CD tại G

=> Trọng tâm của tam giác ABC là G

Mặt khác AH đi qua G

=> Đường trung tuyến của tam giác ABC là AH

Xét 2 tam giác AHB và AHC, có:

AB = AC

AH chung

HB = HC

⇒ ΔAHB = ΔAHC (cạnh – cạnh – cạnh)

b. Do MA = MG

=> CM là đường trung tuyến của tam giác AGC (1)

Mặt khác NG = NC

=> AN là đường trung tuyến của tam giác AGC (2)

GE là đường trung tuyến của tam giác AGC (3)

Từ (1), (2), (3) = > 3 đường AN, CM, BE đồng quy.

Bài tập 4: Cho tam giác MNK có MK = MN. Gọi E là giao điểm của hai đường trung tuyến NI và KP. Hãy chứng minh:

a)Tam giác NIK và tam giác KPN bằng nhau

b) EN = EK

c) NK < 4EP

Bài làm:

a) Ta có: MK=MN

NI là đường trung tuyến của tam giác MNK

=> NI = ½ MN (1)

KP là đường trung tuyến của tam giác MNK

=> KP = ½ MK (2)

Từ (1), (2) => NI=KP

Xét tam giác NIK và tam giác KPN, ta có:

NK là cạnh chung

NI = KP

góc KNP = góc NKI (tam giác MNK cân tại M)

=> ΔNIK = ΔKPN (cạnh – góc – cạnh)

b) Ta có:

góc INK= góc PKN (Vì ΔNIK = ΔKPN)

Nên tam giác ENK cân tại E

Suy ra EN = EK

c) Xét ΔMNK ta có:

IM = IK (NI là đường trung tuyến)

PM = PN (KP là đường trung tuyến)

Suy ra IP là đường trung bình của tam giác MNK

=> IP = NK/2

Xét tam giác IPE có

IP < PE + EI (bất đẳng thức Cauchy)

PE = PK – EK

=> NK/2 < PK – EK + EI (3)

ΔNIK = ΔKPN => KP = NI (4)

Tam giác ENK cân tại E => EN = EK (5)

Từ (3), (4), (5) => NK/2 < NI – NE + EP

=> NK/2 < 2EP

=> NK < 4EP

***

Trên đây là nội dung bài học Đường trung tuyến là gì? Tính chất của đường trung tuyến do thầy cô trường THCS Bình Chánh biên soạn và tổng hợp. Hy vọng sẽ giúp các em hiểu rõ nội dung bài học và từ đó hoàn thành tốt bài tập của mình. Đồng thời luôn đạt điểm cao trong các bài thi bài kiểm tra sắp tới. Chúc các em học tập thật tốt.

Đăng bởi THCS Bình Chánh trong chuyên mục Học tập