Học Tập Lớp 10 Tin học 10 Kết nối tri thức

Tin học 10 Bài 4 Kết nối tri thức: Hệ nhị phân và dữ liệu số nguyên | Soạn Tin học 10

Trường THCS Bình Chánh 24/07/2023

Mời các em theo dõi nội dung bài học do thầy cô trường Trung học Bình Chánh biên soạn sẽ giúp các em nắm chắc kiến thức nội dung bài học tốt hơn.

Giải Tin học lớp 10 Bài 4: Hệ nhị phân và dữ liệu số nguyên

Khởi động

Bạn đang xem: Tin học 10 Bài 4 Kết nối tri thức: Hệ nhị phân và dữ liệu số nguyên | Soạn Tin học 10

Khởi động trang 20 Tin học 10: Trong hệ thập phân, mỗi số có thể được phân tích thành tổng các luỹ thừa của 10 với hệ số của mỗi số hạng chính là các chữ số tương ứng của số đó. Ví dụ: số 513 có thể viết thành: 5 × 10² + 1 × 10¹ + 3 × 10⁰.

Ta cũng có thể phân tích mỗi số thành tổng của các luỹ thừa của 2, chẳng hạn 13 có thể viết thành: 1 × 2³ + 1 × 2² + 0 × 2¹ + 1 × 2⁰ với các hệ số chỉ là 0 hay 1.

Khi đó, có thể thể hiện 13 bởi dãy 1101 được không? Em hãy cho biết việc thể hiện giá trị của một số bằng dãy bit có lợi gì?

Trả lời:

Có thể thể hiện 13 bởi dãy 1101. Việc thể hiện giá trị của một số bằng dãy bit giúp biểu diễn được con số trong máy tính.

1. Hệ nhị phân và biểu diễn số nguyên

Hoạt động

Hoạt động 1 trang 20 Tin học 10: Biểu diễn một số dưới dạng tổng luỹ thừa của 2

Em hãy viết số 19 thành một tổng các luỹ thừa của 2?

Gợi ý: hãy lập danh sách các luỹ thừa của 2 như 16, 8, 4, 2, 1 và tách dần khỏi 19 cho đến hết.

Trả lời:

19 = 2⁴ + 2¹+ 2⁰

Câu hỏi

Câu hỏi 1 trang 21 Tin học 10: Em hãy đổi các số sau từ hệ thập phân sang hệ nhị phân

a) 13. b) 155. c) 76.

Trả lời:

13₁₀= 1 × 2³+ 1 × 2² + 0 × 2¹+ 1 × 2⁰ = 1101₂

155₁₀= 1 × 2⁷ + 0 × 2⁶ + 0 × 2⁵ + 1 × 2⁴ + 1 × 2³+ 0 × 2² + 1 × 2¹+ 1 × 2⁰= 10011011₂

76 = 1 × 2⁶ + 0 × 2⁵+ 0 × 2⁴ + 1 × 2³+ 1 × 2² + 0 × 2¹+ 0 × 2⁰= 1001100₂

Câu hỏi 2 trang 21 Tin học 10: Em hãy đổi các số sau từ hệ nhị phân sang hệ thập phân

a) 110011. b) 10011011. c) 1001110.

Trả lời:

a) 110011 = 1 × 2⁵ + 1 × 2⁴ + 0 × 2³+ 0 × 2² + 1 × 2¹+ 1 × 2⁰= 51

b) 10011011 = 1 × 2⁷ +0 × 2⁶ + 0 × 2⁵ + 1 ×2⁴ + 1 × 2³+ 0 × 2² + 1 × 2¹+ 1 × 2⁰= 155

c) 1001110 = 1 × 2⁶ + 0 × 2⁵+ 0 ×2⁴ + 1 × 2³+ 1 × 2² + 1 × 2¹+ 0 × 2⁰= 78

2. Các phép tính số học trong hệ nhị phân

Hoạt động

Hoạt động 2 trang 22 Tin học 10: Hãy chuyển các toán hạng của hai phép tính sau ra hệ nhị phân để chuẩn bị kiểm tra kết quả thực hiện các phép toán trong hệ nhị phân. (Ví dụ: 3 + 4 = 7 sẽ được chuyển thành 11 + 100 = 111).

a) 26 + 27 = 53. b) 5 × 7 = 35.

Trả lời:

a) 26 + 27= 53

00011010 + 00011011 = 00110101

b) 5 × 7 = 35

00000101 × 00000111 = 00100011

Câu hỏi

Câu hỏi trang 23 Tin học 10: Hãy thực hiện các phép tính sau trong hệ nhị phân:

a) 101101 + 11001. b) 100111 × 1011.

Trả lời:

a) 101101 + 11001 = 1000110

b) 100111 × 1011 = 110101101

Luyện tập

Luyện tập 1 trang 23 Tin học 10: Hãy thực hiện các phép tính sau đây theo quy trình Hình 4.4

a) 125 + 7. b) 250 + 75. c) 75 + 112.

Trả lời:

a) 125 + 7 = 01111101 + 00000111 = 10000100 = 132.

b) 250 + 75 = 11111010 + 01001011 = 101000101 = 325.

c) 75 + 112 = 01001011 + 01110000 = 10111011 = 187.

Luyện tập 2 trang 23 Tin học 10: Em hãy thực hiện các phép tính sau đây theo quy trình Hình 4.4

a) 15 × 6. b) 11 × 9. c) 125 × 4.

Trả lời:

a) 15 × 6 = 1111 × 110 = 1010000 = 80.

b) 11 × 9 = 1011 × 1001 = 1011010 = 90.

c) 125 × 4 = 1111101 × 100 = 111110100 = 500.

Vận dụng

Vận dụng 1 trang 23 Tin học 10: Em hãy tìm hiểu trên Internet hoặc các tài liệu khác cách đổi phần thập phân của một số trong hệ thập phân sang hệ đếm nhị phân.

Trả lời:

Cách đổi phần thập phân của một số trong hệ thập phân sang hệ đếm nhị phân: đối với phần lẻ của số thập phân, số lẻ được nhân với 2. Phần nguyên của kết quả sẽ là bit nhị phân, phần lẻ của kết quả lại tiếp tục nhân 2 cho đến khi phần lẻ của kết quả bằng 0.

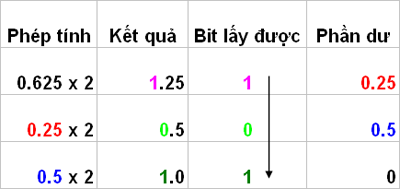
Ví dụ 1: Chuyển số 0.625₁₀ sang hệ nhị phân

– 0.625 × 2 = 1.25, lấy số 1, phần lẻ 0.25

– 0.25 × 2 = 0.5, lấy số 0, phần lẻ 0.5

– 0.5 × 2 = 1.0, lấy số 1, phần lẻ 0. Kết thúc phép chuyển đổi.

Vậy kết quả 0.625₁₀ = 0.101₂

Ví dụ 2: Đổi số 9.625₁₀ sang hệ nhị phân

– Phần nguyên 9 đổi sang hệ nhị phân là 1001

– Phần lẻ 0.625 đổi sang hệ nhị phân là 0.101

Vậy số 9.625₁₀ = 1001.101₂

Vận dụng 2 trang 23 Tin học 10: Em hãy tìm hiểu mã bù 2 với hai nội dung:

a) Mã bù 2 được lập như thế nào?

b) Mã bù 2 được dùng để làm gì?

Trả lời:

a) Mã bù 2 (tiếng Anh: two’s complement) là một số trong hệ nhị phân là bù đúng (true complement) của một số khác. Một số bù 2 có được do đảo tất cả các bit có trong số nhị phân (đổi 1 thành 0 và ngược lại) rồi thêm 1 vào kết quả vừa đạt được. Thực chất, số biểu diễn ở dạng bù 2 là số biểu diễn ở bù 1 rồi sau đó cộng thêm 1. Trong quá trình tính toán bằng tay cho nhanh người ta thường sử dụng cách sau: từ phải qua trái giữ 1 đầu tiên và các số còn lại bên trái số 1 lấy đảo lại (chỉ áp dụng cho số có bit cực phải là 1).

b) Mã bù 2 thường được sử dụng để biểu diễn số âm trong máy tính. Theo phương pháp này, bit cực trái (là bit nằm bên trái cùng của byte) được sử dụng làm bit dấu (sign bit – là bit tượng trưng cho dấu của số) với quy ước: nếu bit dấu là 0 thì số là số dương, còn nếu nó là 1 thì số là số âm. Ngoài bit dấu này ra, các bit còn lại được dùng để biểu diễn độ lớn của số.

Xem thêm lời giải bài tập Tin học lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:

Bài 5: Dữ liệu lôgic

Bài 6: Dữ liệu âm thanh và hình ảnh

Bài 7: Thực hành sử dụng thiết bị số thông dụng

Bài 8: Mạng máy tính trong cuộc sống hiện đại

Bài 9: An toàn trên không gian mạng

Xem thêm tài liệu Tin học lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:

Lý thuyết Bài 4: Hệ nhị phân và dữ liệu số nguyên

Đăng bởi: THCS Bình Chánh

Chuyên mục: Tin học 10 Kết nối tri thức