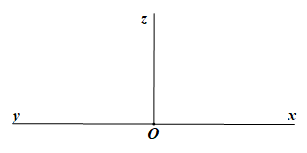Toán 7 Bài 11 Kết nối tri thức: Định lí và chứng minh định lí
Mời các em theo dõi nội dung bài học do thầy cô trường Trung học Bình Chánh biên soạn sẽ giúp các em nắm chắc kiến thức nội dung bài học tốt hơn.
Giải bài tập Toán 7 Bài 11: Định lí và chứng minh định lí
Bạn đang xem: Toán 7 Bài 11 Kết nối tri thức: Định lí và chứng minh định lí
Mở đầu
Mở đầu trang 55 Toán 7 Tập 1: Trong Bài 10, ta đã dùng cách đo đạc để kiểm nghiệm tính chất sau là đúng:
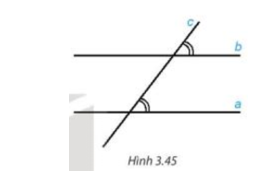
“Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau” (H.3.45).
Tuy nhiên, đo đạc chỉ cho ta kết quả gần đúng và chỉ trong một trường hợp cụ thể.
Vậy có cách nào để chắc chắn rằng tính chất đó đúng cho mọi trường hợp không?
Lời giải:
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
|
GT |
a // b; c cắt a tại A, c cắt b tại B; Hai góc và là hai góc đồng vị. |
|
KL |
|
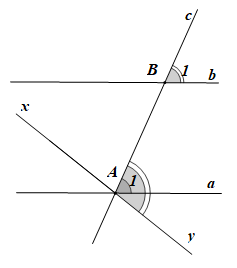
Chứng minh (Hình vẽ trên):
+) Qua A kẻ đường thẳng xy sao cho
Mà hai góc này ở vị trí đồng vị nên xy // b (dấu hiệu nhận biết hai đường thẳng song song).
Ta có a // b, xy // b nên ba đường thẳng xy // a (hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau).
Do đó qua điểm A ta có đường hai đường thẳng a và xy cùng song song với đường thẳng b.
Theo Tiên đề Euclid suy ra đường thẳng xy trùng với đường thẳng a.
Suy ra hay
Vậy
Định lí. Giả thiết và kết luận của định lí
Giải Toán 7 trang 56 Tập 1
Luyện tập 1 trang 56 Toán 7 Tập 1: Vẽ hình và viết giả thiết, kết luận của định lí: “Hai góc đối đỉnh thì bằng nhau”.
Lời giải:
Trong định lí: “Hai góc đối đỉnh thì bằng nhau”, thì có:
Giả thiết là: “hai góc đối đỉnh”.
Kết luận là: “bằng nhau”.
Ta có thể viết giả thiết và kết luận của định lí trên bằng kí hiệu như sau:
|
GT |
xx’, yy’ là các đường thẳng, xx’ cắt yy’ tại A; và là hai góc đối đỉnh. |
|
KL |
|
Thế nào là chứng minh định lí
Giải Toán 7 trang 57 Tập 1
Luyện tập 2 trang 57 Toán 7 Tập 1: Em hãy chứng minh định lí: “Hai góc kề bù bằng nhau thì mỗi góc là một góc vuông”.
Lời giải:
|
GT |
và là hai góc kề bù; |
|
KL |
|
Chứng minh (Hình vẽ trên):
Theo giả thiết ta có và là hai góc kề bù nên (tính chất hai góc kề bù).
Mà ; .
Hay
Do đó
Suy ra
Vậy
Tranh luận trang 57 Toán 7 Tập 1:
Hình tròn: Hai góc đối đỉnh thì chắc chắn bằng nhau rồi. Liệu hai góc bằng nhau thì có đối đỉnh không nhỉ?
Hình vuông: Tớ nghĩ đó là điều không đúng! Nhưng làm thế nào để khẳng định điều đó không đúng nhỉ?
Em có ý kiến gì về hai ý kiến trên?
Lời giải:
Nhận xét: Hai góc bằng nhau chưa chắc đã là hai góc đối đỉnh.
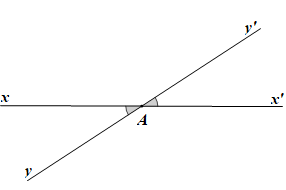
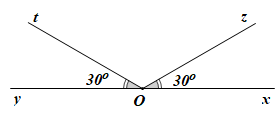
Ví dụ như hình vẽ sau:
Trong hình vẽ trên, hai góc xOz và góc tOy đều có số đo bằng 30° nhưng không phải là hai góc đối đỉnh do tia Oz là cạnh của góc xOz không là tia đối của tia Ot là cạnh của góc tOy.
Bài tập
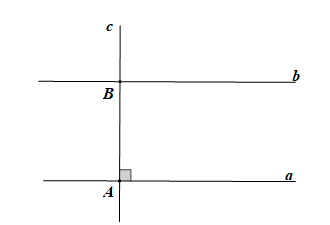
Bài 3.24 trang 57 Toán 7 Tập 1: Có thể coi định lí “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau” được suy ra trực tiếp từ định lí về dấu hiệu nhận biết hai đường thẳng song song không? Suy ra như thế nào?
Lời giải:
Định lí “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau” có thể được suy ra trực tiếp từ định lí về dấu hiệu nhận biết hai đường thẳng song song.
|
GT |
c cắt a tại A, c cắt b tại B; Góc aAc và góc bBc là hai góc đồng vị. |
|
KL |
a // b. |
Chứng minh (Hình vẽ trên):
Theo giả thiết ta có tại A nên tại B nên
Suy ra
Mà hai góc này ở vị trí đồng vị.
Do đó a // b (dấu hiệu nhận biết hai đường thẳng song song).
Vậy a // b.
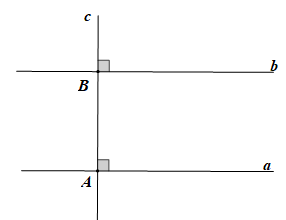
Bài 3.25 trang 57 Toán 7 Tập 1: Hãy chứng minh định lí nói ở Ví dụ trang 56: “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại”. Trong chứng minh đó ta đã sử dụng những điều đúng đã biết nào?
Lời giải:
|
GT |
a // b, c cắt a tại A, c cắt b tại B; Góc aAc và góc bBc là hai góc đồng vị. |
|
KL |
|
+) Chứng minh (Hình vẽ trên):
Theo giả thiết ta có tại A nên
Từ a // b suy ra (hai góc đồng vị).
Mà do đó
Suy ra tại B.
Vậy
+) Trong chứng minh trên ta đã sử dụng những điều đúng đã biết sau:
– Hai đường thẳng vuông góc với nhau tạo thành các góc có số đo bằng 90°.
– Một đường thắng cắt hai đường thẳng song song với nhau tạo thành cặp góc đồng vị có số đo bằng nhau.
Bài 3.26 trang 57 Toán 7 Tập 1: Cho góc xOy không phải góc bẹt. Khẳng định nào sau đây là đúng?
(1) Nếu Ot là tia phân giác của góc xOy thì
(2) Nếu tia Ot thỏa mãn thì Ot là tia phân giác của góc xOy.
Nếu có khẳng định không đúng, hãy nêu ví dụ cho thấy khẳng định đó không đúng.
(Gợi ý: Xét tia đối của một tia phân giác).
Lời giải:
Khẳng định (1) là khẳng định đúng, khẳng định (2) là khẳng định không đúng.
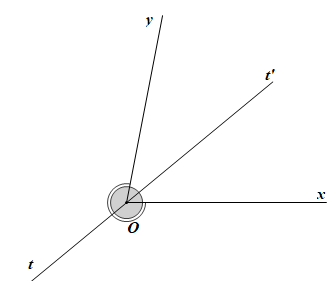
Ví dụ cho thấy khẳng định (2) không đúng:
Trong hình vẽ trên ta thấy tia Ot thoả mãn điều kiện nhưng không phải là tia phân giác của góc xOy.
Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Luyện tập chung trang 58
Bài tập cuối chương 3 trang 59
Bài 12: Tổng các góc trong một tam giác
Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác
Luyện tập chung trang 68, trang 69
Xem thêm tài liệu Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Lý thuyết Bài 11. Định lí và chứng minh định lí
Đăng bởi: THCS Bình Chánh
Chuyên mục: Giải Toán 7 Kết nối tri thức
- Giải Bài 9.29 trang 81 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 9.30 trang 81 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.33 trang 21 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.27 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.28 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.29 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống