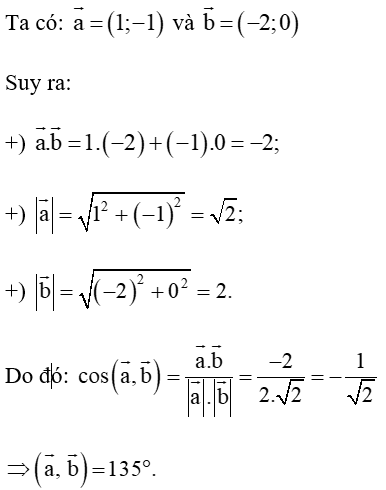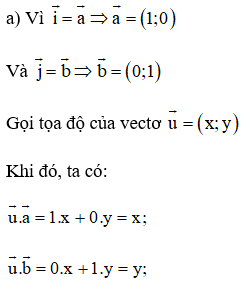Toán 10 Kết nối tri thức Bài tập cuối chương 4 | Giải Toán lớp 10

Trường THCS Bình Chánh 24/07/2023

Mời các em theo dõi nội dung bài học do thầy cô trường Trung học Bình Chánh biên soạn sẽ giúp các em nắm chắc kiến thức nội dung bài học tốt hơn.

Giải bài tập Toán 10 Bài tập cuối chương 4

A. Trắc nghiệm

Bạn đang xem: Toán 10 Kết nối tri thức Bài tập cuối chương 4 | Giải Toán lớp 10

Giải Toán 10 trang 71 Tập 1

Bài 4.27 trang 71 Toán 10 Tập 1: Trong mặt phẳng tọa độ, cặp vectơ nào sau đây có cùng phương?

A. $\vec{u} = (2; 3)$ và $\vec{v} = (\frac{1}{2}; 6)$ .

B. $\vec{a} = (\sqrt{2}; 6)$ và $\vec{b} = (1; 3 \sqrt{2})$ .

C. $\vec{i} = (0; 1)$ và $\vec{j} = (1; 0)$ .

D. $\vec{c} = (1; 3)$ và $\vec{d} = (2; - 6)$ .

Lời giải

+) Xét hai vectơ $\vec{u} = (2; 3)$ và $\vec{v} = (\frac{1}{2}; 6)$ :

Ta có: $\frac{2}{\frac{1}{2}} \neq \frac{3}{6}$ suy ra hai vectơ $\vec{u}$ và $\vec{v}$ không cùng phương.

Do đó A sai.

+) Xét hai vectơ $\vec{a} = (\sqrt{2}; 6)$ và $\vec{b} = (1; 3 \sqrt{2})$ :

Ta có: $\frac{\sqrt{2}}{1} = \frac{6}{3 \sqrt{2}} = \sqrt{2}$ suy ra hai vectơ $\vec{a}$ và $\vec{b}$ cùng phương.

Do đó B đúng.

+) Xét hai vectơ $\vec{i} = (0; 1)$ và $\vec{j} = (1; 0)$ :

Đây là hai vectơ đơn vị nên chúng vuông góc với nhau suy ra hai vectơ $\vec{i}$ và $\vec{j}$ không cùng phương.

Do đó C sai.

+) Xét hai vectơ $\vec{c} = (1; 3)$ và $\vec{d} = (2; - 6)$ :

Ta có: $\frac{1}{2} \neq \frac{3}{- 6}$ suy ra hai vectơ $\vec{c}$ và $\vec{d}$ không cùng phương.

Do đó D sai.

Vậy ta chọn phương án B.

Bài 4.28 trang 71 Toán 10 Tập 1: Trong mặt phẳng tọa độ, cặp vectơ nào sau đây vuông góc với nhau?

A. $\vec{u} = (2; 3)$ và $\vec{v} = (4; 6)$ .

B. $\vec{a} = (1; - 1)$ và $\vec{b} = (- 1; 1)$ .

C. $\vec{z} = (a; b)$ và $\vec{t} = (- b; a)$ .

D. $\vec{n} = (1; 1)$ và $\vec{k} = (2; 0)$ .

Lời giải

+) Xét hai vectơ $\vec{u} = (2; 3)$ và $\vec{v} = (4; 6)$ :

Ta có: $\vec{u} . \vec{v} = 2.4 + 3.6 = 8 + 18 = 26 \neq 0.$

Suy ra hai vectơ $\vec{u}, \vec{v}$ không vuông góc. Do đó A sai.

+) Xét hai vectơ $\vec{a} = (1; - 1)$ và $\vec{b} = (- 1; 1)$ :

Ta có: $\vec{a} . \vec{b} = 1. (- 1) + (- 1) .1 = - 1 + (- 1) = - 2 \neq 0.$

Suy ra hai vectơ $\vec{a}, \vec{b}$ không vuông góc với nhau. Do đó B sai.

+) Xét hai vectơ $\vec{z} = (a; b)$ và $\vec{t} = (- b; a)$ :

Ta có: $\vec{z} . \vec{t} = a . (- b) + b . a = - a b + a b = 0.$

Suy ra hai vectơ $\vec{z}, \vec{t}$ vuông góc với nhau. Do đó C đúng.

+) Xét hai vectơ $\vec{n} = (1; 1)$ và $\vec{k} = (2; 0)$ :

Ta có: $\vec{n} . \vec{k} = 1.2 + 1.0 = 2 + 0 = 2 \neq 0.$

Suy ra hai vectơ $\vec{n}, \vec{k}$ không vuông góc. Do đó D sai.

Vậy ta chọn phương án C.

Bài 4.29 trang 71 Toán 10 Tập 1: Trong mặt phẳng tọa độ, vectơ nào sau đây có độ dài bằng 1?

A. $\vec{a} = (1; 1)$ .

B. $\vec{b} = (1; - 1)$ .

C. $\vec{c} = (2; \frac{1}{2})$ .

D. $\vec{d} = (\frac{1}{\sqrt{2}}; \frac{- 1}{\sqrt{2}})$ .

Lời giải

+) Xét vectơ $\vec{a} = (1; 1) \Rightarrow |\vec{a}| = \sqrt{1^{2} + 1^{2}} = \sqrt{2} \neq 1$ . Do đó A sai.

+) Xét vectơ $\vec{b} = (1; - 1) \Rightarrow |\vec{b}| = \sqrt{1^{2} + {(- 1)}^{2}} = \sqrt{2} \neq 1$ . Do đó B sai.

+) Xét vectơ $\vec{c} = (2; \frac{1}{2}) \Rightarrow |\vec{c}| = \sqrt{2^{2} + {(\frac{1}{2})}^{2}} = \sqrt{\frac{17}{4}} \neq 1$ . Do đó C sai.

+) Xét vectơ $\vec{d} = (\frac{1}{\sqrt{2}}; \frac{- 1}{\sqrt{2}}) \Rightarrow |\vec{d}| = \sqrt{{(\frac{1}{\sqrt{2}})}^{2} + {(\frac{- 1}{\sqrt{2}})}^{2}} = 1$ . Do đó D đúng.

Vậy ta chọn phương án D.

Bài 4.30 trang 71 Toán 10 Tập 1: Góc giữa vectơ $\vec{a} = (1; - 1)$ và vectơ $\vec{b} = (- 2; 0)$ có số đo bằng:

A. 90°.

B. 0°.

C. 135°.

D. 45°.

Lời giải

Vậy ta chọn phương án C.

Bài 4.31 trang 71 Toán 10 Tập 1: Khẳng định nào sau đây là đúng?

A. $(\vec{a} . \vec{b}) \vec{c} = \vec{a} (\vec{b} . \vec{c}) .$

B. ${(\vec{a} . \vec{b})}^{2} = {\vec{a}}^{2} . {\vec{b}}^{2} .$

C. $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . \sin (\vec{a}, \vec{b}) .$

D. $\vec{a} (\vec{b} - \vec{c}) = \vec{a} . \vec{b} - \vec{a} . \vec{c} .$

Lời giải

+) Xét phương án A:

$(\vec{a} . \vec{b}) \vec{c} = [|\vec{a}| . |\vec{b}| . c o s (\vec{a}, \vec{b})] \vec{c}$ ;

$\vec{a} (\vec{b} . \vec{c}) = \vec{a} [|\vec{b}| . |\vec{c}| . c o s (\vec{b}, \vec{c})]$ .

Suy ra $(\vec{a} . \vec{b}) \vec{c} \neq \vec{a} (\vec{b} . \vec{c}) .$ Do đó A sai.

+) Xét phương án B:

${(\vec{a} . \vec{b})}^{2} = {[|\vec{a}| . |\vec{b}| . c o s (\vec{a}, \vec{b})]}^{2} = {|\vec{a}|}^{2} . {|\vec{b}|}^{2} . c o s^{2} (\vec{a}, \vec{b})$

${\vec{a}}^{2} . {\vec{b}}^{2} = {|\vec{a}|}^{2} . {|\vec{b}|}^{2} .$

Suy ra ${(\vec{a} . \vec{b})}^{2} = {\vec{a}}^{2} . {\vec{b}}^{2}$ chỉ đúng khi $c o s^{2} (\vec{a}, \vec{b}) = 1$ . Do đó B sai.

+) Xét phương án C:

$\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . c os (\vec{a}, \vec{b}) \neq |\vec{a}| . |\vec{b}| . \sin (\vec{a}, \vec{b}) .$

Do đó C sai.

+)Xét phương án D:

Theo tính chất của tích vô hướng ta có:

$\vec{a} (\vec{b} - \vec{c}) = \vec{a} . \vec{b} - \vec{a} . \vec{c}$ (tính chất phân phối đối với phép trừ).

Vậy ta chọn phương án D.

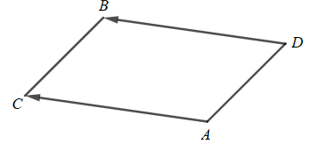
Bài 4.32 trang 71 Toán 10 Tập 1: Cho hình vuông ABCD có cạnh a. Khẳng định nào sau đây là đúng?

A. $(\vec{A B}, \vec{B D}) = 45 ° .$

B. $\vec{A C} . \vec{B C} = a^{2} .$

C. $\vec{A C} . \vec{B D} = a^{2} \sqrt{2} .$

D. $\vec{B A} . \vec{B D} = - a^{2} .$

Lời giải

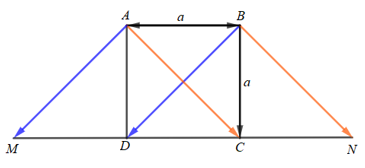
ABCD là hình vuông cạnh a nên AB = BC = CD = DA = a;

Và $B D = A C = \sqrt{A B^{2} + B C^{2}} = \sqrt{a^{2} + a^{2}} = a \sqrt{2}$

Lấy điểm M và N sao cho ABDM, ABNC là các hình bình hành.

+) Vì ABDM là hình bình hành nên $\vec{B D} = \vec{A M}$

$\Rightarrow (\vec{A B}, \vec{B D}) = (\vec{A B}, \vec{A M}) = \hat{B A M} = 90 ° + 45 ° = 135 ° .$

Do đó A sai.

+) Vì ABNC là hình bình hành nên $\vec{A C} = \vec{B N}$

$\Rightarrow (\vec{A C}, \vec{B C}) = (\vec{B N}, \vec{B C}) = \hat{C B N} = 45 °$

$\Rightarrow \vec{A C} . \vec{B C} = A C . B C . c o s \hat{C B F} = a \sqrt{2} . a . c {os45}^{0} = a^{2} .$

Do đó B đúng.

+) Ta có $A C ⊥ B D \Rightarrow \vec{A C} ⊥ \vec{B D} \Rightarrow \vec{A C} . \vec{B D} = 0$ .

Do đó C sai.

+) Ta có:

$\vec{B A} . \vec{B D} = B A . B D . \cos (\vec{B A}, \vec{B D}) = B A . B D . \cos \hat{A B D} = a . a \sqrt{2} . c {os45}^{0} = a^{2} .$

Do đó D sai.

B. Tự luận

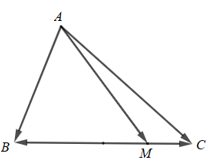
Bài 4.33 trang 71 Toán 10 Tập 1: Trên cạnh BC của tam giác ABC lấy điểm M sao cho MB = 3MC.

a) Tìm mối liên hệ giữa hai vectơ $\vec{M B}$ và $\vec{M C}$ .

b) Biểu thị vectơ $\vec{A M}$ theo hai vectơ $\vec{A B}$ và $\vec{A C} .$

Lời giải

a) Vì điểm M nằm trên cạnh BC nên hai vectơ $\vec{M B}$ và $\vec{M C}$ là hai vectơ ngược hướng.

Lại có MB = 3MC nên $\vec{M B} = - 3 \vec{M C}$ .

Vậy $\vec{M B} = - 3 \vec{M C} .$

b) Theo câu a: $\vec{M B} = - 3 \vec{M C} \Rightarrow \vec{M B} = 3 \vec{C M} = \frac{3}{4} \vec{C B} = - \frac{3}{4} \vec{B C} .$

Ta có: $\vec{A M} = \vec{A B} + \vec{B M} = \vec{A B} - \vec{M B}$

$= \vec{A B} + \frac{3}{4} \vec{B C} = \vec{A B} + \frac{3}{4} (\vec{A C} - \vec{A B})$ (quy tắc ba điểm)

$= \vec{A B} + \frac{3}{4} \vec{A C} - \frac{3}{4} \vec{A B} = \frac{1}{4} \vec{A B} + \frac{3}{4} \vec{A C}$

Vậy $\vec{A M} = \frac{1}{4} \vec{A B} + \frac{3}{4} \hat{A C}$ .

Giải Toán 10 trang 72 Tập 1

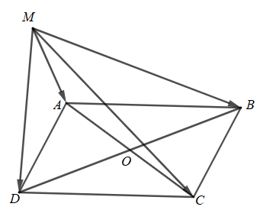
Bài 4.34 trang 72 Toán 10 Tập 1: Cho hình bình hành ABCD. Chứng minh rằng với mọi điểm M, ta có:

$\vec{M A} + \vec{M C} = \vec{M B} + \vec{M D}$

Lời giải

Gọi O là giao điểm của AC và BD.

Suy ra O là trung điểm của AC và BD.

$\Rightarrow \vec{O A} + \vec{O C} = \vec{0}$ và $\vec{O B} + \vec{O D} = \vec{0}$

Ta có:

$\vec{M A} + \vec{M C} = \vec{M O} + \vec{O A} + \vec{M O} + \vec{O C} = 2 \vec{M O} + (\vec{O A} + \vec{O C}) = 2 \vec{M O}$

(Vì $\vec{O A} + \vec{O C} = \vec{0}$ )

$\vec{M B} + \vec{M D} = \vec{M O} + \vec{O B} + \vec{M O} + \vec{O D} = 2 \vec{M O} + (\vec{O B} + \vec{O D}) = 2 \vec{M O}$

(Vì $\vec{O B} + \vec{O D} = \vec{0}$ )

Suy ra $\vec{M A} + \vec{M C} = \vec{M B} + \vec{M D} .$

Vậy $\vec{M A} + \vec{M C} = \vec{M B} + \vec{M D} .$

Bài 4.35 trang 72 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho A(2; 1), B(‒2; 5) và C(‒5; 2).

a) Tìm tọa độ của các vectơ $\vec{B A}$ và $\vec{B C} .$

b) Chứng minh rằng A, B, C là ba đỉnh của một tam giác vuông. Tính diện tích và chu vi của tam giác đó.

c) Tìm tọa độ trọng tâm G của tam giác ABC.

d) Tìm tọa độ của điểm D sao cho tứ giác BCAD là một hình bình hành.

Lời giải

a) Với A(2; 1), B(‒2; 5) và C(‒5; 2) ta có: $\vec{B A} = (4; - 4)$ và $\vec{B C} = (- 3; - 3) .$

b) Ta có:

$\vec{B A} . \vec{B C} = 4. (- 3) + (- 4) . (- 3) = - 12 + 12 = 0$

$\Rightarrow \vec{B A} ⊥ \vec{B C}$

$\Rightarrow B A ⊥ B C$

$\Rightarrow Δ A B C$ vuông tại B.

Do $\vec{B A} = (4; - 4) \Rightarrow B A = \sqrt{4^{2} + {(- 4)}^{2}} = 4 \sqrt{2}$ ;

$\vec{B C} = (- 3; - 3) \Rightarrow B C = \sqrt{{(- 3)}^{2} + {(- 3)}^{2}} = 3 \sqrt{2}$ .

Với A(2; 1) và C(‒5; 2) ta có:

$\vec{A C} = (- 7; 1) \Rightarrow A C = \sqrt{{(- 7)}^{2} + 1^{2}} = \sqrt{50} = 5 \sqrt{2}$

Diện tích tam giác vuông ABC là:

$S_{Δ A B C} = \frac{1}{2} . A B . B C = \frac{1}{2} .4 \sqrt{2} .3 \sqrt{2} = 12$ (đơn vị diện tích)

Chu vi tam giác ABC là:

AB + BC + AC = $4 \sqrt{2} + 3 \sqrt{2} + 5 \sqrt{2} = 12 \sqrt{2}$ (đơn vị độ dài)

c) Với A(2; 1), B(‒2; 5) và C(‒5; 2) ta có tọa độ trọng tâm G của tam giác ABC là:

$\{\begin{cases} x_{G} = \frac{2 + (- 2) + (- 5)}{3} = \frac{- 5}{3} \\ y_{G} = \frac{1 + 5 + 2}{3} = \frac{8}{3} \end{cases} \Rightarrow G (\frac{- 5}{3}; \frac{8}{3})$

Vậy tọa độ trọng tâm của tam giác ABC là: $G (\frac{- 5}{3}; \frac{8}{3}) .$

Để tứ giác BCAD là hình bình hành thì $\vec{A C} = \vec{D B}$

Giả sử D(x; y) là điểm cần tìm.

Với A(2; 1), B(‒2; 5) và C(‒5; 2) ta có: $\vec{A C} = (- 7; 1)$ và $\vec{D B} = (- 2 - x; 5 - y)$

Do đó $\vec{A C} = \vec{D B}$

$\Leftrightarrow \{\begin{cases} - 2 - x = - 7 \\ 5 - y = 1 \end{cases} \Leftrightarrow \{\begin{cases} x = 5 \\ y = 4 \end{cases} \Rightarrow D (5; 4)$ .

Vậy với D(5;4) thì tứ giác BCAD là một hình bình hành.

Bài 4.36 trang 72 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho A(1; 2), B(3; 4), C(‒1; ‒2) và D(6; 5).

a) Tìm tọa độ của các vectơ $\vec{A B}$ và $\vec{C D}$ .

b) Hãy giải thích tại sao các vectơ $\vec{A B}$ và $\vec{C D}$ cùng phương.

c) Giả sử E là điểm có tọa độ (a; 1). Tìm a để vectơ $\vec{A C}$ và $\vec{B E}$ cùng phương.

d) Với a tìm được, hãy biểu thị vectơ $\vec{A E}$ theo các vectơ $\vec{A B}$ và $\vec{A C}$ .

Lời giải

a) Với A(1; 2), B(3; 4), C(‒1; ‒2) và D(6; 5) ta có: $\vec{A B} = (2; 2)$ và $\vec{C D} = (7; 7)$ .

b) Xét hai vectơ $\vec{A B} = (2; 2)$ và $\vec{C D} = (7; 7)$ :

Ta có: $\frac{7}{2} = \frac{7}{2}$ nên hai vectơ $\vec{A B}$ và $\vec{C D}$ cùng phương.

Vậy hai vectơ $\vec{A B}$ và $\vec{C D}$ cùng phương.

c) Với A(1; 2), B(3; 4), C(‒1; ‒2) và E(a; 1) ta có: $\vec{A C} = (- 2; - 4)$ và $\vec{B E} = (a - 3; - 3)$

Hai vectơ $\vec{A C}$ và $\vec{B E}$ cùng phương khi và chỉ khi $\frac{a - 3}{- 2} = \frac{- 3}{- 4}$

$\Leftrightarrow$ (‒ 4).(a – 3) = (‒3). (‒2)

$\Leftrightarrow$ ‒ 4a + 12 = 6

$\Leftrightarrow$ 4a = 6

$\Leftrightarrow a = \frac{3}{2} .$

Vậy $a = \frac{3}{2}$ thì hai vectơ $\vec{A C}$ và $\vec{B E}$ cùng phương.

d) Với $a = \frac{3}{2} \Rightarrow E (\frac{3}{2}; 1)$

Với A(1; 2) và $E (\frac{3}{2}; 1)$ $\Rightarrow \vec{A E} = (\frac{1}{2}; - 1)$

Ta có: $\vec{A B} = (2; 2)$ và $\vec{A C} = (- 2; - 4)$

Tồn tại hai số thực m và n thỏa mãn: $\vec{A E} = m \vec{A B} + n \vec{A C}$

$\Leftrightarrow \{\begin{cases} \frac{1}{2} = m .2 + n . (- 2) \\ - 1 = m .2 + n . (- 4) \end{cases} \Leftrightarrow \{\begin{cases} 2 m - 2 n = \frac{1}{2} \\ 2 m - 4 n = - 1 \end{cases} \Leftrightarrow \{\begin{cases} m = 1 \\ n = \frac{3}{4} \end{cases}$

$\Rightarrow \vec{A E} = \vec{A B} + \frac{3}{4} \vec{A C}$

Vậy $\vec{A E} = \vec{A B} + \frac{3}{4} \vec{A C}$ .

Bài 4.37 trang 72 Toán 10 Tập 1: Cho vectơ $\vec{a} \neq \vec{0} .$ Chứng minh rằng $\frac{1}{|\vec{a}|} \vec{a}$ (hay còn được viết là $\frac{\vec{a}}{|\vec{a}|}$ ) là một vectơ đơn vị, cùng hướng với vectơ $\vec{a}$ .

Lời giải

Ta thấy $\frac{1}{|\vec{a}|} > 0 (\vec{a} \neq \vec{0})$ nên $\frac{1}{|\vec{a}|} \vec{a}$ là vectơ cùng hướng với vectơ $\vec{a} .$

Độ dài của vectơ $\frac{1}{|\vec{a}|} \vec{a}$ là: $|\frac{1}{|\vec{a}|} \vec{a}| = |\frac{1}{|\vec{a}|}| . |\vec{a}| = \frac{1}{|\vec{a}|} . |\vec{a}| = 1$

Vậy vectơ $\frac{1}{|\vec{a}|} \vec{a}$ (hay còn được viết là $\frac{\vec{a}}{|\vec{a}|}$ ) là một vectơ đơn vị, cùng hướng với vectơ $\vec{a}$ .

Bài 4.38 trang 72 Toán 10 Tập 1: Cho ba vectơ $\vec{a}, \vec{b}, \vec{u}$ với $|\vec{a}| = |\vec{b}| = 1$ và $\vec{a} ⊥ \vec{b}$ . Xét một hệ trục Oxy với các vectơ đơn vị $\vec{i} = \vec{a}, \vec{j} = \vec{b}$ . Chứng minh rằng:

a) Vectơ $\vec{u}$ có tọa độ là $(\vec{u} . \vec{a}; \vec{u} . \vec{b}) .$

b) $\vec{u} = (\vec{u} . \vec{a}) . \vec{a} + (\vec{u} . \vec{b}) . \vec{b} .$

Lời giải

Bài 4.39 trang 72 Toán 10 Tập 1: Trên sông, một ca nô chuyển động thẳng đều theo hướng S15°E (xem chú thích ở Bài 3.8, trang 42) với vận tốc có độ lớn bằng 20km/h. Tính vận tốc riêng của ca nô, biết rằng nước trên sông chảy về hướng đông với vận tốc có độ lớn bằng 3 km/h.

Lời giải

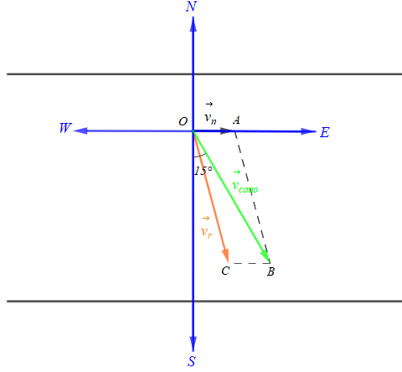
Ta mô tả bài toán bằng hình vẽ trên, trong đó:

$\vec{O E}$ là hướng đông, $\vec{OS}$ là hướng nam, $\vec{O W}$ là hướng tây, $\vec{O N}$ là hướng bắc;

$\vec{O A}$ biểu diễn vectơ vận tốc của dòng nước ${\vec{v}}_{n}$ và $O A = |{\vec{v}}_{n}| = 3$ ;

$\vec{O B}$ là hướng S15°E biểu diễn vectơ vận tốc chuyển động của ca nô ${\vec{v}}_{c a n o}$ tạo với $\vec{O S}$ một góc 15° và $O B = |{\vec{v}}_{c a n o}| = 20$ ;