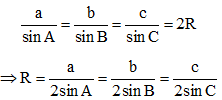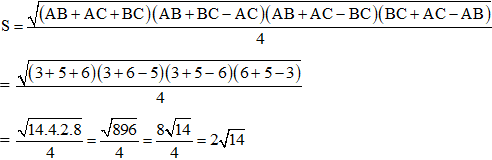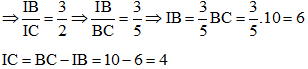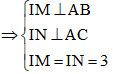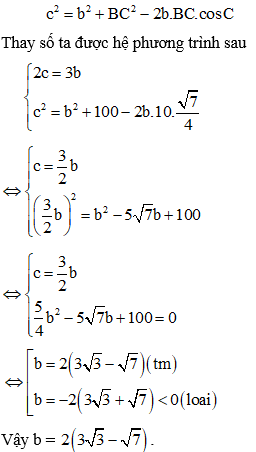Công thức tính bán kính đường tròn ngoại tiếp và bài tập vận dụng

Cô Nguyễn Thanh Phương 02/06/2023

Mời các em theo dõi nội dung bài học về Công thức tính bán kính đường tròn ngoại tiếp và bài tập vận dụng do thầy cô trường THCS Bình Chánh biên soạn. Hy vọng sẽ là tài liệu hữu ích giúp các em học tốt và hoàn thành tốt bài tập của mình.

Mục lục

Công thức tính bán kính đường tròn ngoại tiếp

Cho tam giác ABC có AB = c, AC = b, BC = a, R là bán kính đường tròn ngoại tiếp tam giác ABC, S là diện tích tam giác ABC

Cách 1: Sử dụng công thức diện tích tam giác

$S = \frac{{abc}}{{4R}} \Rightarrow R = \frac{{abc}}{{4S}}$

Bạn đang xem: Công thức tính bán kính đường tròn ngoại tiếp và bài tập vận dụng

Cách 2: Sử dụng định lí Sin trong tam giác

Ta có:

$\begin{matrix} \dfrac{a}{{\sin \widehat A}} = \dfrac{b}{{\sin \widehat B}} = \dfrac{c}{{\sin \widehat C}} = 2R \hfill \\ \Rightarrow R = \dfrac{a}{{2\sin \widehat A}} = \dfrac{b}{{2\sin \widehat B}} = \dfrac{c}{{2\sin \widehat C}} \hfill \\ \end{matrix}$

Cách 3: Tính chất của tam giác vuông

– Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền, do đó bán kính đường tròn ngoại tiếp tam giác vuông chính bằng nửa độ dài cạnh huyền.

Cách 4: Sử dụng hệ tọa độ

– Tìm tọa độ tâm O của đường tròn ngoại tiếp tam giác ABC

– Tìm tọa độ một trong ba đỉnh A, B, C (nếu chưa có)

– Tính khoảng cách từ tâm O tới một trong ba đỉnh A, B, C, đây chính là bán kính cần tìm: R = OA = OB = OC

Phương pháp giải

Phương pháp 1: Sử dụng đinh lý sin trong tam giác

Cho tam giác ABC có BC = a, CA = b và AB = c, R là bán kính đường tròn ngoại tiếp tam giác ABC. Khi đó:

Phương pháp 2: Sử dụng diện tích tam giác

Phương pháp 3: Sử dụng trong hệ tọa độ

– Tìm tọa độ tâm O của đường tròn ngoại tiếp tam giác ABC

– Tìm tọa độ một trong ba đỉnh A, B, C (nếu chưa có)

– Tính khoảng cách từ tâm O tới một trong ba đỉnh A, B, C, đây chính là bán kính cần tìm R = OA = OB = OC.

Phương pháp 4: Sử dụng trong tam giác vuông

Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền, do đó bán kính đường tròn ngoại tiếp tam giác vuông chính bằng nửa độ dài cạnh huyền.

Bài tập vận dụng tính bán kính đường tròn ngoại tiếp tam giác

Ví dụ 1: Cho tam giác ABC có góc B bằng 45° và AC = 4. Tính bán kính đường tròn ngoại tiếp tam giác ABC.

Hướng dẫn giải:

Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC.

Ta có: b = AC = 4

Áp dụng định lý sin trong tam giác ABC ta có:

Ví dụ 2: Cho tam giác ABC có AB = 3, AC = 5 và BC = 6. Tính bán kính đường tròn ngoại tiếp tam giác ABC.

Hướng dẫn giải:

Theo công thức Hê – rông, diện tích tam giác ABC là:

Bán kính đường tròn ngoại tiếp tam giác ABC là:

Ví dụ 3: Cho tam giác MNP có MN = 6, MP = 8 và PN = 10. Tính bán kính đường tròn ngoại tiếp tam giác MNP.

Hướng dẫn giải:

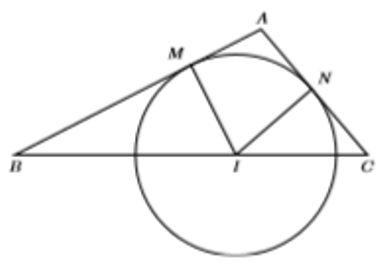
Ví dụ 4: Cho tam giác ABC có BC = 10. Gọi (I) là đường tròn có tâm I thuộc cạnh BC và tiếp xúc với các cạnh AB, AC lần lượt tại M và N. Biết đường tròn (I) có bán kính bằng 3 và 2IB = 3IC. Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.

Hướng dẫn giải:

+ Vì 2IB = 3IC

+ Vì M và N lần lượt là tiếp điểm của đường tròn tâm I với AB và AC

+ Mặt khác theo định lý Cô – sin trong tam giác ABC ta có:

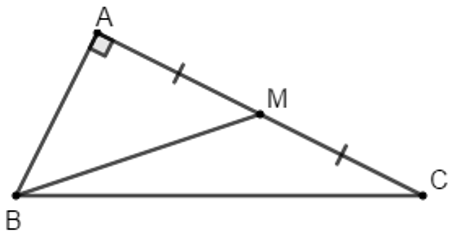
Ví dụ 5: Cho tam giác ABC vuông tại A có AB = 1; AC = 4. Gọi M là trung điểm AC.

a) Tính diện tích tam giác ABC.

b) Tính bán kính R₁ của đường tròn ngoại tiếp tam giác ABC.

c) Tính bán kính R₂ của đường tròn ngoại tiếp tam giác CBM.

Hướng dẫn giải:

a) Tam giác ABC vuông tại A, nên diện tích tam giác ABC là:

b) Tam giác ABC vuông tại A, theo định lý Pytago ta có

BM² = AB² + AM² = 1² + 2² = 5 (tam giác AMB vuông tại A)

Bán kính đường tròn ngoại tiếp tam giác CMB là:

***

Trên đây là nội dung bài học Công thức tính bán kính đường tròn ngoại tiếp và bài tập vận dụng do thầy cô trường THCS Bình Chánh biên soạn và tổng hợp. Hy vọng sẽ giúp các em hiểu rõ nội dung bài học và từ đó hoàn thành tốt bài tập của mình. Đồng thời luôn đạt điểm cao trong các bài thi bài kiểm tra sắp tới. Chúc các em học tập thật tốt.

Đăng bởi THCS Bình Chánh trong chuyên mục Học tập