Công thức tính diện tích tam giác và bài tập vận dụng

Cô Nguyễn Thanh Phương 28/05/2023

Mời các em theo dõi nội dung bài học về Công thức tính diện tích tam giác và bài tập vận dụng do thầy cô trường THCS Bình Chánh biên soạn. Hy vọng sẽ là tài liệu hữu ích giúp các em học tốt và hoàn thành tốt bài tập của mình.

Mục lục

Công thức tính diện tích hình tam giác

Với hình tam giác thì tùy vào từng hình sẽ có công thức khác nhau được sử dụng.

Tính diện tích tam giác thường

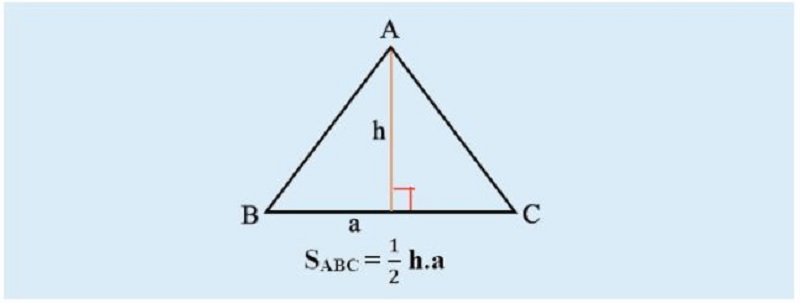
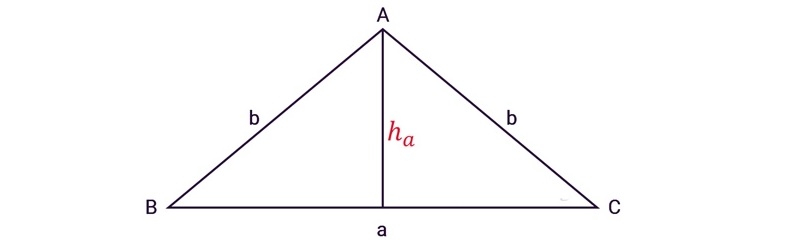
Đối với tam giác thường ABC có 3 cạnh a, b, c và ha là đường cao thuộc đỉnh a. Ta có:

Bạn đang xem: Công thức tính diện tích tam giác và bài tập vận dụng

Diện tích tam giác bằng ½ tích của chiều cao hạ từ đỉnh với độ dài cạnh đối diện của đỉnh đó.

S = (a x h)/2

Công thức suy ra:

h = (S x 2) / a hoặc a = (S x 2) / h

Ví dụ:

Tính diện tích hình tam giác có độ dài đáy là 5m và chiều cao là 24dm.

Giải: Chiều cao 24dm = 2,4m

Diện tích tam giác là

S=(5 x 2.4)/2 = 6m2

Tính diện tích tam giác cân

Tam giác cân là tam giác có 2 cạnh bằng nhau. Diện tích tam giác cân bằng tích của chiều cao nối từ đỉnh tam giác đó tới cạnh đáy tam giác, sau đó chia cho 2.

Công thức tính diện tích tam giác cân:

S = (a x h)/ 2

a: Chiều dài đáy tam giác cân (đáy là một trong 3 cạnh của tam giác)
h: Chiều cao của tam giác (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy).

Ví dụ: Tính diện tích của tam giác cân có:

a, Độ dài cạnh đáy bằng 6cm và đường cao bằng 7cm

b, Độ dài cạnh đáy bằng 5m và đường cao bằng 3,2m

Lời giải:

a, Diện tích của hình tam giác là:

(6 x 7) : 2 = 21 (cm2)

Đáp số: 21cm2

b, Diện tích của hình tam giác là:

(5 x 3,2) : 2 = 8 (m2)

Đáp số: 8m2

Tính diện tích tam giác đều

Tam giác đều là tam giác có 3 cạnh bằng nhau. Trong đó, cách tính diện tích của tam giác đều cũng sẽ như các tính tam giác thường, khi ta chỉ cần biết cạnh đáy và chiều cao tam giác.

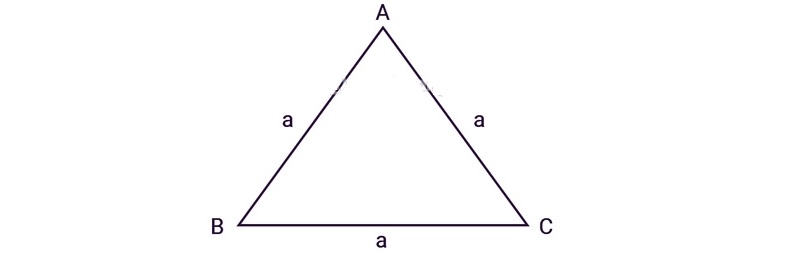
Vậy nên, diện tích tam giác đều sẽ bằng tích của chiều cao với cạnh đáy, sau đó chia cho 2.

Công thức tính diện tích tam giác đều:

S = (a x h)/ 2

a: Chiều dài đáy tam giác đều (đáy là một trong 3 cạnh của tam giác)
h: Chiều cao của tam giác (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy).

Ví du: Tính diện tích của tam giác đều có:

a, Độ dài một cạnh tam giác bằng 6cm và đường cao bằng 10cm

b, Độ dài một cạnh tam giác bằng 4cm và đường cao bằng 5cm

Lời giải

a, Diện tích hình tam giác là:

(6 x 10) : 2 = 30 (cm2)

Đáp số: 30cm2

b, Diện tích hình tam giác là:

(4 x 5) : 2 = 10 (cm2)

Đáp số: 10cm2

Tính diện tích tam giác vuông

Tam giác vuông là tam giác có 1 góc vuông 90 °. Về cách tính diện tích của tam giác vuông cũng sẽ bằng ½ tích của chiều cao với chiều dài đáy. Nhưng với loại tam giác này sẽ có chút khác biệt hơn vì thể hiện rõ chiều dài đáy và chiều cao, nên bạn không cần phải vẽ thêm để tính chiều cao của hình.

Công thức tính diện tích tam giác vuông: S = (a X h) / 2

Nhưng vì tam giác vuông có 2 cạnh góc vuông, nên chiều cao sẽ ứng với 1 cạnh góc vuông, cùng với chiều dài đáy sẽ ứng với cạnh góc vuông còn lại.

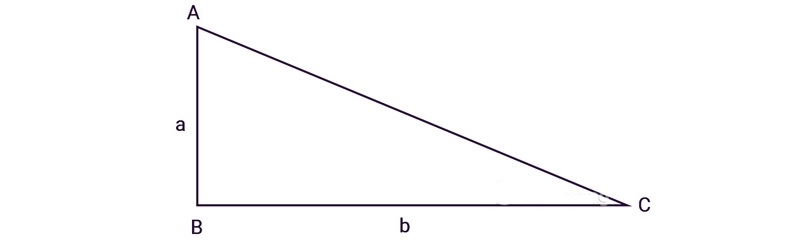
Từ đó, ta có công thức tính diện tích tam giác vuông:

S = (a x b)/ 2

Trong đó a, b: độ dài hai cạnh góc vuông

Công thức suy ra:

a = (S x 2) : b hoặc b = (S x 2) : a

Ví dụ: Tính diện tích của tam giác vuông có:

a, Hai cạnh góc vuông lần lượt là 3cm và 4cm

b, Hai cạnh góc vuông lần lượt là 6m và 8m

Lời giải:

a, Diện tích của hình tam giác là:

(3 x 4) : 2 = 6 (cm2)

Đáp số: 6cm2

b, Diện tích của hình tam giác là:

(6 x 8) : 2 = 24 (m2)

Đáp số: 24m2

Tính diện tích tam giác vuông cân

Tam giác vuông cân là tam giác vừa vuông, vừa cân. Như hình vẽ, cho tam giác ABC vuông cân tại A, a là độ dài hai cạnh góc vuông.

Dựa vào công thức tính tam giác vuông cho tam giác vuông cân, với chiều cao và cạnh đáy bằng nhau. Ta có công thức:

S = 1/2 x a2

Tính diện tích tam giác trong hệ tọa độ Oxyz

Trên lý thuyết, ta có thể dùng các công thức tính tam giác phẳng cho tam giác trong không gian Oxyz. Nhưng như vậy sẽ gặp nhiều khó khăn khi tính toán. Vậy nên, trong không gian Oxyz, ta sẽ tính diện tích tam giác dựa vào tích có hướng.

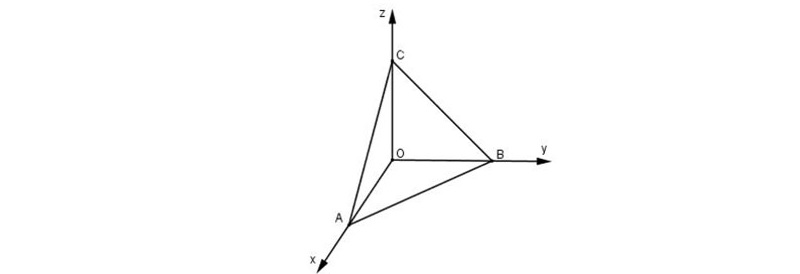
Trong không gian Oxyz, cho tam giác ABC. Diện tích tam giác ABC được tính theo công thức:

Ví dụ minh họa:

Trong không gian Oxyz, cho tam giác ABC có tọa độ ba đỉnh lần lượt là A(-1;1;2), B(1;2;3), C(3;-2;0). Tính diện tích tam giác ABC.

Bài giải:

Các dạng bài tập tính diện tích hình tam giác

Đối với kiến thức về hình tam giác, tùy vào mỗi cấp học sẽ có những dạng bài tập riêng. Nhưng với các bé đang trong độ tuổi cấp 1, sẽ thường gặp những dạng bài tập tính diện tích của hình tam giác như sau:

Dạng 1: Tính diện tích tam giác khi biết độ dài đáy và chiều cao

Đối với dạng bài tập này, đề bài thường sẽ cho dữ kiện về chiều cao và độ dài cạnh đáy. Nên các em chỉ cần áp dụng công thức tính tam giác thường để tìm ra đáp án chính xác.

Ví dụ: Tính diện tích tam giác thường và tam giác vuông có:

a) Độ dài đáy bằng 32cm và chiều cao bằng 25cm.

b) Hai cạnh góc vuông có độ dài lần lượt là 3dm và 4dm.

Lời giải:

a) Diện tích hình tam giác là:

32 x 25 : 2 = 400 (cm2)

b) Diện tích hình tam giác là:

3 x 4 : 2 = 6 (dm2)

Đáp số: a) 400cm2; b) 6dm2

Dạng 2: Tính độ dài đáy khi biết diện tích và chiều cao

Ở dạng bài tập này, dữ kiện đề bài sẽ cho biết thông số của chiều cao và diện tích hình tam giác, yêu cầu học sinh sẽ tính độ dài đáy. Nên từ công thức tính diện tích, ta suy ra công thức tính độ dài đáy: a = S x 2 : h

Ví dụ: Cho hình tam giác với diện tích bằng 4800cm2, chiều cao là 80cm. Tính độ dài cạnh đáy bằng bao nhiêu?

Lời giải:

Độ dài cạnh đáy của hình tam giác là:

4800 x 2 : 80 = 120 (cm)

Đáp số: 120cm

Dạng 3: Tính chiều cao khi biết diện tích và độ dài đáy

Cũng từ công thức tính diện tích của hình tam giác, ta cũng sẽ suy ra công thức tính chiều cao của hình như sau: h = S x 2 : a

Ví dụ: Cho hình tam giác, biết diện tích bằng 1125cm2, độ dài đáy bằng 50cm, tính chiều cao của hình tam giác đó.

Lời giải:

Chiều cao của hình tam giác là:

1125 x 2 : 50 = 45 (cm)

Đáp số: 45cm

Bài tập vận dụng

Bài 1: Một hình tam giác có đáy 15 cm và chiều cao 2,4cm. Tính diện tích hình tam giác đó?

Giải:

Diện tích hình tam giác là:

15 x 2,4 : 2 = 18 (cm2)

Đáp số: 18cm2

Bài 2: Một hình tam giác có đáy 12cm và chiều cao 25mm. Tính diện tích hình tam giác đó?

Giải:

Đổi: 25mm = 2,5 cm

Diện tích hình tam giác đó là:

12 x 2,5 : 2 = 15 (cm2)

Đáp số: 15cm2

Bài 3: Một lăng tẩm hình tam giác có diện tích 129m2, chiều cao 24m. Hỏi cạnh đáy của tam giác đó là bao nhiêu?

Giải:

Cạnh đáy của tam giác đó là:

129 x 2 : 24 = 10,75 (m)

Đáp số: 10,75m

Bài 4: Một tấm bảng quảng cáo hình tam giác có tổng cạnh đáy và chiều cao là 28m, cạnh đáy hơn chiều cao 12m. Tính diện tích tấm bảng quảng cáo đó ?

Giải:

Độ dài cạnh đáy là:

(28 + 12) : 2 = 20 (m)

Độ dài chiều cao là:

28 – 20 = 8 (m)

Diện tích tấm bảng quảng cáo là:

20 x 8 : 2 = 80 (m2)

Đáp số: 80m2

Bài 5: Một hình chữ nhật có diện tích 630cm2 và diện tích này bằng 70% diện tích hình tam giác. Tính cạnh đáy hình tam giác, biết chiều cao là 2,4dm ?

Giải:

Đổi: 2,4dm = 24cm

Diện tích hình tam giác là:

630 : 70% = 900 (cm2)

Cạnh đáy hình tam giác là:

900 x 2 : 24 = 75 (cm)

Đáp số: 75cm

Bài 6: Một tấm bìa hình chữ nhật có diện tích 60464mm2 và diện tích này bằng 4/3 diện tích tấm bìa hình tam giác. Tính cạnh đáy tấm bìa hình tam giác, biết chiều cao tấm bìa là 24cm ?

Giải:

Đổi 24cm = 240mm

Diện tích hình tam giác là:

60464 : 4/3 = 45348 (mm2)

Cạnh đáy tấm bìa hình tam giác là:

45348 x 2 : 240 = 377,9 (mm)

Đáp số: 377,9mm

Bài 7: Cho tam giác ABC vuông góc tại B, chu vi là 37dm. Cạnh AB bằng 2/3 cạnh AC, cạnh BC bằng 4/5 cạnh AC. Tính diện tích hình tam giác ABC ?

Giải:

Ta có:

Cạnh AC là 15 phần bằng nhau thì cạnh AB là 10 phần và BC là 12 phần như thế.

Độ dài cạnh AB là:

37 : (15 + 10 + 12) x 10 = 10 (dm)

Độ dài cạnh AC là:

37 : (15 + 10 + 12) x 15 = 15 (dm)

Độ dài cạnh BC là:

37 – 10 – 15 = 12 (dm)

Diện tích hình tam giác ABC là:

10 x 12 : 2 = 60 (dm2)

Đáp số: 60dm2

Bài 8: Cho tam giác ABC vuông góc tại A, chu vi là 90cm. Cạnh AB bằng 4/3 cạnh AC, cạnh BC bằng 5/3 cạnh AC. Tính diện tích hình tam giác ABC ?

Giải:

Cạnh AC là 3 phần bằng nhau thì cạnh AB là 4 phần và cạnh BC là 5 phần như thế

Độ dài cạnh AB là:

90 : (3 + 4 + 5) x 4 = 30 (cm)

Độ dài cạnh AC là:

90 : (3 + 4 + 5) x 3 = 22,5 (cm)

Diện tích hình tam giác ABC là:

30 x 22,5 : 2 = 337,5 (cm2)

Đáp số: 337,5 cm2

Bài 9: Một thửa đất hình tam giác có chiều cao là 10 m. Hỏi nếu kéo dài đáy thêm 4 m thì diện tích sẽ tăng thêm bao nhiêu m2?

Giải:

Nếu kéo dài đáy thêm 4m thì diện tích sẽ tăng thêm là:

10 x 4 : 2 = 20 (m2)

Đáp số: 20m2

Bài 10: Một hình tam giác ABC có cạnh đáy 3,5m. Nếu kéo dài cạnh đáy BC thêm 2,7m thì diện tích tam giác tăng thêm 5,265 m2. Tính diện tích hình tam giác ABC đó ?

Giải:

Độ dài chiều cao của hình tam giác là:

5,265 x 2 : 2,7 = 3,9 (m)

Diện tích hình tam giác ABC là:

3,5 x 3,9 : 2 = 6,825 (m2)

Đáp số: 6,825 m2

Bài 11: Tính diện tích hình tam giác có:

a) Độ dài đáy là 32cm và chiều cao là 22cm;

b) Độ dài đáy là 2,5 cm và chiều cao là 1,2cm;

Giải:

a) S = 1/2 x 32 x 22 = 352 cm2

b) S = 1/2 x 2,5 x 1,2 = 1,5 cm2

Bài 12: Tính diện tích hình tam giác có:

a) Độ dài đáy là 45cm và chiều cao là 2,4dm;

b) Độ dài đáy là 1,5 m và chiều cao là 10,2dm;

Giải:

a) Đổi 2,4 dm = 24cm

S = 1/2 x 45 x 2,4 = 540cm2

b) Đổi 10,2dm = 1,02m

S = 1/2 x 1,02 x 1,5m = 0,765m2

Bài 13: Tính diện tích hình tam giác có:

a) Độ dài đáy là 3/4m và chiều cao là 1/2m;

b) Độ dài đáy là 4/5 m và chiều cao là 3,5 dm;

Giải:

a) S = 1/2 x 3/4 x 1/2 = 3/16m2

b) Đổi 4/5m = 40/5dm = 8dm2

S = 1/2 x 8 x 3,5 = 14dm2

Bài 14: Tính diện tích hình tam giác vuông có độ dài 2 cạnh góc vuông lần lượt là:

a) 35cm và 15 cm.

b) 3,5 m và 15 dm.

Giải:

a) S = 1/2 x 35 x 15 = 262,5cm2

b) S = 1/2 x 35 x 15 = 262,5 dm2 (đổi 3,5m = 35 dm)

Bài 15:

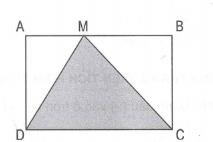
Tính diện tích hình tam giác MDC. Biết hình chữ nhật ABCD có AB = 25 cm, BC = 16cm.

Giải:

Hình tam giác MDC có chiều cao MH bằng với chiều rộng hình chữ nhật ABCD. Vì thế diện tích MDC bằng 1/2 x 25 x 16 = 200cm2

Bài 16:

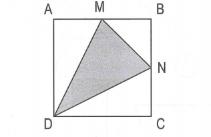
Tính diện tích hình tam giác MDN. Biết hình vuông ABCD có cạnh 20cm và AM = MB , BN = NC.

Giải:

Muốn tính diện tích hình tam giác MDN ta lấy diện tích hình vuông ABCD trừ đi tổng diện tích của ba hình tam giác vuông DAM, MBN và NCD

Ta có:

AM = MB = BN = NC = 20 : 2 = 10 (cm)

Diện tích hình tam giác DAM là:

20 x 10 : 2 = 100 ( cm2)

Diện tích hình tam giác MBN là:

10 x 10 : 2 = 50 (cm2)

Diện tích hình tam giác NCD là:

10 x 10 : 2 = 100 (cm2)

Diện tích hình vuông ABCD là:

20x 20 = 400 (cm2)

Vậy diện tích tam giác MDN là:

400 – (100 + 50 +1 00) = 150 (cm2)

Bài 17: Tính độ dài cạnh đáy của hình tam giác có chiều cao là 2/5m và diện tích là 1200 cm2

Giải:

Độ dài đáy của tam giác là 2 x 0,12 : 2/5 = 0,6m (đổi 1200 cm2 = 0,12m2)

Bài 18:

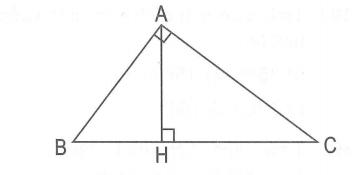
Tính chiều cao AH của hình tam giác vuông ABC. Biết: AB = 30 cm ; AC = 40 cm ; BC = 50 cm.

Giải:

Ta thấy BC là cạnh huyền do đó, ABC là tam giác vuông tại A.

Diện tích tam giác ABC là 1/2 x AB x AC = 1/2 x 30 x 40 = 600cm2

Chiều cao AH của hình tam giác ABC là 2 x 600 : BC = 2 x 600 : 50 = 24cm

Bài 19: Cho tam giác ABC có diện tích 150cm2. M là trung điểm của BC, N là trung điểm của AC. Nối MN. Tính diện tích tam giác CMN ?

Bài giải:

Ta có: SABC = 2 x SAMC (chung chiều cao hạ từ A xuống đáy BC và đáy BC = 2 x MC)

Từ đó ta có: SAMC = 150 : 2 = 75 (cm2)

Ta có:SAMC = 2 x SCMN (chung chiều cao hạ từ M xuống đáy AC và đáy AC = 2 x NC)

Từ đó ta có: SCMN = 75 : 2 = 37,5 (cm2)

Đáp số: 37,5 cm2

Bài 20:

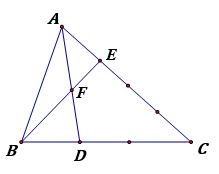
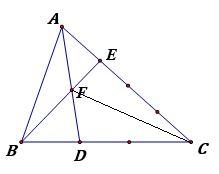
Cho hình vẽ. Tính tỉ số diện tích 2 tam giác BDF và AEF ?

Bài giải:

Ta có: AE = 1/3 x EC nên SABF=1/3xSBFC

BD = 1/3 x BC nên SBDF=13xSBFC

Vậy SABF=SBDF (1)

Ta có: DC = 2 x BD nên SACF=2xSABF

EC = 4 x AE nên SACF=4xSAEF

Vậy 4xSAEF=2xSABF hay 2xSAEF=SABF (2)

Từ (1) và (2): SABF=2xSAEF

Vậy tỉ số là 2

***

Trên đây là nội dung bài học Công thức tính diện tích tam giác và bài tập vận dụng do thầy cô trường THCS Bình Chánh biên soạn và tổng hợp. Hy vọng sẽ giúp các em hiểu rõ nội dung bài học và từ đó hoàn thành tốt bài tập của mình. Đồng thời luôn đạt điểm cao trong các bài thi bài kiểm tra sắp tới. Chúc các em học tập thật tốt.

Đăng bởi THCS Bình Chánh trong chuyên mục Học tập