Học Tập Lớp 10 Tin học 10 Kết nối tri thức

Giải Vận dụng trang 30 Toán 10 tập 1 SGK Kết nối tri thức với cuộc sống

Trường THCS Bình Chánh 02/10/2023

Mời các em theo dõi nội dung bài học do thầy cô trường THCS Bình Chánh biên soạn sẽ giúp các em nắm chắc kiến thức nội dung bài học tốt hơn.

Mục lục

Vận dụng trang 30 SGK Toán 10

Toán lớp 10 Vận dụng trang 30 là lời giải bài Hệ bất phương trình bậc nhất hai ẩn SGK Toán 10 sách Kết nối tri thức với cuộc sống hướng dẫn chi tiết lời giải giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 10. Mời các em học sinh cùng tham khảo chi tiết.

Giải Vận dụng Toán 10 trang 30

Vận dụng (SGK trang 30): Một cửa hàng có kế hoạch nhập về hai loại máy tính A và B, giá mỗi chiếc lần lượt là 10 triệu đồng và 20 triệu đồng với số vốn ban đầu không vượt quá 4 tỉ đồng. Loại máy A mang lại lợi nhuận 2,5 triệu đồng cho mỗi máy bán được và loại máy B mang lại lợi nhuận là 4 triệu đồng mỗi máy. Cửa hàng ước tính rằng tổng nhu cầu hàng tháng sẽ không vượt quá 250 máy. Giả sử trong một tháng cửa hàng cần nhập số máy tính loại A là x và số máy tính loại B là y.

Bạn đang xem: Giải Vận dụng trang 30 Toán 10 tập 1 SGK Kết nối tri thức với cuộc sống

a) Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình rồi xác định miền nghiệm của hệ đó.

b) Gọi F (triệu đồng) là lợi nhuận mà cửa hàng thu được trong tháng đó khi bán x máy tính loại A và y máy tính loại B. Hãy biểu diễn F theo x và y.

c) Tìm số lượng máy tính mỗi loại cửa hàng cần nhập về trong tháng đó để lợi nhuận thu được là lớn nhất.

Hướng dẫn giải

– Trong mặt phẳng tọa độ, tập hợp các điểm có tọa độ là nghiệm của hệ bất phương trình bậc nhất hai ẩn là miền nghiệm của hệ bất phương trình đó.

– Miền nghiệm của hệ là giao các miền nghiệm của các bất phương trình trong hệ.

– Cách xác định miền nghiệm của một hệ bất phương trình bậc nhất hai ẩn:

+ Trên cùng một mặt phẳng tọa độ, xác định miền nghiệm của mỗi bất phương trình bậc nhất hai ẩn trong hệ và gạch bỏ miền còn lại.

+ Miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho.

Lời giải chi tiết

a) Số máy tính loại A cửa hàng cần nhập trong một tháng là x (máy), số máy tính loại B cửa hàng cần nhập trong một tháng là y (máy) (x,y ≥ 0).

Do tổng nhu cầu hàng tháng sẽ không vượt quá 250 máy: x + y ≤ 250

Tổng số vốn cửa hàng cần nhập hai loại A và B: 10x + 20y (triệu đồng)

Vì số vốn ban đầu không vượt quá 4 tỉ đồng nên ta có: 10x + 20y ≤ 4 000

Khi đó ta có hệ bất phương trình: $\left\{ {\begin{array}{*{20}{c}} {x \geqslant 0} \\ {y \geqslant 0} \\ {x + y \leqslant 250} \\ {10x + 20y \leqslant 4000} \end{array}} \right.$

Miền nghiệm D₃ của bất phương trình x + y ≤ 250 và gach bỏ miền còn lại

– Vẽ đường thẳng d: x + y – 250 = 0.

– Vì 0 + 0 = 0 < 250 nên tọa độ điểm O(0;0) thỏa mãn bất phương trình x + y ≤ 250

Do đó miền nghiệm D₃của bất phương trình x + y ≤ 250 là nửa mặt phẳng bờ d chứa gốc tọa độ.

Miền nghiệm D₄ của bất phương trình 10x + 20y ≤ 4 000 và gach bỏ miền còn lại

– Vẽ đường thẳng d’: 10x + 20y – 4 000 = 0.

– Vì 10.0 + 20.0 = 0 < 4 000 nên tọa độ điểm O(0;0) thỏa mãn bất phương trình 10x + 20y < 4 000

Do đó miền nghiệm D₄của bất phương trình 10x + 20y < 4 000 là nửa mặt phẳng bờ d’ chứa gốc tọa độ.

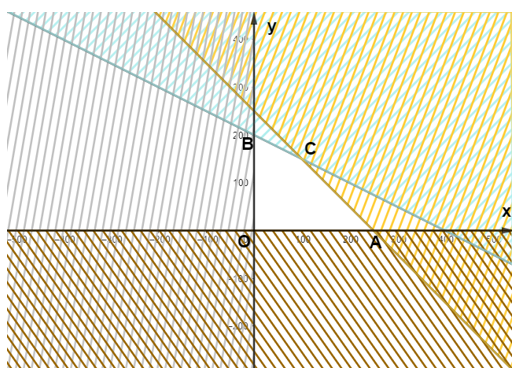
Miền nghiệm của hệ bất phương trình là tứ giác OACB với O(0;0), A(250;0), C(100;150), B(0; 200)

b) Lợi nhuận mà cửa hàng thu được trong tháng đó khi bán x máy tính loại A và y máy tính loại B là: F(x;y) = 2,5x + 4y (triệu đồng).

Vậy F(x;y) = 2x + 4y.

c) Bài toán chuyển về tìm giá trị lớn nhất của F(x;y) với (x;y) thuộc miền nghiệm của hệ bất phương trình $\left\{ {\begin{array}{*{20}{c}} {x \geqslant 0} \\ {y \geqslant 0} \\ {x + y \leqslant 250} \\ {10x + 20y \leqslant 4000} \end{array}} \right.$

Tại O(0;0): F(0;0) = 2,5.0 + 4.0 = 0;

Tại A(250;0): F(250;0) = 2,5.250 + 4.0 = 625;

Tại C(100;150): F(100;150) = 2,5.100 + 4.150 = 850;

Tại B(0;200): F(0;200) = 2,5.0 + 4.200 = 800.

Do đó F(x;y) lớn nhất bằng 850 với x = 100 và y = 150.

Vậy cửa hàng cần nhập 100 máy loại A, 150 máy loại B để cửa hàng thu được lợi nhuận lớn nhất là 850 triệu đồng.

—–> Câu hỏi cùng bài:

Luyện tập 2 (SGK trang 28): Biểu diễn miền nghiệm của hệ bất phương trình …
Hoạt động 3 (SGK trang 28): Xét biểu thức F(x; y) = 2x+ 3y với (x; y) …
Bài 2.4 (SGK trang 30): Hệ bất phương trình nào sau đây là hệ bất phương trình …
Bài 2.5 (SGK trang 30): Biểu diễn miền nghiệm của mỗi hệ bất phương trình …

—> Bài liên quan: Giải Toán 10 Bài 4 Hệ bất phương trình bậc nhất hai ẩn

—-> Bài học tiếp theo: Giải Toán lớp 10 Bài tập cuối chương 2 trang 31

—————————————-

Trên đây là lời giải chi tiết Vận dụng Toán lớp 10 trang 30 Bài 4 Hệ bất phương trình bậc nhất hai ẩn cho các em học sinh tham khảo, nắm được cách giải các dạng toán của Chương 2: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn. Hi vọng đây là tài liệu hữu ích cho các bạn ôn tập kiểm tra năng lực, bổ trợ cho quá trình học tập trong chương trình THPT cũng như ôn luyện cho kì thi THPT Quốc gia. Chúc các bạn học tốt!

Ngoài ra mời bạn đọc tham khảo thêm một số tài liệu: Giải Toán 10 sách CTST, Giải Toán 10 sách Cánh Diều, Hỏi đáp Toán 10

Đăng bởi: THCS Bình Chánh

Chuyên mục: Toán 10 Kết nối tri thức