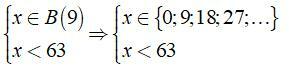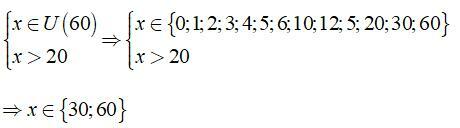Ước số là gì? Bội số là gì? Cách tìm ước và bội

Cô Nguyễn Thanh Phương 28/09/2023

Mời các em theo dõi nội dung bài học về Ước số là gì? Bội số là gì? Cách tìm ước và bội do thầy cô trường THCS Bình Chánh biên soạn. Hy vọng sẽ là tài liệu hữu ích giúp các em học tốt và hoàn thành tốt bài tập của mình.

Mục lục

Ước số là gì?

Số nguyên dương b lớn nhất là ước của cả hai số nguyên a, b được gọi là ước số chung lớn nhất (ƯCLN) của a và b. Trong trường hợp cả hai số nguyên a và b đều bằng 0 thì chúng không có ƯCLN vì khi đó mọi số tự nhiên khác không đều là ước chung của a và b.

Nói theo cách khác uớc số là một số tự nhiên khi một số tự nhiên khác chia với nó sẽ được chia hết.

Bạn đang xem: Ước số là gì? Bội số là gì? Cách tìm ước và bội

Mô tả rõ hơn thì khi một số tự nhiên A được gọi là ước số của số tự nhiên B nếu B chia hết cho A.

Ví dụ: 6 chia hết được cho [1,2,3,6], thì [1,2,3,6] được gọi là ước số của 6.

Ước chung lớn nhất là gì?

Ước số chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp ước chung.

Cách tìm ước chung lớn nhất (ƯCLN)

Bước 1: Phân tích mỗi số ra thừa số nguyên tố.

Bước 2: Chọn ra các thừa số nguyên tố chung.

Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó. Tích đó là UCLN cần tìm.

Chú ý:

Hai số nguyên tố cùng nhau khi và chỉ khi ước chung lớn nhất của hai số bằng 1.
Cách tìm Ước chung thông qua tìm UCLN.

Bội số là gì?

Bội số của A là các số chia hết cho A

Bối số nhỏ nhất của A là số nhỏ nhất chia hết cho A

Ví dụ: bội số của 3 là 3, 6, 9, 12, 15 …

Bội số nhỏ nhất của 3 là chính nó.

Bội số chung nhỏ nhất là gì?

Bội chung nhỏ nhất của hai hay nhiều số là số nhỏ nhất khác 0 trong tập hợp bội chung.

Cách tìm bội số chung nhỏ nhất

Bước 1: Phân tích mỗi số ra thừa số nguyên tố.

Bước 2: Chọn ra các thừa số nguyên tố chung và riêng.

Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN cần tìm.

Chú ý:

Nếu hai số a, b là hai số nguyên tố cùng nhau thì BCNN là tích của a.b
Nếu a là bội của b thì a cũng chính là BCNN của hai số a, b.

Cách tìm ước và bội

– Muốn tìm bội của một số tự nhiên khác 0, ta nhân số đó với các số tự nhiên 0; 1; 2; 3….

– Muốn tìm ước cả một số tự nhiên a (a>1), ta chia số a cho các số tự nhiên từ 1 đến a để xét xem a có thể chia hết cho số nào; khi đó các số ấy là ước của a

Ví dụ: Tìm các bội nhỏ hơn 50 của 9

Ta lần lượt nhân 9 với 0; 1; 2; 3; 4; 5; 6 ta dược các bội nhỏ hơn 50 của 9 là 0; 9; 18; 27; 36; 45 (bội tiếp theo của 9 là 54 lớn hơn 50)

Ví dụ: Tìm tập hợp các ước của 9

Lần lượt chia 9 cho 1; 2; 3; 4; 5; 6; 7; 8; 9 ta thấy 9 chỉ chia hết cho 1; 3; 9 nên:

Ư (9) = {1; 3; 9}

Hợp số là gì?

Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn hai ước.

Lưu ý: Số 0 và 1 không là số nguyên tố và cũng không là Hợp số.

Các dạng bài tập về ước và bội

Dạng 1. Nhận biết một số là ước, bội của một số cho trước

Phương pháp giải:

– Để xét a có là ước của một số cho trước hay không, ta chia số đó cho a. Nếu chia hết thì a là ước của số đó

– Để xét b có là bội của một số khác 0 hay không, ta chia b cho số đó. Nếu chia hết thì b là bội của số đó.

Bài 1. Cho các số sau 0; 1; 3; 14; 7; 10; 12; 5; 20. Tìm các số

a. Là Ước của 6

b. Là ước của 10

Đáp án

a. Vì trong các số đã cho 6 chia hết cho 1 và 3 nên Ư (6) = {1; 3}

b. Vì trong các số đã cho 10 chia hết cho 1; 5; 10 nên Ư (10) = {1; 5; 10}

Bài 2. Cho các số sau 13; 19; 20; 36; 121; 125; 201; 205; 206 chỉ ra các số thuộc tập hợp sau:

a. là bội của 3

b. Là bội của 5

Đáp án

a. Vì trong các số đã cho 36; 201 chia hết cho 3 nên B (3) = {36; 201}

b. Vì trong các số đã cho 20; 125; 205 chia hết cho 5 nên B (5) = {20; 125; 205}

Dạng 2. Tìm tất cả các ước, bội của một số

Phương pháp giải:

– Để tìm tất cả các ước của một số a ta làm như sau:

Bước 1: Chia a lần lượt cho các số 1; 2; 3; 4; …;a
Bước 2: Liệt kê các số mà a chia hết. Đó là tất cả các ước của a

– Để tìm bội của một số b (b#0) ta làm như sau:

Bước 1: Nhân b lần lượt với các số 0; 1; 2; 3; ….
Bước 2: Liệt kê các số thu được. Đó là tất cả các bội của b

* Lưu ý: Nếu bài toán tìm ước và bội của một số thỏa mãn điều kiện cho trước, ta làm như sau:

Bước 1: Liệt kê các ước, bội của số đó
Bước 2: Chọn ra các số thỏa mãn điều kiện đề bài

Bài 1.

a. Tìm tập hợp các ước của 6; 10; 12; 13

b. Tìm tập hợp các bội của 4; 7; 8; 12

Đáp án

a. Ư (6) = {1; 2; 3; 6}

Ư (10) = {1; 2; 5; 10}

Ư (12) = {1; 2; 3; 4; 6; 12}

Ư (13) = {1; 13}

b. B (4) = {0; 4; 12; 16; 24…}

B(7) = {0; 7; 14; 21; 28; 35…}

B(8) = {0; 8; 16; 24; 32; 40…}

B (12) = {0; 12; 24; 36; 48…}

Bài 2. Tìm các số tự nhiên x sao cho:

a. x € Ư (12) và 2 <= x <= 8

b. x € B (5) và 20 <= x <= 36

c. x chia hết cho 5 và 13 < x <= 78

d. 12 chia hết cho x và x >4

Đáp án

a. Ta có Ư (12) = {1; 2; 3; 4; 6; 12}

Vì x € Ư (12) và 2 <= x <= 8 nên x € {2; 3; 4; 6}

b. x € B(5) và 20 < = x <= 36

Vì x € B(5) = {0; 5; 10; 15; 20; 25; 30; 35; 40…}

Mặt khác 20 <= x <= 36 => x € {20; 25; 30; 35}

c. ta có, x chia hết cho 5 và 13 < x <= 78

Vì x chia hết cho 5 nên x € B(5) => x € {0; 5; 10; 15; 20; 25; 30; 35; 40…}

Mặt khác 13 < x <= 78 => x € {15; 20; 25; 30; 35; 40; 45; 50; 55; 60; 65; 70; 75}

d. 12 chia hết cho x và x > 4

Vì 12 chia hết cho x nên x € Ư (12) = {1; 2; 3; 4; 6; 12} và x > 4 nên x € {6; 12}

Bài 3. Tìm tập hợp các số tự nhiên vừa là ước của 100 vừa là bội của 25

Đáp án

Gọi x là số tự nhiên cần tìm,

Ta có Ư (100) = {1; 2; 4; 5; 10; 20; 25; 50; 100}

Vì x thuộc B(25) nên x chia hết cho 25

=> x € {25; 50; 100}

Dạng 3. Toán có lời văn

Phương pháp giải:

Bước 1: Phân tích đề bài, chuyển bài toán về tìm ước, bội, ước chung, bội chung của các số cho trước
Bước 2: Áp dụng cách tìm ước, bội, ước chungm bội chung của các số cho trước

Bài 1. Có 20 viên bi. Bạn Minh muốn chia đều số viên bi vào các hộp, Tìm số hộp và số viên bi trong mỗi hộp. Biết không có hộp nào chứa 1 hay 20 viên bi.

Đáp án

Số hộp và số viên boi trong mỗi hộp phải là ước số của 20.

Ta cs: Ư (20) = {1; 2; 4; 5; 10; 20}

Vì không có hộp nào chứa 1 hau 20 viên bi nên số viên bi trong mỗi hộp chỉ có thể là 2; 4; 5; 10 tương ứng với số hộp là 10; 5; 4; 2.

Bài 2. Năm nay Bình 12 tuổi. Tuổi của mẹ Bình là bội số của tuổi Bình. Tìm tuổi của mẹ Bình biết tuổi của mẹ lớn hơn 30 và nhỏ hơn 45.

Đáp án

Gọi x là số tuổi của mẹ Bình (x € N, 30 < x < 45)

Tuổi của mẹ Bình là bội số của tuổi Bình nên x € B(12)

Mà 30 < x< 45 nên x = 36.

Vậy mẹ Bình 36 tuổi

Bài 3. Học sinh lớp 6A nhận được phần hưởng của nhà trường và mỗi em nhận được phần thưởng như nhau. Cô hiệu trưởng đã chia hết 129 quyển vở và 215 bút chì màu. Hỏi số học sinh lớp 6A là bao nhiêu

Đáp án

Ta thấy số phần thưởng là ƯC (129; 215)

Có ƯC (129; 125) = {1; 43}

Vì số học sinh lớp 6A không thể bằng 1 nên số học sinh lớp 6A là 43 học sinh.

Bài 4. Tính số học sinh của một trường biết rằng mỗi lần xeeos hàng 4, hàng 5, hàng 6, hàng 7 đều vừa đủ hàng và số học sinh của trường khoảng từ 415 đến 421 em.

Đáp án

Gọi số học sinh của trường là x ( x € N, 415 < x < 421)

Vì mỗi lần xép thành hàng 4, ahngf 5, hàng 6, hàng 7 đều vừa đủ hàng nên x chia hết cho 4; 5; 6; 7.

Tức là x € B (4; 5; 6; 7) = {0; 420; 840;…}

Mà 415 < x < 421 nên x = 420

Vậy số học sinh của trường là 420 học sinh.

Bài 5. Có 48 chiếc bút và 64 quyền vở. Cô giáo muốn chia số bút và số vở thành một số phần thưởng như nhau (Gồm cả bút và vở). Trong các cách chia sau, cách nào thực hiện được? Hãy điền vào chỗ trống …. những trường hợp chia được.

Cách chia	Số phần thưởng	Số bút ở mỗi phần thưởng	Số vở ở mỗi phần thường
Thứ nhất	8	…………..	……………..
Thứ hai	12	……………	……………….
Thứ ba	16	………………..	……………….

Đáp án

Số phần thưởng như nhau (gồm cả bút và vở) phải là ước chung của 48 và 64.

Trong ba số 8; 12; 16 thì chỉ có 8 và 16 là ước chung của 48 và 64

Vậy cách chia thứ nhất và thứ ba thực hiện được.

Cách chia thứ nhất:

Chia 48 chiếc bút thành 8 phần như nhua, thì số bút ở mỗi phần thưởng là 48 : 8 = 6 chiếc

Chia 64 quyền vở thành 8 phần thưởng như nhau, thì số vở ở mỗi phần thưởng là 64 : 8 = 8 quyền

Tương tự với cách chia thứ 3, ta có bảng sau:

Cách chia	Số phần thưởng	Số bút ở mỗi phần thưởng	Số vở ở mỗi phần thưởng
Thứ nhất	8	6	8
Thứ hai	12	…….	………..
Thứ ba	16	3	4

Bài tập vận dụng có đáp án

Câu 1: Trong các số sau, số nào là ước của 12?

A. 5

B. 8

C. 12

D. 24

Đáp án:

Ta có Ư(12) = {1; 2; 3; 4; 6; 12}

Chọn đáp án C.

Câu 2: Tìm tất cả các bội của 3 trong các số sau: 4; 18; 75; 124; 185; 258

A. {4; 75; 124}

B. {18; 124; 258}

C. {75; 124; 258}

D. {18; 75; 258}

Đáp án:

Ta có: 18 ⋮ 3, 75 ⋮ 3, 258 ⋮ 3 nên {18; 75; 258} là bội của 3

Chọn đáp án D.

Câu 3: Tìm x thuộc bội của 9 và x < 63

A. x ∈ {0; 9; 18; 28; 35}

B. x ∈ {0; 9; 18; 27; 36; 45; 54}

C. x ∈ {9; 18; 27; 36; 45; 55; 63}

D. x ∈ {9; 18; 27; 36; 45; 54; 63}

Đáp án:

Ta có:

⇒ x ∈ {0; 9; 18; 27; 36; 45; 54}

Chọn đáp án B.

Câu 4: Tìm x thuộc ước của 60 và x > 20

A. x ∈ {5; 15}

B. x ∈ {30; 60}

C. x ∈ {15; 20}

D. x ∈ {20; 30; 60}

Đáp án

Ta có:

Chọn đáp án B.

Câu 5: Tìm tập hợp các bội của 6 trong các số sau: 6; 15; 24; 30; 40

A. x ∈ {15; 24}

B. x ∈ {24; 30}

C. x ∈ {15; 24; 30}

D. x ∈ {6; 24; 30}

Đáp án

Trong các số trên thì B(6) = {6; 24; 30}

Chọn đáp án D.

b. Bài tập tự luận Ước và bội Toán lớp 6

Câu 6:

a) Tìm các bội của 4 trong các số sau: 8; 14; 20; 25.

b) Viết tập hợp các bội của 4 nhỏ hơn 30.

c) Viết dạng tổng quát các số là bội của 4.

Đáp án

a) Các bội của 4 trong các số sau: 8; 14; 20; 25 là 8 và 20.

b) Tập hợp các bội của 4 nhỏ hơn 30 là A = {0; 4; 8; 12; 16; 20; 24; 28}

c) Dạng tổng quát các số là bội của 4 là 4k với k ∈ N.

Câu 7: Tìm tất cả các số tự nhiên x sao cho

a) x ⋮ 15 và 45 < x < 136

b) 18 ⋮ x và x > 7

Đáp án

a) x ⋮ 15 nên x là bội số của 15

Mà 45 < x < 136

⇒ x ∈ (60; 75; 90; 105; 120; 135)

b) 18 ⋮ x nên x là ước của 18

Mà x > 7

⇒ x ∈ {9; 18}

Câu 8: Tìm hai số nguyên dương a, b biết [a, b] = 240 và (a, b) = 16.

Bài giải:

Do vai trò của a, b là như nhau, không mất tính tổng quát, giả sử a ≤ b.

Gọi d = (a, b) => a = md; b = nd với m, n thuộc Z+; (m, n) = 1

Do (a, b) = 16 nên a = 16m; b = 16n (m ≤ n do a ≤ b) với m, n thuộc Z+; (m, n) = 1.

Theo định nghĩa BCNN:

[a, b] = mnd = mn.16 = 240 => mn = 15

=> m = 1, n = 15 hoặc m = 3, n = 5 => a = 16, b = 240 hoặc a = 48, b = 80.

Chú ý: Ta có thể áp dụng công thức (**) để giải bài toán này: ab = (a, b).[a, b] => mn.162 = 240.16 suy ra mn = 15.

Câu 9: Có 15000 đồng có thể mua hai loại vở 2000 đồng và 5000 đồng (một cuốn). Hỏi có thể mua được bao nhiêu vở mỗi loại (mua cả 2 loại và mua hết số tiền đã mang theo).

Bài giải:

Ta có:

B(2000)={0,2000,4000,…}

B(5000)={0,5000,1000,…}

Vì 15000=5000+10000=5000.1+2000.5

Nên ta chọn mua 2 cuốn vở 5000 đồng và 5 cuốn vở 2000 đồng.

Câu 10: Một lớp có 30 nam và 18 nữ. Có bao nhiêu cách chia tổ sao cho số nam và số nữ chia đều cho mỗi tổ? Cách chia nào để mỗi tổ có số học sinh ít nhất?

Bài giải: Để tìm cách chia tổ mà số nam và số nữ chia đều ở mỗi tổ ta tìm ƯC(30;18)

Ta có: 30 = 22.3.5; 18 = 2.32

=> ƯCLN (30;18) = 2.3 = 6

Nên ƯC (30;18) = {1; 2; 3; 6}Ư

Có 3 cách chia tổ là 2 tổ; 3 tổ; 6 tổ (cách chia 1 tổ bỏ qua)

Cách chia tổ để học sinh mỗi tổ ít nhất là cách chia tổ chiều nhất (6 tổ)

=> Mỗi tổ có: 30 : 6 + 18 : 6 = 8 (học sinh)

Câu 11: Tìm các bội chung có ba chữ số của 5, 6 và 9

Bài giải:

B(5)={0,5,10,…}

B(6)={0,6,12,18,…}

B(9)={0,9,18,…}

Vậy BC(5,6,9)={0,90,180,270,…}

Các bội có ba chữ số: 180, 270, 360, 450, 540, 630, 720, 810, 900, 990,

Câu 12: Tìm hai số nguyên dương a, b biết ab = 180, [a, b] = 60.

Bài giải:

Từ ab = (a, b).[a, b] => (a, b) = ab/[a, b] = 180/60 = 3.

Tìm được (a, b) = 3, bài toán được đưa về dạng bài toán 2.

Kết quả: a = 3, b = 60 hoặc a = 12, b = 15.

Chú ý: Ta có thể tính (a, b) một cách trực tiếp từ định nghĩa ƯCLN, BCNN: Theo (*) ta có ab = mnd2 = 180; [a, b] = mnd = 60 => d = (a, b) = 3.

***

Trên đây là nội dung bài học Ước số là gì? Bội số là gì? Cách tìm ước và bội do thầy cô trường THCS Bình Chánh biên soạn và tổng hợp. Hy vọng sẽ giúp các em hiểu rõ nội dung bài học và từ đó hoàn thành tốt bài tập của mình. Đồng thời luôn đạt điểm cao trong các bài thi bài kiểm tra sắp tới. Chúc các em học tập thật tốt.

Đăng bởi THCS Bình Chánh trong chuyên mục Học tập