Giải Toán 6 Bài 35 Kết nối tri thức: Trung điểm của đoạn thẳng | Giải SGK Toán lớp 6

Trường THCS Bình Chánh 27/07/2023

Mời các em theo dõi nội dung bài học do thầy cô trường Trung học Bình Chánh biên soạn sẽ giúp các em nắm chắc kiến thức nội dung bài học tốt hơn.

Giải Toán 6 Bài 35: Trung điểm của đoạn thẳng

Giải Toán 6 trang 55 Tập 2

Bạn đang xem: Giải Toán 6 Bài 35 Kết nối tri thức: Trung điểm của đoạn thẳng | Giải SGK Toán lớp 6

Toán lớp 6 trang 55 Bài toán mở đầu: Em đã chơi bập bênh bao giờ chưa? Trong trò chơi này, người ta dùng một thanh gỗ dài gắn cố định trên một cái trục trên giá đỡ (H.8.35). Nếu hình dung thanh gỗ là một đoạn thẳng thì điểm đặt lên trục phải ở chính giữa đoạn thẳng đó.

Trong Hình học, điểm đó có ý nghĩa gì và làm thế nào để tìm nó?

Lời giải:

Sau bài học này ta sẽ biết điểm đó được gọi là trung điểm của đoạn thẳng.

Cách xác định: lấy đoạn thẳng đã cho chia đôi, ta tìm được điểm chính giữa đó.

Toán lớp 6 trang 55 Hoạt động 1: Người ta dùng một thanh gỗ dài 3 m để làm bập bênh. Theo em, điểm gắn trục phải cách hai đầu thanh gỗ là bao nhiêu?

Lời giải:

Điểm gắn trục phải nằm chính giữa thanh gỗ do đó điểm đó cách hai đầu thanh gỗ là : 3: 2 = 1,5 (m).

Vậy điểm gắn trục cách hai đầu thanh gỗ 1,5m.

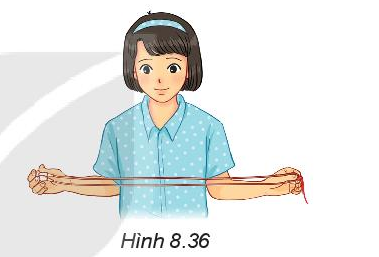
Toán lớp 6 trang 55 Hoạt động 2: Một sợi dây dài 120 cm. Gấp đôi sợi dây lại để hai đầu sợi dây trùng nhau. Đánh dấu điểm A là chỗ bị gập (H.8.36). Khoảng cách từ điểm A đến mỗi đầu sợi dây là bao nhiêu?

Lời giải:

Do sợi dây bị gập đôi và điểm A là chỗ bị gập nên khoảng cách điểm A đến mỗi đầu sợi dây là: 120 : 2 = 60 (m).

Vậy khoảng cách từ điểm A đến mỗi đầu sợi dây là 60m.

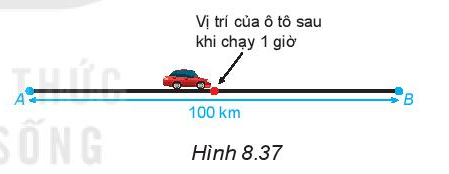
Toán lớp 6 trang 55 Hoạt động 3: Một chiếc xe chạy với vận tốc không đổi trên một quãng đường thẳng dài 100 km từ vị trí A đến vị trí B hết 2 giờ.

Hỏi sau khi chạy được 1 giờ, xe rời xa vị trí A bao nhiêu kilômét, còn cách vị trí B bao nhiêu kilômét (H.8.37)?

Lời giải:

Sau khi chạy được 1 giờ xe rời xa vị trí A:

100: 2 = 50 (km)

Sau khi chạy được 1 giờ, xe còn cách vị trí B là:

100 – 50 = 50 (km)

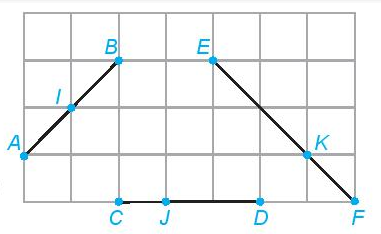
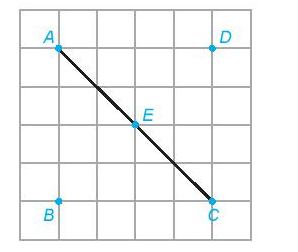
Toán lớp 6 trang 55 Câu hỏi: Dùng thước thẳng có vạch chia, em hãy kiểm tra xem các điểm I, J, K trong Hình 8.39 có lần lượt là trung điểm của các đoạn thẳng AB, CD, EF hay không.

Hình 8.39

Lời giải:

+) Ta thấy I nằm giữa hai điểm A và B và sử dụng thước thẳng đo ta có IA = IB nên I là trung điểm của AB

+) Ta thấy J nằm giữa hai điểm C và D và sử dụng thước thẳng đo ta thấy độ dài đoạn thẳng JC không bằng độ dài đoạn thẳng JD nên J không là trung điểm của CD

+) Ta thấy K nằm giữa hai điểm E và F và sử dụng thước thẳng đo ta có độ dài đoạn thẳng KE không bằng độ dài đoạn thẳng KF nên K không là trung điểm của EF.

Giải Toán 6 trang 56 Tập 2

Toán lớp 6 trang 56 Luyện tập: Cho đoạn thẳng PQ dài 12 đơn vị. Gọi E là trung điểm của đoạn thẳng PQ và F là trung điểm của đoạn thẳng PE. Tính độ dài đoạn thẳng EF.

Lời giải:

Vì E là trung điểm của đoạn thẳng PQ nên ta có:

PE = EQ = $\frac{12}{2}$ = 6 (đơn vị)

Vì F là trung điểm của đoạn thẳng PE nên ta có:

PF = EF = $\frac{6}{2}$ = 3 (đơn vị)

Vậy độ dài đoạn thẳng EF là 3 đơn vị.

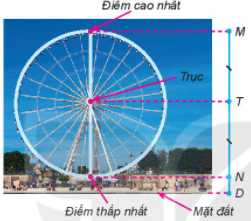
Toán lớp 6 trang 56 Vận dụng: Vòng quay mặt trời trong một khu vui chơi có điểm cao nhất là 60 m, điểm thấp nhất là 6 m (so với mặt đất). Hỏi trục của vòng quay nằm ở độ cao nào?

Lời giải:

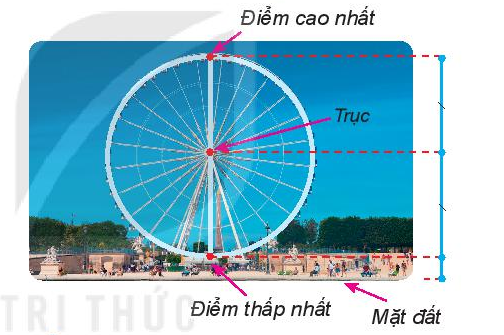
Gọi D là điểm ở mặt đất, T là trục, M là điểm cao nhất, N là điểm thấp nhất như hình vẽ dưới, do vậy ta có MD = 60m; ND = 6m

Vì điểm N nằm giữa hai điểm M và D nên:

MN + ND = MD

MN = MD – ND

Thay số: MD = 60m; ND = 6m ta được:

MN = 60 – 6 = 54m

Vì trục là tâm nên T là trung điểm MD do đó:

MT = TN = $\frac{MN}{2}$ = $\frac{54}{2}$ = 27 (m)

Vì N nằm giữa hai điểm T và D nên: TN + ND = TD

Thay số: TN = 27m; ND = 6m, ta có: TD = 27 + 6 = 33 (m)

Vậy trục của vòng quay nằm ở độ cao 33m so với mặt đất.

Toán lớp 6 trang 56 Bài 8.15: Cho hình vẽ sau:

a) Em hãy dùng thước thẳng để kiểm tra xem điểm E có phải là trung điểm của đoạn AC không.

b) Kiểm tra xem E còn là trung điểm của đoạn thẳng nào khác có các đầu mút là các điểm đã cho.

Lời giải:

a) Sử dụng thước thẳng để đo ta thấy EA = EC

Vì E nằm giữa A và C mà AE = EC nên E là trung điểm của AC.

Ta nhận thấy ba điểm B, E, D cùng nằm trên một đường thẳng nên chúng thẳng hàng.

Sử dụng thước thẳng để đo ta thấy: BE = DE

Vì E nằm giữa B và D mà BE = ED nên E là trung điểm của BD.

Toán lớp 6 trang 56 Bài 8.16: Tính độ dài của đoạn thẳng AB nếu trung điểm I của đoạn thẳng AB nằm cách mút A một khoảng bằng 4,5 cm.

Lời giải:

Vì trung điểm I của AB nằm cách mút A một khoảng 4,5 cm nên ta có:

AB = 4,5. 2 = 9 (cm)

Vậy độ dài đoạn thẳng AB dài 9cm.

Toán lớp 6 trang 56 Bài 8.17: Cho hình vẽ sau. Biết C là trung điểm của đoạn thẳng AB, D là trung điểm của đoạn thẳng AC. Biết rằng CD = 2 cm, hãy tính độ dài đoạn thẳng AB.