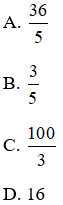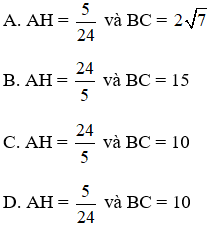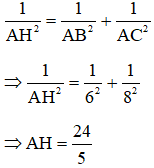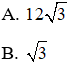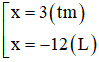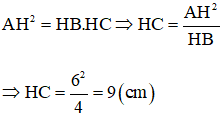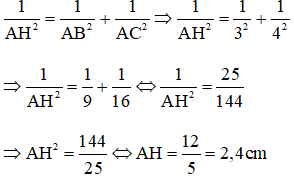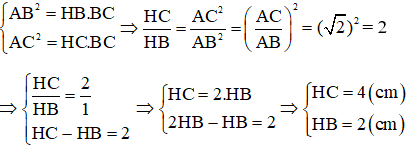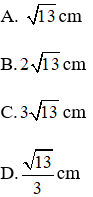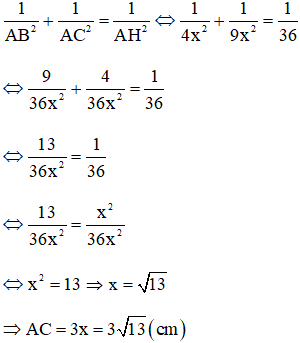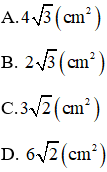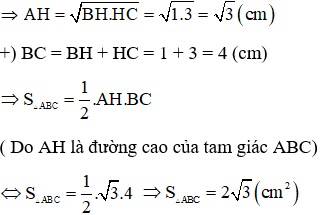Công thức tính cạnh huyền tam giác vuông và bài tập vận dụng

Cạnh huyền là gì trong tam giác vuông?

Cạnh huyền là cạnh dài nhất của một tam giác vuông và nó là cạnh nằm đối diện với góc vuông. Nó được liên hệ với các cạnh khác của tam giác vuông bằng định lý Pythagoras. Bình phương số đo cạnh huyền bằng tổng bình phương hai cạnh còn lại của tam giác vuông. Có thể dễ dàng nhận ra cạnh huyền trong tam giác vuông là cạnh lớn nhất.

Định nghĩa cạnh huyền trong hình học: Trong một tam giác vuông, cạnh dài nhất hoặc cạnh đối diện với góc vuông được gọi là cạnh huyền. Cạnh huyền liên hệ với đáy và đường cao của tam giác bằng công thức: Cạnh huyền bình phương = Cạnh đáy bình phương + Cạnh bên bình phương.

Bạn đang xem: Công thức tính cạnh huyền tam giác vuông và bài tập vận dụng

Các loại tam giác vuông

Chúng ta đã biết rằng một trong các góc trong tam giác vuông là 90º. Điều này có nghĩa rằng hai góc còn lại trong tam giác sẽ là góc nhọn. Có một số tam giác vuông đặc biệt là tam giác vuông cân và tam giác vuông vô hướng. Tam giác có cả hai góc còn lại bằng nhau được gọi là tam giác vuông cân và tam giác có hai góc còn lại có giá trị khác nhau được gọi là tam giác vuông cân.

Tam giác vuông cân: Một tam giác vuông cân được gọi là tam giác 90º-45º- 45º. Trong tam giác ABC, góc A = 90º; nên theo định nghĩa tam giác vuông, tam giác ABC là tam giác vuông. Ngoài ra AB = AC vì hai cạnh bằng nhau nên tam giác đó cũng là tam giác cân. Vì AB = AC nên các góc ở đáy bằng nhau. Chúng ta biết rằng tổng các góc của một tam giác là 180º. Do đó, các góc cơ sở cộng lại lên đến 90º, nghĩa là chúng bằng 45º mỗi góc. Vì vậy, trong một tam giác vuông cân, các góc sẽ luôn là 90º-45º- 45º.

Tam giác vuông vô hướng: Tam giác vuông vô hướng là tam giác có một góc bằng 90 ° và hai góc còn lại bằng 90º có các số đo khác nhau. Trong tam giác PQR, ∠Q = 90º, do đó, nó là một tam giác vuông. PQ không bằng QR, do đó, nó là một tam giác vô hướng. Ngoài ra còn có một trường hợp đặc biệt của tam giác vô hướng 30º-60º-90º cũng là tam giác vuông trong đó tỉ số giữa cạnh dài nhất của tam giác và cạnh ngắn nhất của nó là 2: 1. Cạnh đối diện với góc 30º là cạnh ngắn nhất.

Công thức tính cạnh huyền tam giác vuông

Để tìm ra một phương trình, một công thức của cạnh huyền đã từng có rất nhiều giả thuyết cùng tranh cãi giữa các nhà toán học từ nhiều thế kỷ trước. Phương trình giả thuyết: “Thực tế chỉ ra rằng với một tam giác vuông hoặc một tam giác có góc 90º, các hình vuông có thể được đóng khung bằng cách sử dụng mỗi ba cạnh của tam giác. Sau khi đặt các hình vuông đối diện với nhau, người ta quan sát thấy hình vuông lớn nhất có cùng diện tích với hai hình vuông còn lại. Để đơn giản hóa toàn bộ quan sát, sau này nó được đưa vào một phương trình ngắn cũng có thể được gọi là phương trình cạnh huyền.”

Trải qua nhiều giả thiết cùng tranh cãi chúng ta đã phương trình cạnh huyền như hiện tại:

Cạnh huyền = a bình phương + b bình phương = c bình phương.

Trong đó c là độ dài cạnh huyền và a và b là hai cạnh còn lại của tam giác vuông.

Những điểm sau đây sẽ giúp bạn hiểu rõ hơn về cạnh huyền và quan hệ của cạnh huyền với hai cạnh còn lại của tam giác vuông:

• Định lý Pythagoras phát biểu rằng trong một tam giác vuông, bình phương của cạnh huyền (cạnh dài nhất) bằng tổng bình phương của hai cạnh còn lại (cạnh đáy và vuông góc ).
• Phương trình cạnh huyền được biểu diễn dưới dạng: Cạnh huyền bình phương = cạnh đáy bình phương + cạnh bên bình phương.
• Phương trình hoành độ là a bình phương + b bình phương = c bình phương. Ở đây, a và b là chân của tam giác vuông và c là cạnh huyền.

Để tìm độ dài cạnh huyền của một tam giác, chúng ta sẽ sử dụng phương trình trên. Vì vậy, chúng ta nên biết các giá trị của đáy và cạnh bên góc vuông của tam giác. Ví dụ, trong một tam giác vuông, nếu độ dài của cạnh đáy là 3cm và độ dài của cạnh vuông góc là 4cm thì độ dài cạnh huyền có thể được tìm thấy bằng cách sử dụng công thức Cạnh huyền bình phương = cạnh đáy bình phương + cạnh bên bình phương. Bằng cách thay thế các giá trị của cơ sở và vuông góc, chúng ta nhận được cạnh huyền bình phương = 32 + 42 = 9 + 16 = 25. Tức dài của cạnh huyền là 5cm. Đây là cách chúng ta có thể tìm độ dài cạnh huyền bằng cách sử dụng phương trình cạnh huyền.

Làm theo các bước dưới đây để tìm độ dài cạnh huyền trong một tam giác vuông:

• Bước 1: Nhận biết giá trị của mặt đáy và cạnh vuông góc.
• Bước 2: Thay các giá trị của cơ sở và vuông góc vào công thức: Cạnh huyền bình phương = cạnh đáy bình phương + cạnh bên bình phương.
• Bước 3: Giải phương trình và nhận đáp số.

Bài 1: Tìm giá trị của cạnh dài nhất của miếng bánh mì có dạng tam giác vuông với chiều cao vuông góc cho trước là 12 inch và đáy là 5 inch.

Lời giải:

Các kích thước cho trước là vuông góc (P) = 12cm và cơ sở (B) = 5cm. Đưa các kích thước đã cho vào công thức H 2 = B 2 + P 2, ta nhận được:

H 2 = 5 2 + 12 2

H = √ {25 + 144} = √169cm

H = 13cm.

Do đó chiều dài cạnh huyền (cạnh dài nhất) của lát bánh mì là 13cm.

Bài 2: Trong một tam giác vuông, cạnh huyền là 5 đơn vị và cạnh vuông góc là 4 đơn vị. Tìm số đo cạnh đáy của tam giác.

Lời giải:

Các kích thước cho trước là vuông góc (P) = 4cm và cạnh huyền (H) = 5cm. Ta biết rằng (H) 2 = (B) 2 + (P) 2 ⇒ (B) 2 = (H) 2 – (P) 2.

Đưa các kích thước đã cho vào công thức, ta được:

B 2 = (5) 2 – (4) 2

B = √ {25-16}

B = √9 = 3cm

Do đó, chiều dài của cơ sở là 3cm.

Bài 3: Cho một tam giác vuông có hai cạnh góc vuông lần lượt là 6cm và 8cm. Tính cạnh huyền tam giác vuông đã cho.

Giải

Áp dụng công thức đã học, cạnh huyền của tam giác vuông đó là:

c^2 =6^2 + 8^2 = 100 => c = căn bậc hai của 100 = 10

Vậy cạnh huyền của tam giác vuông đã cho bằng 10(cm).

Bài 4: Cho ∆EDF vuông tại E, biết ED = 3cm, EF = 4cm. Tính chiều dài cạnh DF

Giải

Áp dụng định lý Pytago ta có:

a = ED = 3cm, b = EF = 4cm

c^2 = a^2+ b^2 = 3^2 + 4^2 = 9 + 16 = 25 => c = 5cm

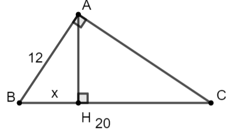
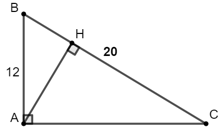
Bài 5: Giá trị của x trong hình bên là bao nhiêu biết BC = 20, AB = 12

Bài giải:

Áp dụng hệ thức lượng trong tam giác vuông ta có:

AB² = BH.BC

⇔ 12² = x.20

⇒ x = 

Đáp án A.

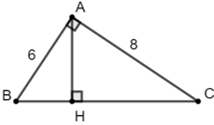
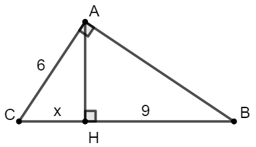
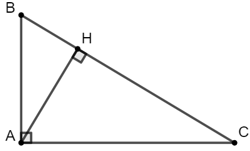
Bài 6: Tìm AH, BC với các giá trị như hình bên.

Bài giải:

+) Áp dụng định lý Pytago cho tam giác vuông ABC ta có:

BC² = AB² + AC²

⇒ BC² = 6² + 8² = 100 ⇒ BC = 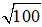 = 10

+) Áp dụng hệ thức lượng trong tam giác ABC vuông tại A có đường cao AH:

Đáp án C.

Bài 7: Cho tam giác ABC vuông tại A, đường cao AH. Biết AC = 6cm, BH = 9cm. Tính độ dài BC.

C. 3

D. 12

Bài giải:

Đặt HC = x (x > 0)⇒ BC = x + 9

Áp dụng hệ thức lượng trong tam giác vuông ta có:

AC² = BC.HC

⇔ 6² = (x + 9). x

⇔ x² + 9x – 36 = 0

⇔ x² + 12x – 3x – 36 = 0

⇔ x(x + 12) – 3(x + 12) = 0

⇔ (x – 3)(x + 12) = 0

⇒ 

Vậy BC = BH + CH = 9 + 3 = 12cm

Đáp án D.

Bài 8: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 12cm, BC = 20cm. Tính HC.

A. 6,4cm

B. 7,2cm

C. 12,8cm

D. 16,4cm

Bài giải:

Theo hệ thức lượng trong tam giác vuông ta có:

AB² = HB.BC ⇒ HB = 

⇒ HB = 7,2cm

⇒ HC = BC = HB = 20 – 7,2 = 12,8cm

Đáp án C.

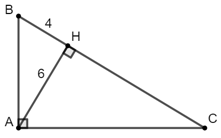
Bài 9: Cho tam giác ABC vuông tại A, đường cao AH. Biết AH = 6cm, HB = 4cm. Tính BC.

A. 10cm

B. 11cm

C. 12 cm

D. 13 cm

Bài giải:

Áp dụng hệ thức lượng trong tam giác vuông ta có:

⇒ BC = BH + HC = 4 + 9 = 13 (cm)

Đáp án D.

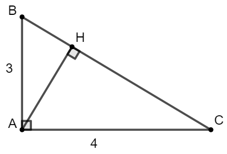
Bài 10: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 3cm, AC = 4cm. Tính AH.

A. 5,6 cm

B. 2,4 cm

C. 3,6 cm

D. 3,4 cm

Bài giải:

Theo hệ thức lượng trong tam giác vuông ABC ta có:

Đáp án B.

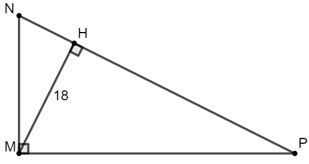
Bài 11: Cho ΔMNP vuông tại M, đường cao MH = 18cm. Biết HN : HP = 1 : 4. Tính độ dài cạnh huyền NP.

A. 36 cm

B. 45 cm

C. 54 cm

D. 63 cm

Bài giải:

Gọi HN = x (x > 0) thì HP = 4x

Theo hệ thức lượng trong tam giác vuông ta có:

MH² = HN.HP

⇔ 18² = x.4x

⇔ 4x² = 324

⇔ x² = 81

⇔ x = 9 (cm)

⇒ HN = 9 cm và HP = 4x = 4.9 = 36 cm

Vậy NP = HN + HP = 9 + 36 = 45 cm

Đáp án B.

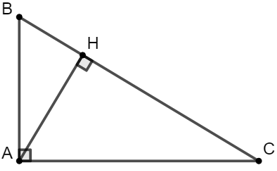
Bài 12: Cho tam giác ABC vuông tại A, đường cao AH. Cho biết AC : AB = 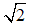 và HC – HB = 2cm. Độ dài HC bằng:

A. 4 cm

B. 2 cm

C. 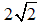 cm

D. 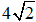 cm

Bài giải:

Áp dụng hệ thức lượng trong tam giác vuông ABC ta có:

Đáp án A.

Bài 13: Cho tam giác ABC vuông tại A có AB : AC = 2 : 3 và đường cao AH bằng 6cm. Khi đó độ dài đoạn thẳng AC bằng:

Bài giải:

Gọi AB = 2x (x > 0) thì AC = 3x

Áp dụng hệ thức lượng trong tam giác vuông ABC ta có:

Đáp án C.

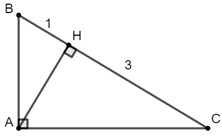
Bài 14: Cho tam giác ABC vuông ở A, đường cao AH. Biết HC = 3cm; HB = 1cm. Tính diện tích tam giác ABC.

Bài giải:

Xét tam giác ABC vuông ở A có đường cao AH:

+) AH² = HB.HC( Hệ thức lượng trong tam giác)

Đáp án B.

***

Trên đây là nội dung bài học Công thức tính cạnh huyền tam giác vuông và bài tập vận dụng do thầy cô trường THCS Bình Chánh biên soạn và tổng hợp. Hy vọng sẽ giúp các em hiểu rõ nội dung bài học và từ đó hoàn thành tốt bài tập của mình. Đồng thời luôn đạt điểm cao trong các bài thi bài kiểm tra sắp tới. Chúc các em học tập thật tốt.

Đăng bởi THCS Bình Chánh trong chuyên mục Học tập