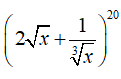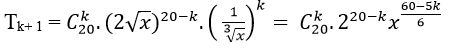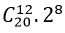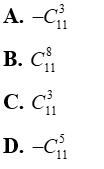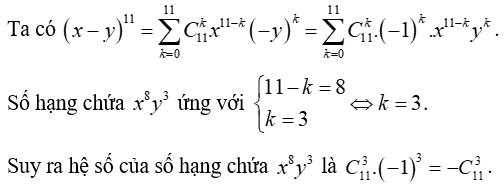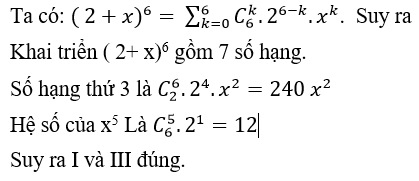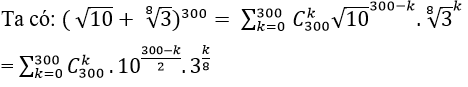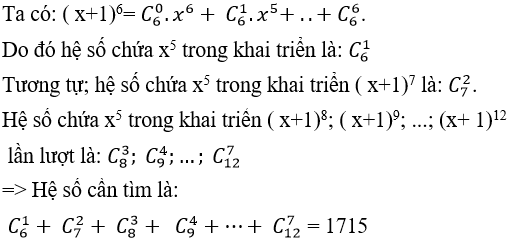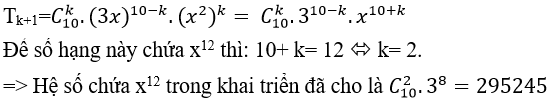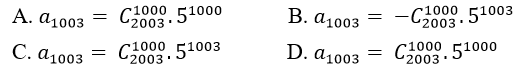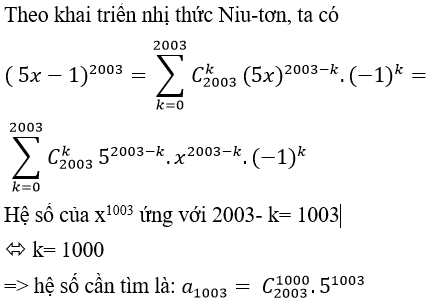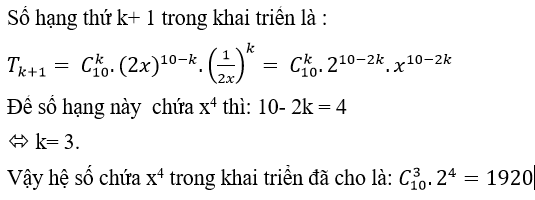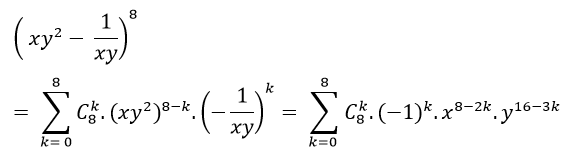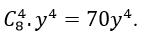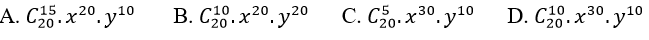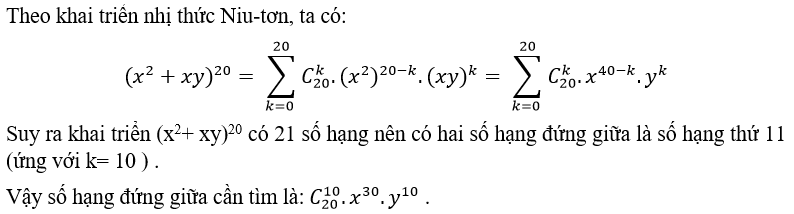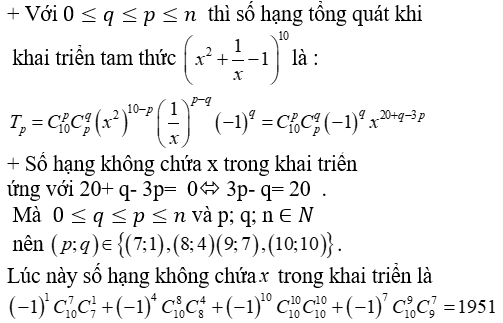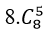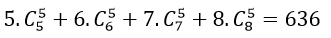Công thức nhị thức Newton và bài tập vận dụng

Cô Nguyễn Thanh Phương 23/05/2023

Mời các em theo dõi nội dung bài học về Công thức nhị thức Newton và bài tập vận dụng do thầy cô trường THCS Bình Chánh biên soạn. Hy vọng sẽ là tài liệu hữu ích giúp các em học tốt và hoàn thành tốt bài tập của mình.

Mục lục

Công thức nhị thức Newton

Tổ hợp là gì?

Định nghĩa: Giả sử tập A cơ n phần tử. Mỗi tập con gồm k phần tử của A được gọi là một tổ hợp chập k của n phần tử đã cho.

Kí hiệu: là số tổ hợp chập k của n phần tử . Ta có định lí, số các tổ hợp chập k của n phần tử đã cho.

Bạn đang xem: Công thức nhị thức Newton và bài tập vận dụng

$C_{n}^{k}=\frac{n!}{k!\left( n-k \right)!}=\frac{\left( n-1 \right)\left( n-2 \right)\left( n-3 \right)...\left( n-k+1 \right)}{k!}$

– Tính chất chập k của n phần tử:

Tính chất 1:
Tính chất 2: Công thức pascal

Công thức Nhị thức Newton

a. Định lí: Với _{^{với cặp số}} ta có:

${{\left( a+b \right)}^{n}}=\sum\limits_{k=0}^{n}{C_{n}^{k}{{a}^{n-k}}}{{b}^{k}}=C_{n}^{0}{{a}^{n}}+C_{n}^{1}{{a}^{n-1}}b+C_{n}^{2}{{a}^{n-2}}{{b}^{2}}+...+C_{n}^{n-1}{{a}^{1}}{{b}^{n-1}}+C_{n}^{n}{{b}^{n}}$

b. Hệ quả

Hệ quả: ${{\left( 1+x \right)}^{n}}=C_{n}^{0}+xC_{n}^{1}+{{x}^{2}}C_{n}^{2}+...+{{x}^{n}}C_{n}^{n}$

– Từ hệ quả trên ta rút được những kết quả sau đây:

${{2}^{n}}=C_{n}^{0}+C_{n}^{1}+C_{n}^{2}+...+C_{n}^{n}$

$C_{n}^{0}-C_{n}^{1}+C_{n}^{2}-C_{n}^{3}+...+{{\left( -1 \right)}^{n}}C_{n}^{n}=0$

c. Nhận xét

Trong khai triển Newton có tính chất sau:

– Gồm n + 1 phần tử.

– Số mũ của a giảm từ n đến 0 và số mũ của b tăng từ 0 đến n.

– Tổng số mũ của a và b trong mỗi số hạng bằng n .

– Các hệ số có tính đối xứng .

– Số hạng tổng quát:

Chú ý:

Số hạng thứ nhất
Số hạng thứ k:

Công thức nhị thức Newton và bài tập vận dụng

Các công thức liên quan đến khai triển nhị thức Newton

${{\left( x+1 \right)}^{n}}=C_{n}^{0}{{x}^{n}}+C_{n}^{1}{{x}^{n-1}}+C_{n}^{2}{{x}^{n-2}}+...+C_{n}^{k}{{x}^{n-k}}+...C_{n}^{n-1}x+C_{n}^{n}$
${{\left( 1+x \right)}^{n}}=C_{n}^{0}+C_{n}^{1}x+C_{n}^{2}{{x}^{2}}+...+C_{n}^{k}{{x}^{k}}+...C_{n}^{n-1}{{x}^{n-1}}+C_{n}^{n}{{x}^{n}}$
${{\left( x-1 \right)}^{n}}=C_{n}^{0}-C_{n}^{1}x+C_{n}^{2}{{x}^{2}}-...+{{\left( -1 \right)}^{k}}C_{n}^{k}{{x}^{k}}+...+{{\left( -1 \right)}^{n-1}}C_{n}^{n-1}{{x}^{n-1}}+{{\left( -1 \right)}^{n}}C_{n}^{n}{{x}^{n}}$
$C_{n}^{k}=C_{n}^{n-k}$
$C_{n}^{k}+C_{n}^{k+1}=C_{n+1}^{k+1},\left( n\ge 1 \right)$
$k.C_{n}^{k}=\frac{k.n!}{k!\left( n-k \right)!}==\frac{n.\left( n-1 \right)!}{\left( n-k \right)!.\left( k-1 \right)!}=n.C_{n-1}^{k-1}$
$\frac{1}{k+1}.C_{n}^{k}=\frac{k.n!}{\left( k+1 \right).k!\left( n-k \right)!}=\frac{n.\left( n-1 \right)!}{\left( n+1 \right)\left( n-k \right)!\left( k+1 \right)!}=\frac{1}{n+1}.C_{n+1}^{k+1}$

Một số công thức thường dùng trong các bài tập

$C_{n}^{k}=C_{n}^{n-k}$
$C_{n-1}^{k-1}+C_{n-1}^{k}=C_{n}^{k}$
$k.C_{n}^{k}=n.C_{n-1}^{k-1}$
$\frac{1}{k+1}.C_{n}^{k}=\frac{1}{n+1}.C_{n+1}^{k+1}$
${{2}^{n}}=C_{n}^{0}+C_{n}^{1}+C_{n}^{2}+...+C_{n}^{n}$
${{2}^{n-1}}=C_{n}^{0}+C_{n}^{2}+{{C}_{n}}^{4}+...+C_{n}^{2\left[ \frac{n}{2} \right]}$
${{2}^{n-1}}=C_{n}^{1}+C_{n}^{3}+C_{n}^{{}}+...+C_{n}^{2\left[ \frac{n-1}{2} \right]+1}$

Công thức Newton mở rộng

$C_{n}^{k}+2C_{n}^{k+1}+C_{n}^{k+2}=C_{n+2}^{k+2}$
$C_{n}^{k}+3C_{n}^{k+1}+3C_{n}^{k+2}+C_{n}^{k+3}=C_{n+3}^{k+3}$

Dấu hiệu sử dụng nhị thức Newton

a. Chứng minh đẳng thức hay bất đẳng thức mà có: $\sum\limits_{i=1}^{n}{C_{n}^{1}}$

b. Biểu thức có $\sum\limits_{i=1}^{n}{i\left( i-1 \right)C_{n}^{i}}$ thì dùng đạo hàm

c. Biểu thức có $\sum\limits_{i=1}^{n}{\left( i+k \right)C_{n}^{i}}$ thì ta nhân hai vế với ${{x}^{k}}$ rồi lấy đạo hàm

d. Biểu thức có $\sum\limits_{i=1}^{n}{{{a}^{k}}.C_{n}^{i}}$ thì ta chọn giá trị $x=a$ thích hợp

e. Biểu thức có $\sum\limits_{i=1}^{n}{\frac{1}{i-1}.C_{n}^{i}}$ ta lấy tích phân xác định trên $\left[ a,b \right]$ thích hợp

Tam giác Pascal

n=0 1

n=1 1 1

n=2 1 2 1

n=3 1 3 3 1

n=4 1 4 6 4 1

Tam giác Pascal được thiết lập theo quy luật

– Đỉnh được ghi số 1. Tiếp theo là hàng thứ nhất ghi hai số 1

– Nếu biết hàng thứ n thì hàng thứ n + 1 tiếp theo được thiết lập bằng cách cộng hai số liên tiếp của hàng thứ n rồi viết kết quả xuống hàng dưới ở vị trí giữa hai số này. Sau đó viết số 1 ở đầu và cuối hàng.

Bài tập vận dụng về nhị thức Newton

Ví dụ 1: Viết khai triển theo công thức nhị thức Newton:

$a. {{\left( a+2b \right)}^{5}}$

$b. {{\left( a-\sqrt{2} \right)}^{6}}$

$c. {{\left( x-\frac{1}{x} \right)}^{10}}$

Hướng dẫn giải

a. Khai triển Newton của

${{\left( a+2b \right)}^{5}}=C_{5}^{0}{{a}^{5}}+C_{5}^{1}{{a}^{4}}2b+...+C_{5}^{5}32{{b}^{5}}$

b. Khai triển Newton của

${{\left( a-\sqrt{2} \right)}^{6}}=C_{6}^{0}{{a}^{6}}+C_{6}^{1}{{a}^{5}}.\sqrt{2}+C_{6}^{2}{{a}^{4}}.2+...+C_{6}^{6}.{{\left( \sqrt{2} \right)}^{6}}$

c. Khai triển Newton của ${{\left( x-\frac{1}{x} \right)}^{10}}=\sum\limits_{k=0}^{10}{C_{10}^{k}.{{x}^{10-k}}.{{\left( \frac{-1}{x} \right)}^{k}}=}\sum\limits_{k=0}^{10}{C_{10}^{k}.{{x}^{10-k}}.\frac{{{\left( -1 \right)}^{k}}}{{{x}^{k}}}=\sum\limits_{k=0}^{10}{C_{10}^{k}.{{\left( -1 \right)}^{k}}{{x}^{10-2k}}}}$

Ví dụ 2: Tìm hệ số của trong khai triển biểu thức

Hướng dẫn giải

Ta có:

Số hạng chứa trong khai triển ứng với k = 7. Khi đó hệ số của số hạng chứa $C_{10}^{7}.{{\left( -2 \right)}^{7}}=-15360$

Ví dụ 3: Tìm hệ số không chứa x trong khai triển sau: biết rằng: $C_{n}^{n-1}+C_{n}^{n-2}=78,x>0$

Hướng dẫn giải

Ta có:

$\Leftrightarrow \frac{n!}{\left( n-1 \right)!(n-n+1)!}+\frac{n!}{\left( n-2 \right)!\left( n-2+2 \right)!}=78$

$\Leftrightarrow \frac{n!}{\left( n-1 \right)!(1)!}+\frac{n!}{\left( n-2 \right)!\left( 2 \right)!}=78$

$\Leftrightarrow n+\frac{n\left( n-1 \right)}{2}=78\Leftrightarrow {{n}^{2}}+n-156=0\Leftrightarrow \left[ \begin{matrix} n=12\left( TM \right) \\ n=-13\left( L \right) \\ \end{matrix} \right.$

Do đó biểu thức khai triển là

Số hạng không chứa x ứng với k:

Số hạng không chưa x là:

Ví dụ 4: Xét khai triển:

a. Viết số hạng thứ k + 1 trong khai triển.

b. Số hạng nào trong khai triển không chứa x.

c. Xác định hệ số của \[{{x}^{4}}\]trong khai triển.

Hướng dẫn giải

${{\left( 2x+\frac{1}{x} \right)}^{20}}=\sum\limits_{k=0}^{20}{C_{20}^{k}{{\left( 2x \right)}^{20-k}}{{\left( \frac{1}{x} \right)}^{k}}=}\sum\limits_{k=0}^{20}{C_{20}^{k}{{2}^{20-k}}{{x}^{20-2k}}}$

Số hạng không chứa x trong khai triển ứng với k là:

Số hạng không chứa x trong khai triển là:

Số hạng chứa trong khai triển ứng với k là:

Vậy số hạng chứa trong khai triển có hệ số là: $C_{20}^{8}{{.2}^{12}}$

Ví dụ 5: Tính tổng:

Hướng dẫn giải

Ta có:

Vì

$\Leftrightarrow S=\frac{1}{2\left( n+1 \right)}\sum\limits_{k=0}^{n}{{{\left( -1 \right)}^{k}}C_{n+1}^{k+1}}=\frac{-1}{2\left( n+1 \right)}\left( \sum\limits_{k=0}^{n+1}{{{\left( -1 \right)}^{k}}C_{n+1}^{k}-C_{n+1}^{0}} \right)=\frac{1}{2\left( n+1 \right)}$

Bài tập trắc nghiệm

Câu 1: Số hạng không chứa x trong khai triển là

Lời giải:

Đáp án : B

Ta có số hạng thứ k+ 1 là :

Số hạng không chứa x tương ứng với: (60-5k)/6=0

⇔ 60 – 5k= 0 ⇔ k= 12.

Do vậy số hạng cần tìm là:

Câu 2: Trong khai triển ( x – y)¹¹, hệ số của số hạng chứa x⁸y³ là:

Lời giải:

Đáp án : A

Câu 3: Trong khai triển nhị thức (2+ x)6 xét các khẳng định sau:

I. Gồm có 7 số hạng.

II. Số hạng thứ 3 là 16x.

III. Hệ số của x5 là 12.

Trong các khẳng định trên

A. Chỉ I và III đúng

B. Chỉ II và III đúng

C. Chỉ I và II đúng

D. Cả ba đúng

Lời giải:

Đáp án : A

Câu 4: Có bao nhiêu số hạng hữu tỉ trong khai triển .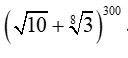

A.37

B.38

C.36

D.39

Lời giải:

Đáp án : B

⇒ k= 8t ( với t nguyên)

Lại có: 0≤k≤300 nên 0≤8t≤300

⇔ 0≤t≤37,5. Mà t nguyên nên t ∈ {0,1,2,3…, 37}.

Có 38 giá trị nguyên của t thỏa mãn. Suy ra có 38 giá trị của k thỏa mãn.

⇒ Có 38 số hạng hữu tỉ trong khai triển đã cho.

Câu 5: Tìm hệ số của x⁵ trong khai triển P(x) = ( x+1)⁶ +(x+ 1)⁷ + ( x+ 1)⁸ + ..+ (x+ 1)¹² .

A.1711

B.1287

C.1716

D.1715

Lời giải:

Đáp án : D

Câu 6: Tìm hệ số chứa x¹² trong khai triển ( 3x+ x²)¹⁰

A.145654

B.298645

C.295245

D.Đáp án khác

Lời giải:

Theo khai triển nhị thức Niu-tơn, ta có số hạng thứ k+ 1 trong khai triển là:

Câu 7: Khai triển đa thức P(x) = (5x – 1)²⁰⁰³ ta được :

P(x)= a₂₀₀₃.x²⁰⁰³ + a₂₀₀₂.x²⁰⁰² + …+ a₁x+ a₀.

Mệnh đề nào sau đây đúng?

Lời giải:

Đáp án : C

Câu 8: Tìm hệ số chứa x⁴ trong khai triển (2x+ 1/2x)¹⁰

A.1960

B.1920

C.1864

D.1680

Lời giải:

Đáp án : B

Câu 9: Tìm số hạng không chứa x trong khai triển: ( xy²– 1/xy)⁸

A.70y⁴

B.25y⁴

C.50y⁵

D.80y⁴

Lời giải:

Theo khai triển nhị thức Niu-tơn, ta có:

Số hạng không chứa x ứng với: 8 – 2k=0 ⇔ k= 4

⇒ số hạng cần tìm

Câu 10: Tìm số hạng đứng vị trí chính giữa trong khai triển: ( x²+ xy)²⁰

Lời giải:

Đáp án : D

Theo khai triển nhị thức Niu-tơn, ta có:

Câu 11: Khai triển đa thức: P(x)= ( 2 x- 1)¹⁰⁰⁰ ta được:

P(x)= a₁₀₀₀x¹⁰⁰⁰ + a₉₉₉x⁹⁹⁹+ ….+ a₁x+ a₀ .Tính a₁₀₀₀ + a₉₉₉ + …+ a₁ + a₀ ?

A.-1

B.0

C.2

D.1

Lời giải:

Đáp án : D

Ta có: (x) = a₁₀₀₀x¹⁰⁰⁰ + a₉₉₉x⁹⁹⁹+ ….+ a₁x+ a₀

Cho x = 1 ta được P(1) = a₁₀₀₀ + a₉₉₉ + a₉₉₈ + …+ a₁+ a₀ (1)

Mặt khác: P(x) = ( 2x-1)¹⁰⁰⁰ nên P(1)= (2.1 – 1)¹⁰⁰⁰ = 1 (2)

Từ (1) và (2) suy ra: a₁₀₀₀ + a₉₉₉ + a₉₉₈ + …+ a₁+ a₀ = 1

Câu 12: Tìm hệ số của x⁵ trong khai triển P(x) = x.(2+ x)⁵ + x²( 1 + x )¹⁰

A.110

B.120

C.130

D.140

Lời giải:

Đáp án : C

Câu 13: Số hạng không chứa x trong khai triển (x² + 1/x – 1)¹⁰ là

A.1951

B.1950

C.3150

D.-360

Lời giải:

Đáp án : A

Câu 14: Số hạng chứa x⁸ trong khai triển (x³ – x² -1)⁸ là

A.168x⁸

B.168

C.238x⁸

D.238

Lời giải:

Đáp án : D

Câu 15: Tìm hệ số của x⁵ trong khai triển P(x)= (1+ x)+ 2(1+x)² + …+ 8(1+x)⁸

A.487

B.636

C.742

D.568

Lời giải:

Đáp án : B

Các biểu thức ( 1 + x ) ; 2( 1 + x )² ; 3(1+x)³ ; 4(1+ x)⁴ không chứa số hạng chứa x⁵

Hệ số của số hạng chứa x5 trong khai triển 5(1+x)⁵ là

Hệ số của số hạng chứa x5 trong khai triển 6(1+x)⁶ là

Hệ số của số hạng chứa x5 trong khai triển 7(1+x)⁷ là

Hệ số của số hạng chứa x5 trong khai triển 8(1+ x)⁸ là

Vậy hệ số của x₅ trong khai triển P(x) là :

***

Trên đây là nội dung bài học Công thức nhị thức Newton và bài tập vận dụng do thầy cô trường THCS Bình Chánh biên soạn và tổng hợp. Hy vọng sẽ giúp các em hiểu rõ nội dung bài học và từ đó hoàn thành tốt bài tập của mình. Đồng thời luôn đạt điểm cao trong các bài thi bài kiểm tra sắp tới. Chúc các em học tập thật tốt.

Đăng bởi THCS Bình Chánh trong chuyên mục Học tập