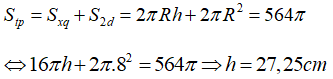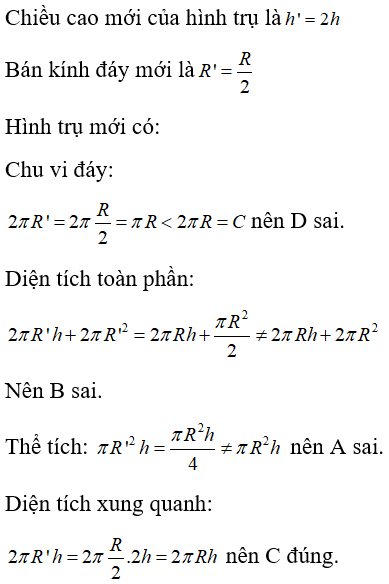Mời các em theo dõi nội dung bài học về Diện tích xung quanh hình trụ và bài tập vận dụng do thầy cô trường THCS Bình Chánh biên soạn. Hy vọng sẽ là tài liệu hữu ích giúp các em học tốt và hoàn thành tốt bài tập của mình.
Hình trụ là gì?
Hình trụ là hình được giới hạn bởi hai đường tròn có đường kính bằng nhau và mặt trụ.
Hình trụ tròn là hình trụ khi quay hình chữ nhật quanh trục cố định, ta sẽ có hình trụ.
Diện tích xung quanh hình trụ
Diện tích hình trụ là toàn bộ không gian chiếm giữ bằng cách tính tổng diện tích xung quanh và diện tích hai đáy. Trong khi đó, diện tích toàn phần hình trụ là diện tích của mặt xung quanh hình trụ, không gồm diện tích hai đáy.
Bạn đang xem: Diện tích xung quanh hình trụ và bài tập vận dụng
Công thức tính diện tích xung quanh
+ r: bán kính hình trụ
+ h: chiều cao nối từ đáy tới đỉnh hình trụ (hay còn gọi là đường sinh)
Công thức tính diện tích toàn phần
Trong đó:
+ r: bán kính hình trụ
+ 2 x π x r x h : diện tích xung quanh hình trụ
+ 2 x π x r2: diện tích của hai đáy
Ví dụ
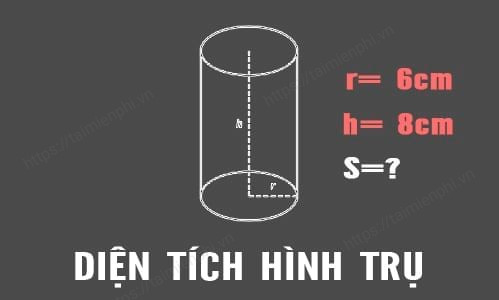
Ví dụ 1: Cho một hình trụ có bán kính đường tròn đáy là 6 cm, trong khi đó chiều cao nối từ đáy tới đỉnh hình trụ dày 8 cm. Hỏi diện tích xung quanh và diện tích toàn phần của hình trụ bằng bao nhiêu?
Theo công thức ta có bán đường tròn đáy r = 6 cm và chiều cao của hình trụ h = 8 cm . Suy ra ta có công thức tính diện tích xung quanh hình trụ và diện tích toàn phần hình trụ bằng:
– Diện tích xung quanh hình trụ = 2 x π x r x h = 2 x π x 6 x 8 = ~ 301 cm2
– Diện tích toàn phần hình trụ = 2 Π x R x (R + H) = 2 X π x 6 x (6 + 8) = ~ 527 cm2
Ví dụ 2: Tính diện tích xung quanh hình trụ bán kính 2 chiều cao 4
Áp dụng công thức, tương tự tính được diện tích xung quanh của hình trụ là: 50.24
Ví dụ 3: Tính diện tích xung quanh hình trụ có chiều cao 20m chu vi đáy bằng 5m
Lưu ý: Ngoài các dạng bài tập tính diện tích xung quanh hình trụ ở trên, toán lớp 9 còn phổ biến với các bài tập yêu cầu tính diiện tích xung quanh hình trụ có đường sinh I và bán kính đáy r. Đường sinh ở đây được hiểu là chiều cao của hình lăng trụ. Các em có thể thay số vào công thức và tính như bình thường.
Công thức và vách tính thể tích hình trụ
Thể tích hình trụ là lượng không gian được chiếm giữ một hình trụ nhất định. Thể tích hình trụ sử dụng đơn vị đo là lập phương của khoảng cách (mũ 3 khoảng cách).
Trong đó:
– r: bán kính hình trụ
– h: chiều cao hình trụ
Ví dụ:
Cho một lăng trụ bất kỳ có bán kính mặt đáy r = 4 cm , trong khi đó, chiều cao nối từ đỉnh của hình trụ xuống đáy hình trụ có độ dài h = 8 cm . Hỏi thể tích của hình trụ này bằng bao nhiêu?
Theo đó, ta áp dụng vào công thức tính thể tích hình trụ và có: bán kính mặt đáy hình trụ r = 4cm và chiều cao hình trụ h = 8cm. Suy ra, ta có công thức tính thể tích hình trụ như sau:
V = π x r2 x h = π x 42 x 8 = ~ 402 cm3
Bài tập vận dụng
Câu 1: Cho hình trụ có chu vi đáy là 8π và chiều cao h = 10. Tính thể tích hình trụ:
A. 80π
B. 40π
C. 160π
D. 150π
Chọn đáp án C.
Câu 2: Cho hình trụ có bán kính đáy R = 4 (cm) và chiều cao h = 5 (cm). Diện tích xung quanh của hình trụ là:
A. 40π
B. 30π
C. 20π
D. 50π
Diện tích xung quanh của hình trụ là:
Sxq = 2πRh = 2π.4.5 = 40π (cm2)
Chọn đáp án A.
Câu 3: Cho hình trụ có bán kính đáy R = 8cm và diện tích toàn phần 564π cm2. Tính chiều cao của hình trụ:
A. 27cm
B. 27,25cm
C. 25cm
D. 25,27cm
Ta có diện tích toàn phần của hình trụ:
Chọn đáp án B.
Câu 4: Cho hình trụ có bán kính đáy R và chiều cao h. Nếu ta tăng chiều cao lên hai lần và giảm bán kính đáy đi hai lần thì:
A. Thể tích hình trụ không đổi
B. Diện tích toàn phần không đổi
C. Diện tích xung quanh không đổi
D. Chu vi đáy không đổi
Chọn đáp án C.
Câu 5: Hộp sữa Ông Thọ có dạng hình trụ (đã bỏ nắp) có chiều cao h = 12cm và đường kính đáy h = 8cm. Tính diện tích toàn phần của hộp sữa. Lấy π ≃ 3,14
A. 110π (cm2)
B. 128π (cm2)
C. 96π (cm2)
D. 112π (cm2)
Diện tích toàn phần của hộp sữa:
Chọn đáp án D.
Câu 6: Chiều cao của 1 hình trụ bằng bán kính đường tròn đáy. Diện tích xung quanh của hình trụ là 628cm2. Tính thể tích hình trụ.
A. 1000π
B. 100π
C. 500π
D.Đáp án khác
Chọn đáp án A.
Câu 7: Một hình trụ có bán kính đáy R = 2cm và diện tích xunh quanh là Sxq = 100π . Tính diện tích toàn phần của hình trụ?
A. 140π
B. 104π
C. 120π
D. 108π
Chọn đáp án B.
Câu 8: Tính diện tích xung quanh của một hình trụ có chu vi đường tròn đáy là 4π và chiều cao h =2.
A. 12π
B. 4π
C. 8π
D. 16π
Chọn đáp án C.
Câu 9: Cho một hình trụ có diện tích xung quanh bằng diện tích hai đáy. Khi đó:
A. r = 2h
B. h = 2r
C. h = 4r
D. r = h
Vì diện tích xung quanh bằng diện tích hai đáy nên:
Chọn đáp án D.
Câu 10: Nếu tăng bán kính đáy của hình trụ lên 4 lần và giữ nguyên chiều cao thì thể tích mới của hình trụ”
A. Gấp 4 lần
B. Gấp 8 lần
C. Gấp 12 lần
D. Gấp 16 lần
Chọn đáp án D.
Câu 11: Cho hình trụ có bán kính đáy R = 12 cm và diện tích toàn phần 672π cm2. Tính chiều cao của hình trụ
A. 16cm
B. 18cm
C. 8cm
D. 20cm
Lời giải:
Đáp án cần chọn là: A
Câu 12: Cho hình trụ có bán kính đáy R và chiều cao h. Nếu ta tăng chiều cao lên hai lần và giảm bán kính đáy đi hai lần thì
A. Thể tích hình trụ không đổi
B. Diện tích toàn phần không đổi
C. Diện tích xung quanh không đổi
D. Chu vi đáy không đổi
Lời giải:
Chiều cao mới của hình trụ là h’ = 2h; bán kính mới là
Hình trụ mới có:
Chu vi đáy = C nên Phương án D sai
Diện tích toàn phần nên Phương án B sai
Thể tích nên Phương án A sai
Diện tích xung quanh nên Phương án C đúng
Đáp án cần chọn là: C
Câu 13: Chọn câu đúng. Cho hình trụ có bán kính đáy R và chiều cao h. Nếu ta giảm chiều cao đi chín lần và tăng bán kính đáy lên ba lần thì
A. Thể tích hình trụ không đổi
B. Diện tích toàn phần không đổi
C. Diện tích xung quanh không đổi
D. Chu vi đáy không đổi
Lời giải:
Chiều cao mới của hình trụ là ; bán kính đáy mới là R’ = 3R
Hình trụ mới có:
Chu vi đáy 2πR’ = 2π.3R = 6πR = 3.2πR = 3C nên phương án D sai
Thể tích nên phương án A đúng
Diện tích xung quanh nên phương án C sai
Đáp án cần chọn là: A
Câu 14: Hộp sữa ông Thọ có dạng hình trụ (đã bỏ nắp) có chiều cao h = 12cm và đường kính đáy là d = 8cm. Tính diện tích toàn phần của hộp sữa. Lấy π ≈ 3,14
A. 110π (cm2)
B. 128π (cm2)
C. 96π (cm2)
D. 112π (cm2)
Lời giải:
Bán kính đường tròn đáy R = = 4cm nên diện tích một đát Sd = πR2 = 16π (cm2)
Ta có diện tích xung quanh của hình trụ Sxq = 2πRh = 2π.4.12 = 96 (cm2)
Vì hộp sữa đã mất nắp nên diện tích toàn phần của hộp sữa
Stp = 96π + 16π = 112π (cm2)
Đáp án cần chọn là: D
*Chú ý: Một số bạn sẽ tính diện tích toàn phần bằng tổng diện tích xung quanh với diện tích hai đáy nhưng hộp sữa ở đây đã mất nắp nên chỉ còn một đáy. Khi tính ta chỉ cần lấy tổng diện tích xung quanh với diện tích một đáy
Câu 15: Hộp sữa ông Thọ có dạng hình trụ (đã bỏ nắp) có chiều cao h = 10cm và đường kính đáy là d = 6cm. Tính diện tích toàn phần của hộp sữa. Lấy π ≈ 3,14
A. 110π (cm2)
B. 129π (cm2)
C. 96π (cm2)
D. 69π (cm2)
Lời giải:
Bán kính đường tròn đáy R = = 3cm nên diện tích một đát Sd = πR2 = 9 (cm2)
Ta có diện tích xung quanh của hình trụ Sxq = 2πRh = 2π.3.10 = 60 (cm2)
Vì hộp sữa đã mất nắp nên diện tích toàn phần của hộp sữa
Stp = 9π + 60π = 69π (cm2)
Đáp án cần chọn là: D
*Chú ý: Một số bạn sẽ tính diện tích toàn phần bằng tổng diện tích xung quanh với diện tích hai đáy nhưng hộp sữa ở đây đã mất nắp nên chỉ còn một đáy. Khi tính ta chỉ cần lấy tổng diện tích xung quanh với diện tích một đáy
***
Trên đây là nội dung bài học Diện tích xung quanh hình trụ và bài tập vận dụng do thầy cô trường THCS Bình Chánh biên soạn và tổng hợp. Hy vọng sẽ giúp các em hiểu rõ nội dung bài học và từ đó hoàn thành tốt bài tập của mình. Đồng thời luôn đạt điểm cao trong các bài thi bài kiểm tra sắp tới. Chúc các em học tập thật tốt.
Đăng bởi THCS Bình Chánh trong chuyên mục Học tập
- Hãy viết một bài văn trình bày suy nghĩ của em về vấn đề ô nhiễm môi trường hiện nay (25 mẫu)
- Rừng là lá phổi xanh của nhân loại. Em hãy viết bài văn trình bày suy nghĩ của em về ý kiến trên (5 mẫu)
- Bạo lực học đường đang là vấn đề được cả xã hội quan tâm. Em hãy viết một bài văn trình bày suy nghĩ của em về vấn đề trên (51 mẫu)
- Viết một đoạn văn ngắn nói về cảm xúc của em khi được thưởng thức một tác phẩm văn nghệ (truyện, thơ, phim, ảnh, tượng,…), trong đoạn văn đó có câu chứa thành phần tình thái hoặc cảm thán (25 mẫu)
- Nêu một tác phẩm văn nghệ mà em yêu thích và phân tích ý nghĩa, tác động của tác phẩm ấy đối với mình (9 mẫu)
- Phân tích Tiếng nói của văn nghệ của Nguyễn Đình Thi lớp 9 hay nhất (17 mẫu)