Giải Toán 7 Kết nối tri thức: Luyện tập chung trang 71
Mời các em theo dõi nội dung bài học do thầy cô trường Trung học Bình Chánh biên soạn sẽ giúp các em nắm chắc kiến thức nội dung bài học tốt hơn.
Giải bài tập Toán 7 : Luyện tập chung trang 71
Bài 9.14 trang 71 Toán 7 Tập 2:
Bạn đang xem: Giải Toán 7 Kết nối tri thức: Luyện tập chung trang 71
Hãy giải thích: Nếu M là một điểm tùy ý nằm trên cạnh BC hoặc CD của hình vuông ABCD thì độ dài đoạn thẳng AM luôn lớn hơn hoặc bằng độ dài cạnh của hình vuông đó (H.9.21).
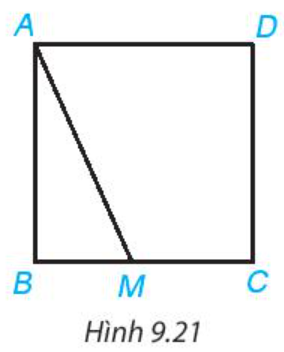
Lời giải:
Nếu M trùng với B hoặc D thì độ dài AM chính là độ dài hình cạnh hình vuông ABCD (1)
Mặt khác, nếu M không trùng với B và D thì AM là đường xiên kẻ từ A xuống BC hoặc CD.
Mà đường xiên bao giờ cũng lớn hơn đường vuông góc
Do đó, AM lớn hơn độ dài cạnh hình vuông (2)
Từ (1) và (2) suy ra, độ dài đoạn thẳng AM luôn lớn hơn hoặc bằng độ dài cạnh của hình vuông đó (M di chuyển trên trên cạnh BC hoặc DC).
Bài 9.15 trang 71 Toán 7 Tập 2:
Hỏi có tam giác nào với độ dài ba cạnh là 2,5 cm; 3,4 cm và 6 cm không? Vì sao?
Lời giải:
Ta có 2,5 + 3,4 = 5,9 < 6, độ dài ba đoạn thẳng 2,5 cm; 3,4 cm và 6 cm không thỏa mãn một bất đẳng thức tam giác nên không phải độ dài ba cạnh của một tam giác.
Do đó không có tam giác nào có độ dài ba cạnh là 2,5 cm; 3,4 cm và 6 cm.
Bài 9.16 trang 71 Toán 7 Tập 2:
Tính chu vi của tam giác cân biết hai cạnh của nó có độ dài là 2 cm và 5 cm.
Lời giải:
Do tam giác đã cho là tam giác cân nên độ dài cạnh đáy có thể là 2 cm hoặc 5 cm.
Khi đó, ta xét hai trường hợp sau:
• Trường hợp 1: bộ ba cạnh của tam giác có độ dài là 2 cm; 2 cm; 5 cm.
Ta thấy 2 + 2 = 4 < 5 nên bộ ba độ dài này không tạo thành một tam giác.
• Trường hợp 2: bộ ba cạnh của tam giác có độ dài là 5 cm, 5 cm, 2 cm.
Ta thấy 5 + 2 = 7 > 5 nên bộ ba độ dài này tạo thành một tam giác với độ dài cạnh đáy là 2 cm và hai cạnh bên có độ dài là 5 cm.
Khi đó chu vi tam giác đó là: 5 + 5 + 2 = 12 (cm).
Vậy chu vi của tam giác cân đã cho là 12 cm.
Bài 9.17 trang 71 Toán 7 Tập 2:
Độ dài hai cạnh của một tam giác bằng 7 cm và 2 cm. Tính độ dài cạnh còn lại biết rằng số đo của nó theo xentimét là một số tự nhiên lẻ.
Lời giải:
Gọi độ dài cạnh còn lại của tam giác là x (cm).
Áp dụng bất đẳng thức tam giác ta có:
7 – 2 < x < 7 + 2 hay 5 < x < 9.
Mà x là một số tự nhiên lẻ nên x = 7.
Vậy độ dài cạnh còn lại của tam giác bằng 7 cm.
Bài 9.18 trang 71 Toán 7 Tập 2:
Biết hai cạnh của tam giác có độ dài a và b. Dựa vào bất đẳng thức tam giác, hãy giải thích tại sao chu vi của tam giác đó lớn hơn 2a và nhỏ hơn 2(a + b).
Lời giải:
Gọi độ dài cạnh còn lại của tam giác là c (cm) (c > 0).
Áp dụng bất đẳng thức tam giác ta có: c < a + b và a < b + c.
Do c < a + b nên (a + b) + c < (a + b) + (a + b) hay a + b + c < 2(a + b) (1)
Do a < b + c nên a + a < a + (b + c) hay 2a < a + b + c (2)
Từ (1) và (2) suy ra 2a < a + b + c < 2(a + b).
Mà chu vi của tam giác là a + b + c (cm).
Vậy chu vi của tam giác đó lớn hơn 2a và nhỏ hơn 2(a + b).
Bài 9.19 trang 71 Toán 7 Tập 2:
Hai khu vườn A và B nằm về một phía của con kênh d. Hãy xác định bên bờ kênh cùng phía với A và B, một điểm C để đặt máy bơm nước từ kênh tưới cho hai khu vườn sao cho tổng độ dài đường ống dẫn nước từ máy bơm đến hai khu vườn là ngắn nhất (HD: Gọi B’ là điểm sao cho d là đường trung trực của BB’ (H.9.22). Khi đó CB = CB’. Xem Vận dụng, Bài 33).
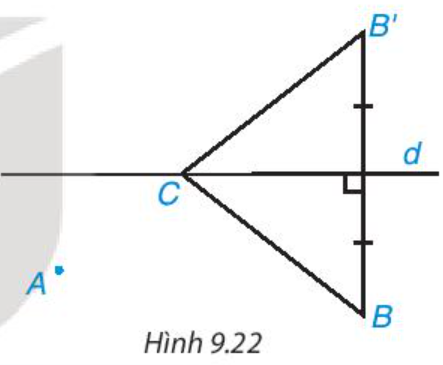
Lời giải:
Gọi B’ là điểm sao cho d là đường trung trực của đoạn thẳng BB’.
Vì C nằm trên đường trung trực của BB’ nên C cách đều hai đầu mút B và B’.
Do đó CB = CB’.
Ta có: Độ dài đường ống dây dẫn nước từ máy bơm đến hai khu vườn là AC + CB.
Mà CB = CB’ nên AC + BC = AC + CB’.
Ta có thể thấy để AC + CB’ nhỏ nhất khi A, C, B’ thẳng hàng.
Vậy C là giao điểm của d và AB’ với B’ là điểm sao cho d là đường trung trực của BB’.
Xem thêm các bài giải sách giáo khoa Toán 7 bộ sách Kết nối tri thức hay, chi tiết khác:
Bài 34: Sự đồng quy của ba đường trung tuyến. Ba đường phân giác trong một tam giác
Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác
Luyện tập chung trang 83
Bài tập cuối chương 9
Bài 1: Tập hợp các số hữu tỉ
Đăng bởi: THCS Bình Chánh
Chuyên mục: Giải Toán 7 Kết nối tri thức
- Giải Bài 9.29 trang 81 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 9.30 trang 81 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.33 trang 21 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.27 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.28 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.29 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống









