Giải Toán 7 Bài 2 Chân trời sáng tạo: Tam giác bằng nhau
Mời các em theo dõi nội dung bài học do thầy cô trường Trung học Bình Chánh biên soạn sẽ giúp các em nắm chắc kiến thức nội dung bài học tốt hơn.
Giải bài tập Toán 7 Bài 2: Tam giác bằng nhau
A. Các câu hỏi trong bài
Bạn đang xem: Giải Toán 7 Bài 2 Chân trời sáng tạo: Tam giác bằng nhau
Giải Toán 7 trang 48 Tập 2
Khởi động trang 48 Toán 7 Tập 2:
Thế nào là hai tam giác bằng nhau?
Lời giải:
Sau khi tìm hiểu Khám phá 1, ta sẽ trả lời được câu hỏi trên như sau:
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
Khám phá 1 trang 48 Toán 7 Tập 2:
Dùng kéo cắt một tờ giấy thành hình tam giác ABC. Đặt tam giác ABC lên tờ giấy thứ hai. Vẽ và cắt theo các cạnh của tam giác ABC thành tam giác A’B’C’ (Hình 1).
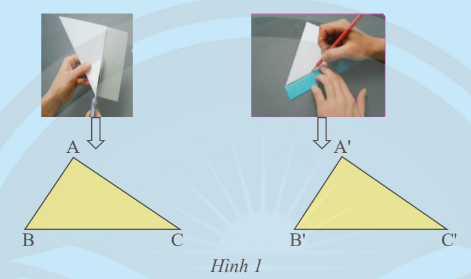
Hãy so sánh các cạnh và các góc của hai tam giác ABC và A’B’C’.
Lời giải:
Thực hiện theo các bước ta được hai tam giác ABC và A’B’C’.
Đo độ dài của các cạnh và số đo của các góc của hai tam giác ABC và A’B’C’ (sử dụng thước thẳng có vạch chia và thước đo góc) ta được:
AB = A’B’; AC = A’C’; BC = B’C’; ; ; .
Giải Toán 7 trang 49 Tập 2
Thực hành 1 trang 49 Toán 7 Tập 2:
Quan sát Hình 4.
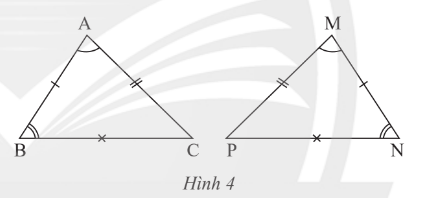
Hai tam giác ABC và MNP có bằng nhau không? Hãy chỉ ra các cặp góc và các cặp cạnh tương ứng bằng nhau.
Lời giải:
Xét ABC có (tổng số đo ba góc của một tam giác).
Suy ra
Xét MNP có (tổng số đo ba góc của một tam giác).
Suy ta
Mà nên .
Do đó ABC = MNP vì có:
• Các cặp cạnh tương ứng bằng nhau là AB = MN, AC = MP, BC = NP.
• Các cặp góc tương ứng bằng nhau là , , .
Vận dụng 1 trang 49 Toán 7 Tập 2:
Trong Hình 5, cho biết ∆GHI = ∆MNP. Hãy tính số đo góc M và độ dài cạnh GI.
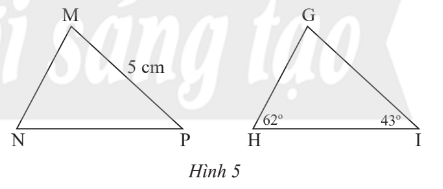
Lời giải:
Xét GIH có (tổng số đo ba góc của một tam giác).
Suy ra .
Do đó = 180° – 62° – 43° = 75° .
Theo bài: ∆GHI = ∆MNP.
Suy ra (hai góc tương ứng) và GI = MP (hai cạnh tương ứng).
Do đó và MP = GI = 5 cm.
Vậy = 75°, GI = 5 cm.
Giải Toán 7 trang 50 Tập 2
Khám phá 2 trang 50 Toán 7 Tập 2:
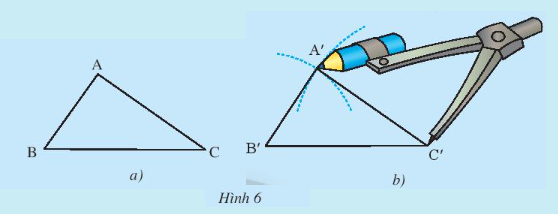
Cho tam giác ABC như trong Hình 6a. Lấy một tờ giấy, trên đó vẽ tam giác A’B’C’ có ba cạnh bằng ba cạnh của tam giác ABC (A’B’ = AB, A’C’ = AC, B’C’ = BC) theo các bước:
– Vẽ đoạn thẳng B’C’ = BC.
– Vẽ cung tròn tâm B’ có bán kính bằng BA, vẽ cung tròn tâm C’ có bán kính bằng CA.
– Hai cung tròn trên cắt nhau tại A’ (chỉ lấy một trong hai giao điểm của hai cung).
– Vẽ các đoạn thẳng B’A’, C’A’ ta được tam giác A’B’C’ (Hình 6b).
Em hãy cắt rời tam giác A’B’C’ ra khỏi tờ giấy vừa vẽ và thử xem có thể đặt chồng khít tam giác A’B’C’ lên tam giác ABC hay không.
Theo em, hai tam giác ABC và A’B’C’ trong trường hợp này có bằng nhau hay không?
Lời giải:
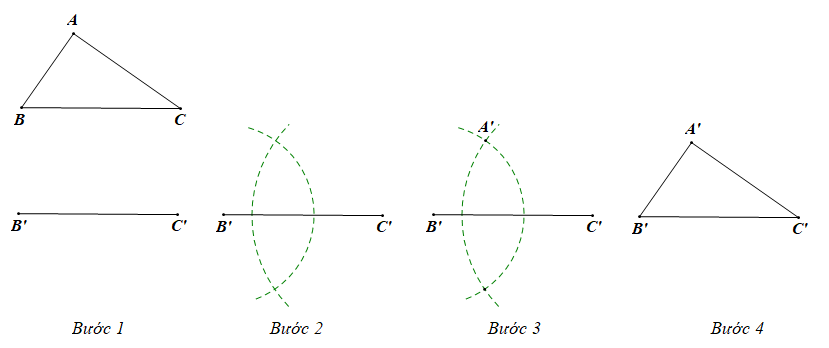
Vẽ tam giác A’B’C’ có ba cạnh bằng ba cạnh của tam giác ABC (A’B’ = AB, A’C’ = AC, B’C’ = BC) theo các bước như sau:
Bước 1: Vẽ đoạn thẳng B’C’ = BC.
Bước 2. Vẽ cung tròn tâm B’ bán kính bằng BA và cung tròn tâm C’ bán kính bằng CA.
Bước 3. Hai cung tròn tâm B’ và tâm C’ cắt nhau tại hai điểm, ta lấy một trong hai điểm, điểm đó là điểm A’.
Bước 4. Vẽ các đoạn thẳng B’A’ và C’A’ ta được tam giác A’B’C’.
Cắt rời tam giác A’B’C’ ra khỏi tờ giấy vừa vẽ và đặt tam giác A’B’C’ lên trên tam giác ABC, ta thấy hai tam giác này chồng khít lên nhau.
Do đó, hai tam giác ABC và A’B’C’ trong trường hợp này bằng nhau.
Giải Toán 7 trang 51 Tập 2
Khám phá 3 trang 51 Toán 7 Tập 2:
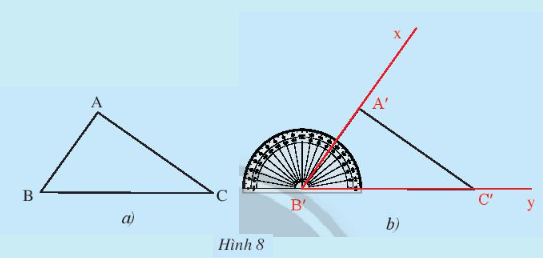
Cho tam giác ABC như trong Hình 8a. Lấy một tờ giấy, trên đó vẽ tam giác A’B’C’ có , B’A’ = BA, B’C’ = BC theo các bước:
– Vẽ .
– Trên tia B’x lấy đoạn B’A’ = BA.
– Trên tia B’y lấy đoạn B’C’ = BC.
– Vẽ đoạn A’C’, ta được tam giác A’B’C’ (Hình 8b).
Em hãy cắt rời tam giác A’B’C’ ra khỏi tờ giấy vừa vẽ và thử xem có thể đặt chồng khít tam giác A’B’C’ lên tam giác ABC hay không.
Theo em, hai tam giác ABC và A’B’C’ trong trường hợp này có bằng nhau hay không?
Lời giải:
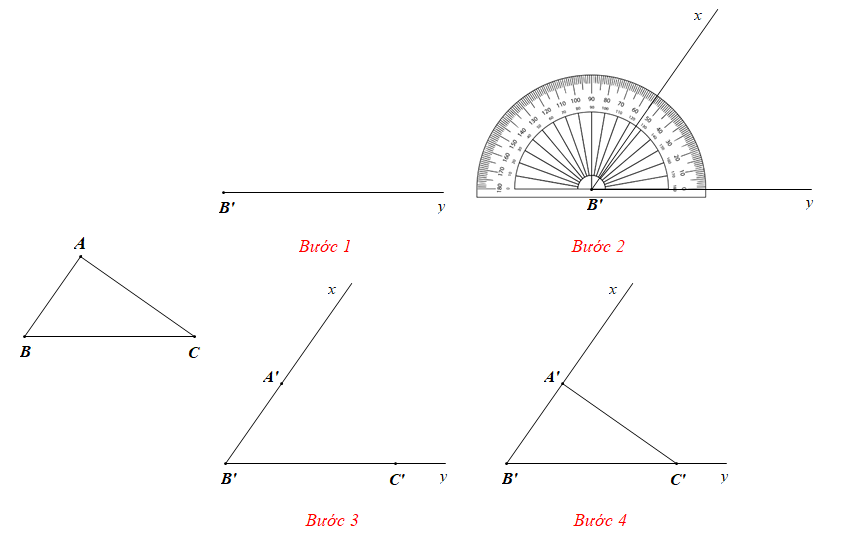
Vẽ tam giác A’B’C’ có , B’A’ = BA, B’C’ = BC theo các bước như sau:
Bước 1: Vẽ tia B’y.
Bước 2: Vẽ tia B’x sao cho .
Bước 3: Trên tia B’x lấy đoạn B’A’ = BA; trên tia B’y lấy đoạn B’C’ = BC.
Bước 4: Vẽ đoạn A’C’ ta được tam giác A’B’C’.
Cắt rời tam giác A’B’C’ ra khỏi tờ giấy và đặt tam giác A’B’C’ lên trên tam giác ABC, ta thấy tam giác A’B’C’ chồng khít tam giác ABC.
Do đó, hai tam giác A’B’C’ và ABC trong trường hợp này bằng nhau.
Giải Toán 7 trang 52 Tập 2
Khám phá 4 trang 52 Toán 7 Tập 2:
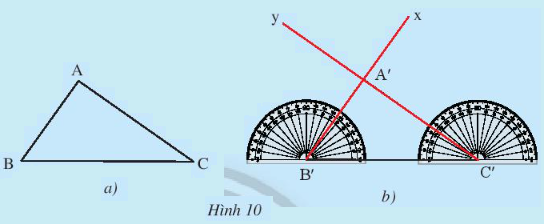
Cho tam giác ABC như trong Hình 10a. Lấy một tờ giấy, trên đó vẽ tam giác A’B’C’ có B’C’ = BC, , theo các bước:
– Vẽ đoạn thẳng B’C’ = BC.
– Ở về cùng một phía của tờ giấy đối với đường thẳng B’C’ vẽ và vẽ .
– Vẽ giao điểm A’ của hai tia B’x và C’y, ta được tam giác A’B’C’ (Hình 10b).
Em hãy cắt rời tam giác A’B’C’ ra khỏi tờ giấy vừa vẽ và thử xem có thể đặt chồng khít tam giác A’B’C’ lên tam giác ABC hay không.
Theo em, hai tam giác ABC và A’B’C’ trong trường hợp này có bằng nhau hay không?
Lời giải:
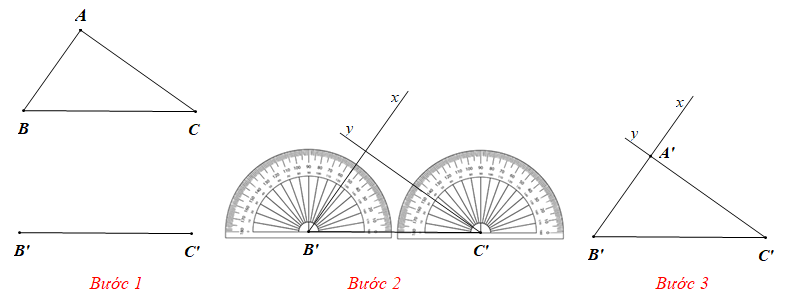
Vẽ tam giác A’B’C’ có B’C’ = BC, , theo các bước như sau:
Bước 1: Vẽ đoạn thẳng B’C’ = BC.
Bước 2: Ở về cùng một phía của tờ giấy đối với đường thẳng B’C’ vẽ và vẽ .
Bước 3: Vẽ giao điểm A’ của hai tia B’x và C’y, ta được tam giác A’B’C’.
Cắt rời tam giác A’B’C’ ra khỏi tờ giấy rồi đặt tam giác A’B’C’ lên trên tam giác ABC, ta thấy hai tam giác này chồng khít lên nhau.
Vậy hai tam giác A’B’C’ và ABC trong trường hợp này bằng nhau.
Giải Toán 7 trang 54 Tập 2
Thực hành 2 trang 54 Toán 7 Tập 2:
Hãy chỉ ra các cặp tam giác bằng nhau trong Hình 13 và cho biết chúng bằng nhau theo trường hợp nào.
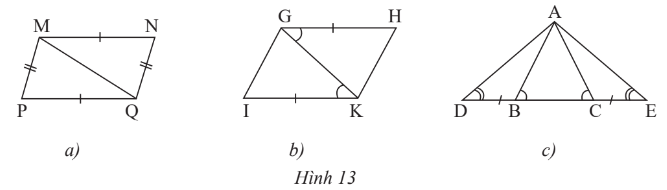
Lời giải:
* Hình 13a:
Xét ∆MQP và ∆QMN có:
PQ = NM (giả thiết);
MP = QN (giả thiết);
Cạnh MQ chung.
Do đó ∆MQP = ∆QMN (c.c.c).
* Hình 13b:
Xét ∆IKG và ∆HGK có:
IK = HG (giả thiết);
(giả thiết);
Cạnh GK chung.
Do đó ∆IKG = ∆HGK (c.g.c).
* Hình 13c:
Trong ∆ABC có nên ∆ABC cân tại A.
Suy ra AB = AC.
Ta có (hai góc kề bù) nên
(hai góc kề bù) nên
Mà nên .
Xét ∆ABD và ∆ACE có:
BD = CE (giả thiết);
(chứng minh trên);
AB = AC (chứng minh trên).
Do đó ∆ABD = ∆ACE (c.g.c).
Mặt khác, có BD = CE nên BD + BC = CE + BC hay DC = EB.
Xét ∆ADC và ∆AEB có:
AC = AB (chứng minh trên);
(giả thiết);
DC = EB (chứng minh trên).
Do đó ∆ADC = ∆AEB (c.g.c).
Thực hành 3 trang 54 Toán 7 Tập 2:
Hai tam giác trong mỗi hình bên (Hình 14a, b) có bằng nhau không? Vì sao?
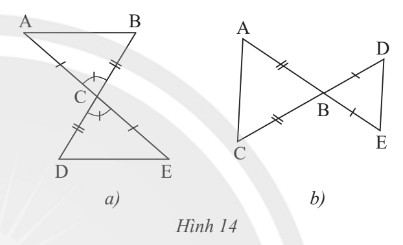
Lời giải:
* Hình 14a:
Xét ∆ABC và ∆EDC có:
BC = DC (giả thiết);
(hai góc đối đỉnh);
AC = EC (giả thiết).
Do đó ∆ABC = ∆EDC (c.g.c).
* Hình 14b:
Không có cạnh nào của tam giác ABC bằng với cạnh của tam giác EBD nên hai tam giác này không bằng nhau.
Vậy Hình 14a có ∆ABC = ∆EDC (c.g.c); Hình 14b hai tam giác ABC và EBC không bằng nhau.
Vận dụng 2 trang 54 Toán 7 Tập 2:
Nêu thêm điều kiện để hai tam giác trong mỗi hình bên (Hình 15a, b) bằng nhau theo trường hợp cạnh – góc – cạnh.
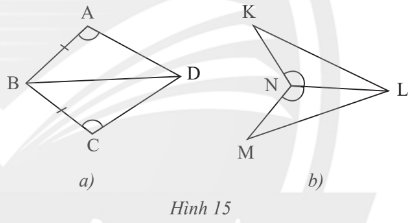
Lời giải:
* Hình 15a:
Xét BAD và BCD có: AB = BC; BD là cạnh chung và .
Trường hợp 1: ta thấy là góc xen giữa hai cạnh AB và AD; là góc xen giữa hai cạnh CB và CD.
Mà và AB = CB.
Do đó để BAD = BCD theo trường hợp cạnh – góc – cạnh thì cần thêm điều kiện về cạnh, đó là AD = CD.
Trường hợp 2: ta thấy là góc xen giữa hai cạnh BA và BD; là góc xen giữa hai cạnh BC và BD.
Mà BA = BC và BD là cạnh chung.
Do đó, để BAD = BCD theo trường hợp cạnh – góc – cạnh thì cần thêm điều kiện về góc, đó là .
* Hình 15b:
Xét KNL và MNL có: cạnh NL chung; = .
Mà là góc xen giữa hai cạnh NK và NL; là góc xen giữa hai cạnh NM và NL.
Do đó, để KNL = MNL theo trường hợp cạnh – góc – cạnh thì cần thêm điều kiện về cạnh, đó là KN = NM.
Vận dụng 3 trang 54 Toán 7 Tập 2:
Cho . Vẽ cung tròn tâm O, cung này cắt Ox, Oy theo thứ tự tại M, N. Vẽ hai cung tròn tâm M và tâm N có cùng bán kính sao cho chúng cắt nhau tại điểm P nằm trong Nối O với P (Hình 16). Hãy chứng minh rằng ∆OMP = ∆ONP, từ đó suy ra OP là tia phân giác của .
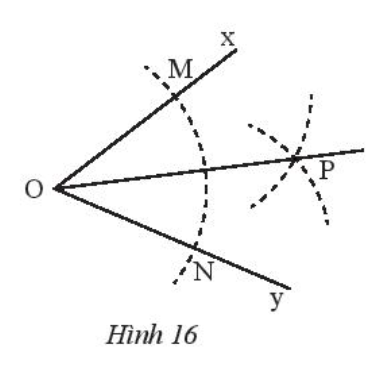
Lời giải:
Do M và N cùng thuộc cung tròn tâm O nên OM = ON.
Hai cung tròn tâm M và N có cùng bán kính, cắt nhau tại P nên MP = NP.
Xét ∆OMP và ∆ONP có:
OM = ON (chứng minh trên);
MP = NP (chứng minh trên);
OP là cạnh chung.
Do đó ∆OMP = ∆ONP (c.c.c).
Suy ra (hai góc tương ứng).
Mà OP nằm giữa hai tia Ox và Oy.
Do đó OP là tia phân giác của .
Giải Toán 7 trang 55 Tập 2
Khám phá 5 trang 55 Toán 7 Tập 2:
Hãy nêu các trường hợp bằng nhau cho mỗi cặp tam giác trong Hình 17.
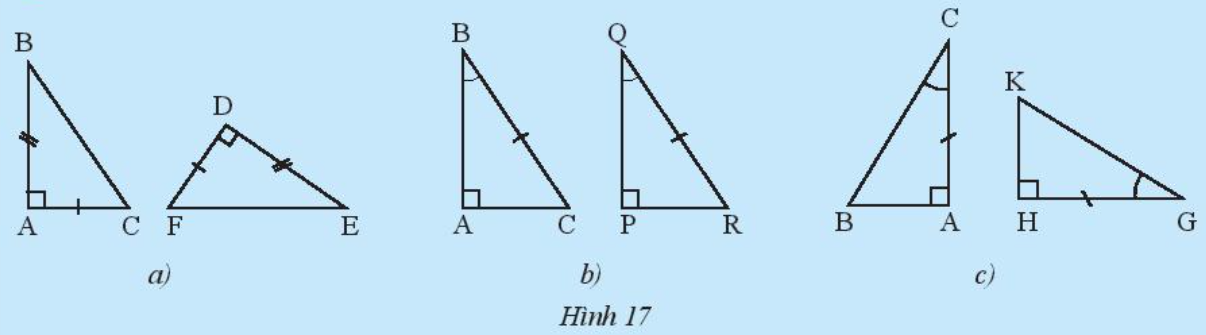
Lời giải:
* Hình 17a:
Xét ∆ABC và ∆DEF có:
AB = DE (giả thiết);
(cùng bằng 90°);
AC = DF (giả thiết).
Do đó ∆ABC = ∆DEF (c.g.c).
* Hình 17b:
Xét ∆ABC vuông tại A có:
= 90o (trong một tam giác vuông, tổng hai góc nhọn bằng 180°)
Suy ra (1).
Xét ∆PQR vuông tại P có:
= 90o (trong một tam giác vuông, tổng hai góc nhọn bằng 180°)
Suy ra (2).
Mà nên từ (1) và (2) ta có .
Xét ∆ABC và ∆PQR có:
(giả thiết);
BC = QR (giả thiết);
(chứng minh trên).
Do đó ∆ABC = ∆PQR (g.c.g).
* Hình 17c:
Xét ∆ABC và ∆HKG có:
(giả thiết);
AC = HG (giả thiết);
(cùng bằng 90°).
Do đó ∆ABC = ∆HKG (g.c.g).
Giải Toán 7 trang 56 Tập 2
Thực hành 4 trang 56 Toán 7 Tập 2:
Tìm các tam giác vuông bằng nhau trong mỗi hình bên (Hình 19).
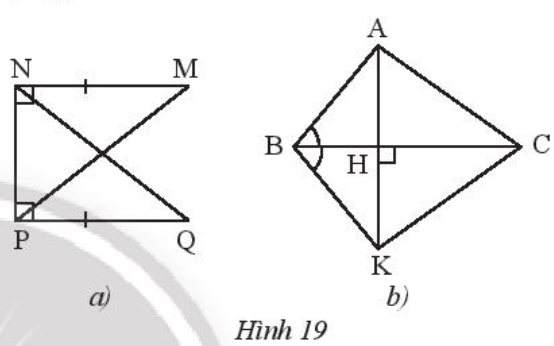
Lời giải:
* Hình 19a:
Xét ∆MNP vuông tại N và ∆QPN vuông tại P có:
MN = QP (giả thiết);
NP là cạnh chung.
Do đó ∆MNP = ∆QPN (hai cạnh góc vuông).
* Hình 19b:
• Xét ∆ABH vuông tại H và ∆KBH vuông tại H có:
(giả thiết);
BH là cạnh chung.
Do đó ∆ABH = ∆KBH (cạnh góc vuông – góc nhọn kề).
Suy ra AH = KH (hai cạnh tương ứng).
• Xét ∆ACH vuông tại H và ∆KCH vuông tại H có:
AH = KH (chứng minh trên);
HC là cạnh chung.
Do đó ∆ACH = ∆KCH (hai cạnh góc vuông).
Khám phá 6 trang 56 Toán 7 Tập 2:
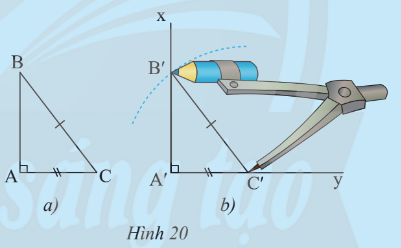
Cho tam giác ABC vuông tại A trong Hình 20a. Vẽ lên tờ giấy tam giác vuông A’B’C’ có cạnh huyền và một cạnh góc vuông bằng với cạnh huyền và một cạnh góc vuông của tam giác ABC như sau:
– Vẽ góc vuông xA’y, trên cạnh A’y vẽ đoạn A’C’ = AC.
– Vẽ cung tròn tâm C’ bán kính bằng BC cắt A’x tại B’.
Cắt rời tam giác A’B’C’. Em hãy cho biết có thể đặt chồng khít tam giác này lên tam giác kia hay không.
Lời giải:
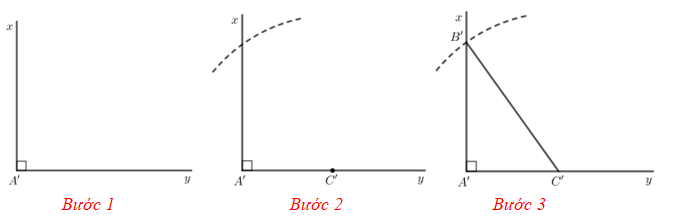
Vẽ ∆A’B’C’ vuông có cạnh huyền và một cạnh góc vuông bằng với cạnh huyền và một cạnh góc vuông của ∆ABC như sau:
Bước 1: Vẽ tia A’y và tia A’x vuông góc với nhau tại điểm A’. Khi đó .
Bước 2: Trên tia A’y lấy điểm C’ sao cho A’C’ = AC. Vẽ cung tròn tâm C’ bán kính bằng BC.
Bước 3: Cung tròn tâm C’ bán kính bằng BC cắt A’x tại điểm B’. Nối B’C’ ta được tam giác A’B’C’.
Cắt rời tam giác A’B’C’ rồi đặt tam giác A’B’C’ lên trên tam giác ABC, ta thấy hai tam giác này đặt chồng khít với nhau.
Giải Toán 7 trang 57 Tập 2
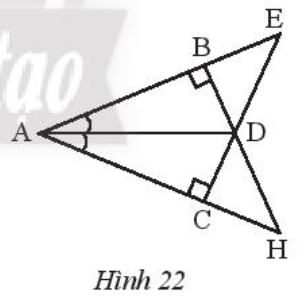
Thực hành 5 trang 57 Toán 7 Tập 2:
Hãy chỉ ra các cặp tam giác bằng nhau trong Hình 22 và cho biết chúng bằng nhau theo trường hợp nào.
Lời giải:
• Xét ∆ABD vuông tại B và ∆ACD vuông tại C có:
AD là cạnh chung;
(giả thiết).
Do đó ∆ABD = ∆ACD (cạnh huyền – góc nhọn).
Suy ra DB = DC (hai cạnh tương ứng).
• Xét ∆DBE vuông tại B và ∆DCH vuông tại C có:
DB = DC (chứng minh trên);
(hai góc đối đỉnh).
Do đó ∆DBE = ∆DCH (cạnh góc vuông – góc nhọn kề).
• Do ∆ABD = ∆ACD (chứng minh trên)
Suy ra AB = AC (hai cạnh tương ứng).
Do ∆DBE = ∆DCH (chứng minh trên)
Suy ra BE = CH (hai cạnh tương ứng).
Do đó AB + BE = AC + CH hay AE = AH.
∙ Xét ∆ADE và ∆ADH có:
AE = AH (chứng minh trên);
(giả thiết);
AD là cạnh chung.
Do đó ∆ADE = ∆ADH (c.g.c).
B. Bài tập
Bài 1 trang 57 Toán 7 Tập 2:
Quan sát Hình 23 rồi thay dấu ? bằng tên tam giác thích hợp.
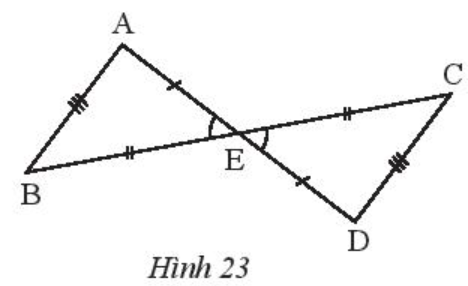
a) ∆ABE = ∆?
b) ∆EAB = ∆?
c) ∆? = ∆CDE.
Lời giải:
Xét ∆ABE và ∆DCE có:
AB = DC, AE = DE, BE = CE (giả thiết)
Suy ra ∆ABE = ∆DCE (c.c.c)
Do đó ∆EAB = ∆EDC (c.c.c) và ∆BAE = ∆CDE (c.c.c).
Vậy ta điền vào như sau:
a) ∆ABE = ∆DCE.
b) ∆EAB = ∆EDC.
c) ∆BAE = ∆CDE.
Bài 2 trang 57 Toán 7 Tập 2:
Cho ∆DEF = ∆HIK và = 73°, DE = 5 cm, IK = 7 cm. Tính số đo và độ dài HI, EF.
Lời giải:
Theo đề bài: ∆DEF = ∆HIK nên:
• (hai góc tương ứng);
• DE = HI (hai cạnh tương ứng);
• EF = IK (hai cạnh tương ứng).
Do đó HI = DE = 5 cm; EF = IK = 7 cm.
Vậy = 73°; HI = 5 cm; EF = 7 cm.
Giải Toán 7 trang 58 Tập 2
Bài 3 trang 58 Toán 7 Tập 2:
Cho hai tam giác bằng nhau ABC và DEF (các đỉnh chưa viết tương ứng), trong đó . Tìm các cặp cạnh bằng nhau, cặp góc tương ứng bằng nhau còn lại.
Lời giải:
Vì hai tam giác ABC và DEF bằng nhau mà và nên đỉnh A tương ứng với đỉnh E, đỉnh C tương ứng với đỉnh D.
Khi đó cặp đỉnh tương ứng còn lại là đỉnh B và đỉnh F hay (hai góc tương ứng).
Do đó hai tam giác này bằng nhau được kí hiệu là ABC = EFD.
Suy ra: AB = EF; BC = FD; CA = DE (các cặp cạnh tương ứng);
Vậy AB = EF; BC = FD; CA = DE và .
Bài 4 trang 58 Toán 7 Tập 2:
Cho biết ∆MNP = ∆DEF và MN = 4 cm, MP = 5 cm, EF = 6 cm. Tìm chu vi tam giác MNP.
Lời giải:
Theo đề bài: ∆MNP = ∆DEF.
Suy ra NP = EF (các cặp cạnh tương ứng).
Mà EF = 6 cm nên NP = 6 cm.
Khi đó, chu vi tam giác MNP là:
MN + MP + NP = 4 + 5 + 6 = 15 (cm).
Vậy chu vi tam giác MNP là 15 cm.
Bài 5 trang 58 Toán 7 Tập 2:
Cho đoạn thẳng AB có O là trung điểm. Vẽ hai đường thẳng m và n lần lượt vuông góc với AB tại A và B. Lấy điểm C trên m, CO cắt n tại D (Hình 24). Chứng minh rằng O là trung điểm của CD.
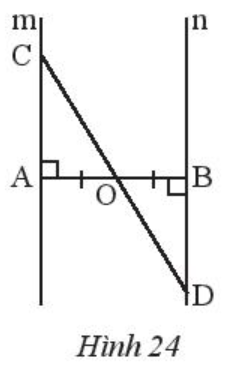
Lời giải:
Xét ∆OAC vuông tại A và ∆OBD vuông tại B có:
OA = OB (giả thiết);
(hai góc đối đỉnh).
Do đó ∆OAC = ∆OBD (cạnh góc vuông – góc nhọn kề).
Suy ra OC = OD (hai cạnh tương ứng).
Mà O nằm giữa C và D nên O là trung điểm của CD.
Vậy O là trung điểm của CD.
Bài 6 trang 58 Toán 7 Tập 2:
Cho Hình 25 có EF = HG, EG = HF. Chứng minh rằng:
a) ∆EFH = ∆HGE.
b) EF // HG.
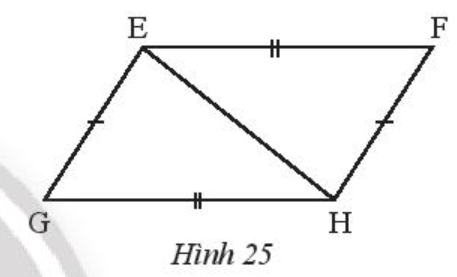
Lời giải:
a) Xét ∆EFH và ∆HGE có:
EF = HG (giả thiết);
EG = HF (giả thiết);
EH là cạnh chung.
Do đó ∆EFH = ∆HGE (c.c.c).
b) Từ câu a: ∆EFH = ∆HGE.
Suy ra (hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên EF // HG.
Vậy EF // HG.
Bài 7 trang 58 Toán 7 Tập 2:
Cho tam giác FGH có FG = FH. Lấy điểm I trên cạnh GH sao cho FI là tia phân giác của . Chứng minh rằng hai tam giác FIG và FIH bằng nhau.
Lời giải:
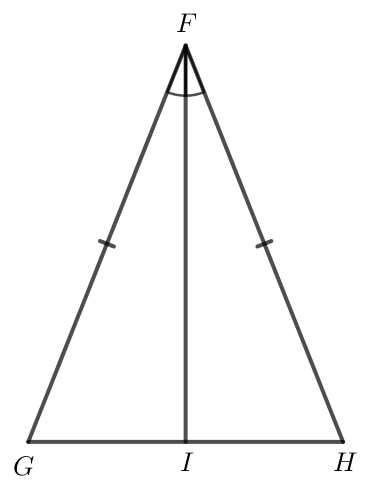
Xét ∆FIG và ∆FIH có:
FG = FH (giả thiết);
(do FI là tia phân giác của );
FI là cạnh chung.
Do đó ∆FIG = ∆FIH (c.g.c).
Bài 8 trang 58 Toán 7 Tập 2:
Cho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng:
a) AD = BC;
b) ∆EAB = ∆ECD;
c) OE là tia phân giác của góc xOy.
Lời giải:
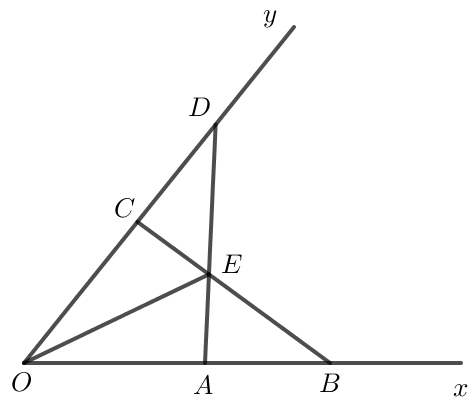
a) Xét ∆OAD và ∆OCB có:
OA = OC (giả thiết);
là góc chung;
OD = OB (giả thiết).
Do đó ∆OAD = ∆OCB (c.g.c).
Suy ra AD = BC (hai cạnh tương ứng).
b) Theo đề bài: OA = OC, OB = OD
Suy ra OB – OA = OD – OC hay AB = CD.
Từ câu a: ∆OAD = ∆OCB.
Suy ra và (các cặp góc tương ứng).
Mặt khác: (hai góc kề bù) và (hai góc kề bù)
Do đó hay .
Xét ∆EAB và ∆ECD có:
(chứng minh trên);
AB = CD (chứng minh trên);
(chứng minh trên).
Do đó ∆EAB = ∆ECD (g.c.g).
c) Từ câu b: ∆EAB = ∆ECD.
Suy ra BE = DE (hai cạnh tương ứng).
Xét ∆ODE và ∆OBE có:
OD = OB (giả thiết);
DE = BE (chứng minh trên);
OE là cạnh chung.
Do đó ∆ODE = ∆OBE (c.c.c).
Suy ra (hai góc tương ứng).
Vậy OE là tia phân giác của .
Bài 9 trang 58 Toán 7 Tập 2:
Đặt tên cho một số điểm có trong Hình 26 và chỉ ra ba cặp tam giác bằng nhau trong hình đó.
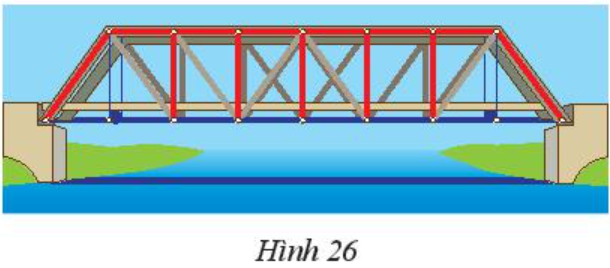
Lời giải:
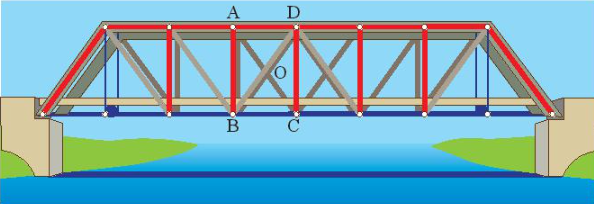
Đặt tên các điểm A, B, C, D, O như hình vẽ trên.
Dựa vào hình trên, ta có ba cặp tam giác bằng nhau như sau:
∆OAB = ∆OCD; ∆ADC = ∆DAB; ∆OAD = ∆OBC.
Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Góc và cạnh của một tam giác
Bài 2: Tam giác bằng nhau
Bài 3: Tam giác cân
Bài 4: Đường vuông góc và đường xiên
Bài 5: Đường trung trực của một đoạn thẳng
Đăng bởi: THCS Bình Chánh
Chuyên mục: Toán 7 Chân trời sáng tạo
- Giải Bài 9.29 trang 81 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 9.30 trang 81 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.33 trang 21 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.27 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.28 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống
- Giải Bài 6.29 trang 20 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống









