Toán 10 Bài 1 Cánh diều: Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây| Giải Toán lớp 10
Mời các em theo dõi nội dung bài học do thầy cô trường Trung học Bình Chánh biên soạn sẽ giúp các em nắm chắc kiến thức nội dung bài học tốt hơn.
Giải bài tập Toán 10 Bài 1: Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây.
A. Các câu hỏi trong bài
Bạn đang xem: Toán 10 Bài 1 Cánh diều: Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây| Giải Toán lớp 10
Giải Toán 10 trang 3 Tập 2
Câu hỏi khởi động trang 3 Toán 10 Tập 2: Sơ đồ ở Hình 1 cho biết lịch thi đấu giải bóng đá UEFA Champions League 2020 – 2021 bắt đầu từ vòng tứ kết.
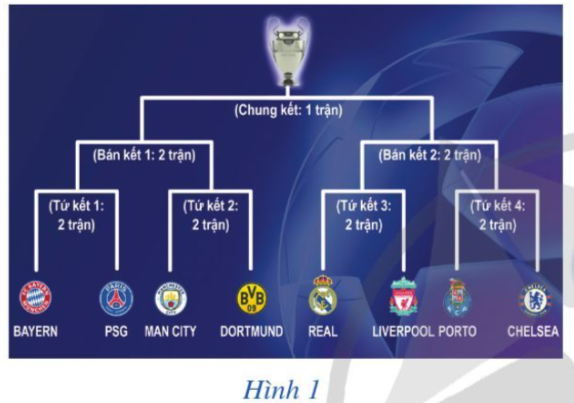
Có bao nhiêu trận đấu của giải bóng đá UEFA Champions League 2020 – 2021 bắt đầu từ vòng tứ kết ?
Lời giải
Theo Hình 1:
– có 4 vòng tứ kết, mỗi vòng có 2 trận đấu nên có 4.2 = 8 trận đấu ở vòng tứ kết;
– có 2 vòng bán kết, mỗi vòng có 2 trận đấu nên có 2.2 = 4 trận đấu ở vòng bán kết;
– có 1 trận đấu ở vòng chung kết.
Vậy có 8 + 4 + 1 = 13 trận đấu đấu của giải bóng đá UEFA Champions League 2020 – 2021 bắt đầu từ vòng tứ kết.
Hoạt động 1 trang 3 Toán 10 Tập 2: Gia đình bạn Liên dự định đi du lịch ở Quy Nhơn (Bình Định). Hướng dẫn viên du lịch đưa ra hai chương trình tham quan như sau:
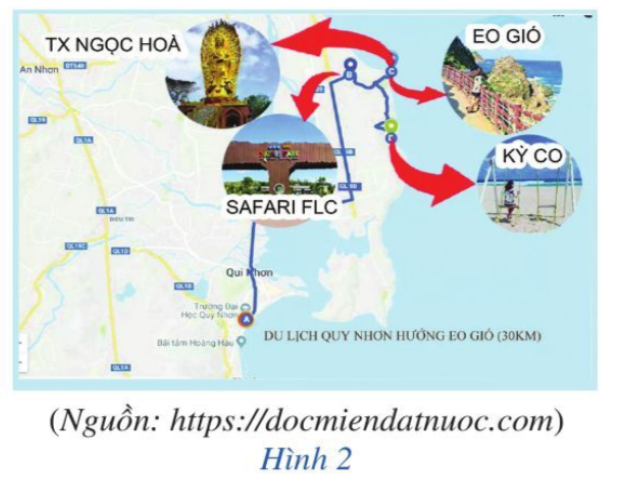
Chương trình 1 có 4 địa điểm tham quan: khu Safari FLC, khu du lịch Eo Gió, khu du lịch Kỳ Co, Tịnh xá Ngọc Hòa (Hình 2).
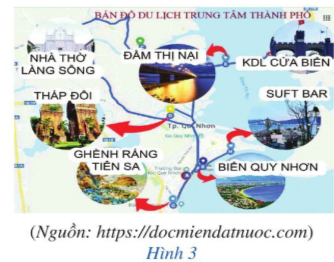
Chương trình 2 có 7 địa điểm tham quan: biển Quy Nhơn, khu du lịch Ghềnh Ráng Tiên Sa, Tháp Đôi, đầm Thị Nại, khu du lịch Cửa Biển, Suft Bar, nhà thờ Làng Sông (Hình 3).
Có bao nhiêu cách chọn một địa điểm tham quan trong số các địa điểm được giới thiệu trong hai chương trình ở trên?
Lời giải
– Chương trình 1 có 4 địa điểm tham quan khác nhau, nên ta có 4 cách chọn địa điểm tham quan (chọn 1 trong 4 địa điểm).
– Chương trình 2 có 7 địa điểm tham quan khác nhau, nên ta có 7 cách chọn địa điểm tham quan (chọn 1 trong 7 địa điểm).
Vì các địa điểm ở chương trình 1 và chương trình 2 là khác nhau.
Vậy có 4 + 7 = 11 cách để chọn một địa điểm tham quan trong số các địa điểm được giới thiệu trong hai chương trình ở trên.
Giải Toán 10 trang 4 Tập 2
Luyện tập 1 trang 4 Toán 10 Tập 2: Một quán bán ba loại đồ uống: trà sữa, nước hoa quả và sinh tố. Có 5 loại trà sữa, 6 loại nước hoa quả và 4 loại sinh tố. Hỏi mỗi khách hàng có bao nhiêu cách chọn một loại đồ uống?
Lời giải
Việc chọn một loại đồ uống là thực hiện một trong ba hành động sau:
– Chọn một loại trà sữa: có 5 cách chọn (vì có 5 loại trà sữa).
– Chọn một loại nước hoa quả: có 6 cách chọn (vì có 6 loại nước hoa quả).
– Chọn một loại sinh tố: có 4 cách chọn (vì có 4 loại sinh tố).
Vậy mỗi khách hàng có 5 + 6 + 4 = 15 cách chọn một loại đồ uống.
Hoạt động 2 trang 4 Toán 10 Tập 2: Gia đình bạn Thảo dự định đi du lịch từ Lào Cai đến Hà Nội bằng một trong hai phương tiện: xe khách hoặc tàu hỏa. Sau đó, từ Hà Nội đi đến Thành phố Hồ Chí Minh bằng một trong ba phương tiện: máy bay, tàu hỏa, xe khách (Hình 4). Hỏi gia đình bạn Thảo có bao nhiêu cách để lựa chọn phương tiện để đi từ Lào Cai đến Thành phố Hồ Chí Minh, qua Hà Nội?

Lời giải
Để chọn một phương tiện để đi từ Lào Cai đến Thành phố Hồ Chí Minh, qua Hà Nội, bạn Thảo phải thực hiện liên tiếp hai hành động:
– Một là, chọn phương tiện đi từ Lào Cai đến Hà Nội: chọn xe khách hoặc tàu hỏa, có 2 cách chọn.
– Hai là, chọn phương tiện đi từ Hà Nội đến Thành phố Hồ Chí Minh: chọn máy bay, hoặc tàu hỏa, hoặc xe khách, có 3 cách chọn.
Vậy ta có các loại phương tiện có thể cho chuyến đi có các kết quả sau:
+) Xe khách; Máy bay
+) Xe khách; Tàu hỏa
+) Xe khách; Xe khách
+) Tàu hỏa; Máy bay
+) Tàu hỏa; Tàu hỏa
+) Tàu hỏa; Xe khách.
Vậy số cách chọn phương tiện để đi từ Lào Cai đến Thành phố Hồ Chí Minh, qua Hà Nội là 2.3 = 6 (cách chọn).
Giải Toán 10 trang 6 Tập 2
Luyện tập 2 trang 6 Toán 10 Tập 2: Bạn Nam dự định đặt mật khẩu cho khóa vali là một số gồm ba chữ số được chọn ra từ các chữ số 1, 2, 3, 4. Hỏi bạn Nam có bao nhiêu cách đặt mật khẩu?
Lời giải
Để đặt một mật khẩu gồm ba chữ số từ các chữ số 1, 2, 3, 4, ta thực hiện ba hành động liên tiếp: chọn một chữ số hàng trăm, chọn một chữ số hàng chục và chọn một chữ số hàng đơn vị.
Vì mỗi chữ số được chọn là một trong các chữ số 1, 2, 3, 4 (gồm 4 chữ số) nên:
Chọn một chữ số hàng trăm: Có 4 cách chọn.
Chọn một chữ số hàng chục: Có 4 cách chọn.
Chọn một chữ số hàng đơn vị: Có 4 cách chọn.
Vậy theo quy tắc nhân, có 4 . 4 . 4 = 64 cách đặt mật khẩu.
Hoạt động 3 trang 6 Toán 10 Tập 2: Sơ đồ trong Hình 4 mô tả cách chọn phương tiện đi từ Lào Cai đến Thành phố Hồ Chí Minh của gia đình bạn Thảo có thể vẽ lại như sau (Hình 5):
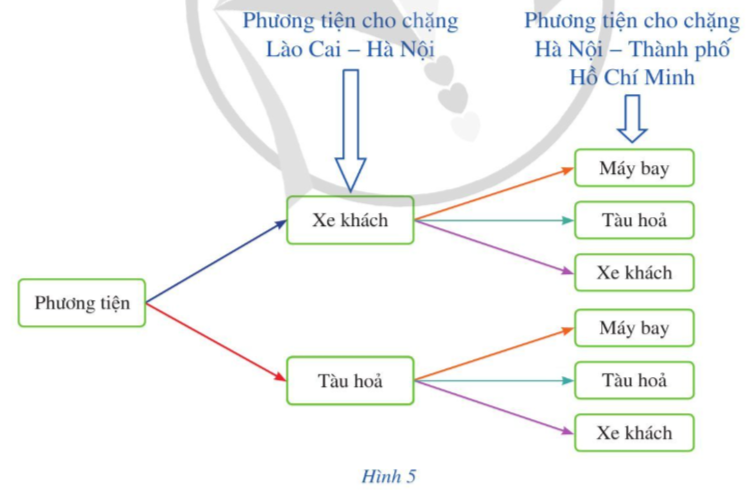
Quan sát sơ đồ hình cây ở Hình 5, cho biết có bao nhiêu cách chọn phương tiện đi từ Lào Cai đến Thành phố Hồ Chí Minh, qua Hà Nội.
Lời giải
Quan sát sơ đồ hình cây ở Hình 5 nhận thấy có hai sự lựa chọn phương tiện cho chặng từ Lào Cai đến Hà Nội (xe khách hoặc tàu hỏa), với mỗi phương tiện loại ở chặng này, ta lại có 3 cách chọn phương tiện cho chặng từ Hà Nội đến Thành phố Hồ Chí Minh (máy bay hoặc tàu hỏa hoặc xe khách).
Vậy có 6 cách chọn phương tiện đi từ Lào Cai đến Thành phố Hồ Chí Minh, qua Hà Nội.
Giải Toán 10 trang 8 Tập 2
Luyện tập 3 trang 8 Toán 10 Tập 2: Từ các chữ số 1, 2, 3, 4, 5, lập được bao nhiêu số lẻ gồm ba chữ số đôi một khác nhau?
Lời giải
Lập một số lẻ gồm ba chữ số đôi một khác nhau từ các chữ số 1, 2, 3, 4, 5 là thực hiện ba hành động liên tiếp: chọn chữ số hàng đơn vị, chọn chữ số hàng chục và chọn chữ số hàng trăm.
– Chọn chữ số hàng đơn vị, do ta cần chọn chữ số hàng đơn vị là số lẻ nên chọn chữ số lẻ 1, hoặc 3, hoặc 5 nên có 3 cách chọn.
– Chọn chữ số hàng chục, do các số được lập gồm 3 chữ số đôi một khác nhau nên chữ số hàng chục được chọn phải khác chữ số hàng đơn vị, vậy chọn 1 chữ số từ 1, 2, 3, 4, 5, trừ đi chữ số hàng đơn vị, có 4 cách chọn.
– Chọn chữ số hàng trăm, tương tự chữ số hàng chục, có 3 cách chọn.
Vậy theo quy tắc nhân, có 3 . 4 . 3 = 36 số lẻ gồm ba chữ số đôi một khác nhau được lập từ các chữ số 1, 2, 3, 4, 5.
B. Bài tập
Giải Toán 10 trang 10 Tập 2
Bài 1 trang 10 Toán 10 Tập 2: Từ các chữ số 1, 2, 3, 4, 5, 6, ta lập ra số tự nhiên gồm ba chữ số, chia hết cho 5. Có thể lập được bao nhiêu số như thế?
Lời giải
Theo dấu hiệu chia hết cho 5, ta có số tự nhiên chia hết cho 5 là số có chữ số tận cùng là 0 hoặc 5. Trong các chữ số đã cho, chỉ có chữ số 5 thỏa mãn ở vị trí chữ số tận cùng của số cần lập.
Việc lập được số thỏa mãn yêu cầu đề bài là việc thực hiện ba hành động liên tiếp: chọn chữ số hàng đơn vị, chọn chữ số hàng chục và chọn chữ số hàng trăm.
– Chọn chữ số hàng đơn vị, ta chọn chữ số 5, có 1 cách chọn.
– Chọn chữ số hàng chục, từ 6 chữ số đã cho, có 6 cách chọn.
– Chọn chữ số hàng trăm, từ 6 chữ số đã cho, có 6 cách chọn.
Vậy theo quy tắc nhân, có thể lập được 1 . 6 . 6 = 36 số tự nhiên thỏa mãn yêu cầu đề bài.
Bài 2 trang 10 Toán 10 Tập 2: Từ các chữ số 1, 2, 3, 4, 5, 6, 7, lập được bao nhiêu số chẵn:
a) Gồm ba chữ số?
b) Gồm ba chữ số đôi một khác nhau?
Lời giải
Một số là số chẵn khi có chữ số tận cùng là 0, 2, 4, 6, 8. Tromg các chữ số đã cho, chỉ có các chữ số 2, 4, 6 thỏa mãn ở vị trí chữ số tận cùng của số cần lập.
a)
Việc lập số chẵn gồm ba chữ số là việc thực hiện ba hành động liên tiếp: chọn chữ số hàng đơn vị, chọn chữ số hàng chục và chọn chữ số hàng trăm.
– Chọn chữ số hàng đơn vị, chọn một trong ba chữ số chẵn 2, 4, 6; có 3 cách chọn.
– Chọn chữ số hàng chục, từ 7 chữ số đã cho, có 7 cách chọn.
– Chọn chữ số hàng trăm, từ 7 chữ số đã cho, có 7 cách chọn.
Vậy theo quy tắc nhân, có 3 . 7 . 7 = 147 số thỏa mãn yêu cầu bài ra.
b)
Việc lập số chẵn gồm ba chữ số đôi một khác nhau là việc thực hiện ba hành động liên tiếp: chọn chữ số hàng đơn vị, chọn chữ số hàng chục và chọn chữ số hàng trăm.
– Chọn chữ số hàng đơn vị, chọn một trong ba chữ số chẵn 2, 4, 6; có 3 cách chọn.
– Chọn chữ số hàng chục, vì số cần lập gồm 3 chữ số đôi một khác nhau nên ta chọn chữ số hàng chục cần khác chữ số hàng đơn vị, nên có 6 cách chọn.
+ Chọn chữ số hàng trăm, tương tự chữ số hàng chục, có 5 cách chọn.
Vậy theo quy tắc nhân, có 3 . 6 . 5 = 90 số thỏa mãn yêu cầu bài ra.
Bài 3 trang 10 Toán 10 Tập 2: Trong một trường trung học phổ thông, khối 10 có 245 học sinh nam và 235 học sinh nữ.
a) Nhà trường cần chọn một học sinh ở khối 10 đi dự buổi giao lưu với học sinh các trường trung học phổ thông trong tỉnh. Hỏi nhà trường có bao nhiêu cách chọn?
b) Nhà trường cần chọn hai học sinh ở khối 10, trong đó có 1 nam và 1 nữ, đi dự trại hè của học sinh trong tỉnh. Hỏi nhà trường có bao nhiêu cách chọn?
Lời giải
a) Việc chọn một học sinh ở khối 10 đi dự buổi giao lưu với học sinh các trường trung học phổ thông trong tỉnh là việc thực hiện một trong hai hành động sau:
– Chọn một học sinh nam: Có 245 cách chọn.
– Chọn một học sinh nữ: Có 235 cách chọn.
Vậy theo quy tắc cộng, nhà trường có 245 + 235 = 480 cách chọn một học sinh.
b) Việc chọn hai học sinh, trong đó có 1 nam và 1 nữ đi dự trại hè của học sinh trong tỉnh là việc thực hiện hai hành động liên tiếp: chọn một học sinh nam và chọn một học sinh nữ.
– Chọn một học sinh nam: Có 245 cách chọn.
– Chọn một học sinh nữ: Có 235 cách chọn
Vậy theo quy tắc nhân, nhà trường có 245 . 235 = 57 575 cách chọn hai học sinh trong đó có 1 nam và 1 nữ.
Bài 4 trang 10 Toán 10 Tập 2: Trong giải thi đấu bóng đá World Cup, vòng bảng có 32 đội tham gia, được chia làm 8 bảng, mỗi bảng có 4 đội đấu vòng tròn một lượt. Tính số trận được thi đấu trong vòng bảng theo thể thức trên.
Lời giải
Để tính số trận thi đấu trong vòng bảng, trước tiên, ta tính số trận thi đấu trong mỗi bảng.
Trong một bảng có 4 đội đấu vòng tròn một lượt, tức mỗi đội đều đá với ba đội còn lại.
Chẳng hạn, có 4 đội thi đấu là Đ1, Đ2, Đ3 và Đ4.
– Đội Đ1 thi đấu với 3 đội còn lại, có 3 trận đấu.
– Đội Đ2 thi đấu với 2 đội còn lại (vì ta đã tính Đ2 đấu với Đ1 ở trên nên Đ2 còn phải đấu với 2 đội Đ3 và Đ4), có 2 trận đấu.
– Đội Đ3 thi đấu với đội Đ4, có 1 trận đấu.
– Đội Đ4 đều tham gia thi đấu với 3 đội trên rồi.
Vậy theo quy tắc cộng, ở mỗi bảng có 3 + 2 + 1 = 6 (trận đấu).
Mà trong giải đấu, có tất cả là 8 bảng nên tổng số trận được thi đấu trong vòng bảng là: 6.8 = 48 (trận).
Vậy có 48 trận được thi đấu ở vòng bảng trong giải thi đấu bóng đá World Cup theo thể thức trên.
Bài 5 trang 10 Toán 10 Tập 2: Ở Canada, mã bưu chính có 6 kí tự gồm: 3 chữ cái in hoa (trong số 26 chữ cái tiếng Anh) và 3 chữ số. Mỗi mã bưu chính bắt đầu bằng 1 chữ cái và xen kẽ bằng 1 chữ số.
(Nguồn: https://capath.vn/postal-code-canada)
a) Có thể tạo được bao nhiêu mã bưu chính?
b) Có thể tạo được bao nhiêu mã bắt đầu bằng chữ S?
c) Có thể tạo được bao nhiêu mã bắt đầu bằng chữ S và kết thúc bằng chữ số 8?
Lời giải
Có 26 chữ cái tiếng Anh, nên chọn một chữ cái tiếng Anh thì có 26 cách chọn.
Có 10 chữ số từ 0 đến 9 nên chọn một chữ số thì có 10 cách chọn.
a)
Vì mỗi mã bưu chính gồm 6 kí tự, bắt đầu bằng một chữ cái và xen kẽ bằng một chữ số nên để tạo một mã bưu chính, ta thực hiện sáu hành động liên tiếp: chọn chữ cái đầu tiên, chọn chữ số thứ hai, chọn chữ cái thứ ba, chọn chữ số thứ tư, chọn chữ cái thứ năm và chọn chữ số thứ sáu.
– Chọn chữ cái đầu tiên: có 26 cách chọn.
– Chọn chữ số thứ hai: có 10 cách chọn.
– Chọn chữ cái thứ ba: có 26 cách chọn.
– Chọn chữ số thứ tư: có 10 cách chọn.
– Chọn chữ cái thứ năm: có 26 cách chọn.
– Chọn chữ số thứ sáu: có 10 cách chọn.
Vậy theo quy tắc nhân, có thể tạo được 26 . 10 . 26 . 10 . 26 . 10 = 17 576 000 mã bưu chính.
b)
Để tạo một mã bưu chính bắt đầu bằng chữ S, ta thực hiện sáu hành động liên tiếp: chọn chữ cái đầu tiên là S, chọn chữ số thứ hai, chọn chữ cái thứ ba, chọn chữ số thứ tư, chọn chữ cái thứ năm và chọn chữ số thứ sáu.
– Chọn chữ cái đầu tiên là chữ cái S: có 1 cách chọn.
– Chọn chữ số thứ hai: có 10 cách chọn.
– Chọn chữ cái thứ ba: có 26 cách chọn.
– Chọn chữ số thứ tư: có 10 cách chọn.
– Chọn chữ cái thứ năm: có 26 cách chọn.
– Chọn chữ số thứ sáu: có 10 cách chọn.
Vậy theo quy tắc nhân, có thể tạo được 1 . 10 . 26 . 10 . 26 . 10 = 676 000 mã bắt đầu bằng chữ S.
c)
Để tạo một mã bưu chính bắt đầu bằng chữ S và kết thúc bằng chữ số 8, ta thực hiện sáu hành động liên tiếp: chọn chữ cái đầu tiên là S, chọn chữ số thứ hai, chọn chữ cái thứ ba, chọn chữ số thứ tư, chọn chữ cái thứ năm và chọn chữ số thứ sáu là chữ số 8.
– Chọn chữ cái đầu tiên là chữ cái S: có 1 cách chọn.
– Chọn chữ số thứ hai: có 10 cách chọn.
– Chọn chữ cái thứ ba: có 26 cách chọn.
– Chọn chữ số thứ tư: có 10 cách chọn.
– Chọn chữ cái thứ năm: có 26 cách chọn.
– Chọn chữ số thứ sáu (chữ số kết thúc) là chữ số 8: có 1 cách chọn.
Vậy theo quy tắc nhân, có thể tạo được 1 . 10 . 26 . 10 . 26 . 1 = 67 600 mã bắt đầu bằng chữ S và kết thúc bằng chữ số 8.
Bài 6 trang 10 Toán 10 Tập 2: Một hãng thời trang đưa ra một mẫu áo sơ mi mới có ba màu: trắng, xanh, đen. Mỗi loại có các cỡ S, M, L, XL, XXL.
a) Vẽ sơ đồ hình cây biểu thị các loại áo sơ mi với màu và cỡ áo nói trên.
b) Nếu một cửa hàng muốn mua tất cả các loại áo sơ mi (đủ loại màu và đủ loại cỡ áo) và mỗi loại một chiếc để về giới thiệu thì cần mua tất cả bao nhiêu chiếc áo sơ mi?
Lời giải
a)
Một mẫu áo sơ mi có:
– Cỡ áo, gồm 5 loại cỡ: S, M, L, XL, XXL.
– Màu áo, gồm 3 loại màu: trắng, xanh, đen.
Vậy ta vẽ sơ đồ hình cây biểu thị các loại áo sơ mi với màu và cỡ áo:
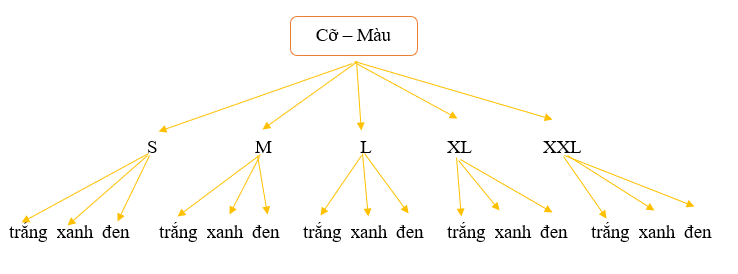
b) Việc mua tất cả các loại áo sơ mi (đủ loại màu và đủ loại cỡ áo) là việc thực hiện hai hành động liên tiếp: chọn cỡ áo và chọn màu áo.
– Chọn cỡ áo: có 5 cách chọn.
– Chọn màu áo: có 3 cách chọn.
Vậy theo quy tắc nhân, cần mua 5 . 3 = 15 chiếc áo sơ mi.
Bài 7 trang 10 Toán 10 Tập 2: Một khách sạn nhỏ chuẩn bị bữa ăn sáng gồm 2 đồ uống là: trà và cà phê; 3 món ăn là: phở, bún và cháo; 2 món tráng miệng là: bánh ngọt và sữa chua.
a) Vẽ sơ đồ hình cây biểu thị các cách chọn khẩu phần ăn gồm đủ ba loại: đồ uống, món ăn và món tráng miệng.
b) Tính số cách chọn khẩu phần ăn gồm: 1 đồ uống, 1 món ăn và 1 món tráng miệng.
Lời giải
a)
Sơ đồ hình cây biểu thị các cách chọn khẩu phần ăn gồm đủ ba loại: món ăn, đồ uống và món tráng miệng:
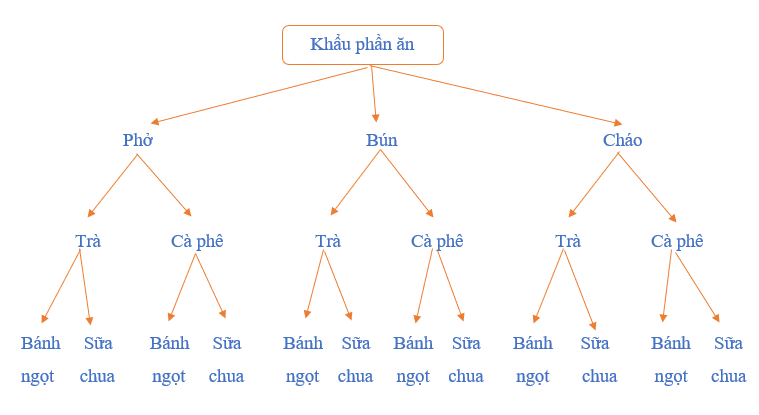
b) Việc chọn khẩu phần ăn là việc thực hiện ba hành động liên tiếp: chọn món ăn, chọn đồ uống và chọn món tráng miệng.
– Chọn món ăn: có 3 cách chọn.
– Chọn đồ uống: có 2 cách chọn.
– Chọn món tráng miệng: có 2 cách chọn.
Vậy theo quy tắc nhân, số cách chọn khẩu phần ăn gồm: 1 đồ uống, 1 món ăn và 1 món tráng miệng là 3 . 2 . 2 = 12 (cách chọn).
Bài 8 trang 10 Toán 10 Tập 2: Cho kiểu gen AaBbDdEe. Giả sử quá trình giảm phân tạo giao tử bình thường, không xảy ra đột biến.
a) Vẽ sơ đồ hình cây biểu thị sự hình thành giao tử.
b) Từ đó, tính số loại giao tử của kiểu gen AaBbDdEe.
Lời giải
a) Sơ đồ hình cây biểu thị sự hình thành giao tử:
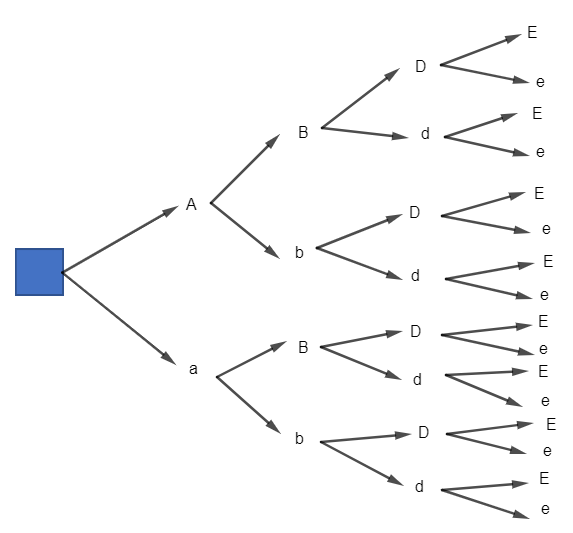
b) Từ sơ đồ hình cây ở câu a, ta thấy số loại giao tử của kiểu gen AaBbDdEe là 16 loại.
Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:
Bài 2: Hoán vị. Chỉnh hợp
Bài 3: Tổ hợp
Bài 4: Nhị thức Newton
Bài tập cuối chương 5
Bài 1: Số gần đúng. Sai số
Đăng bởi: THCS Bình Chánh
Chuyên mục: Toán 10 Cánh Diều
- Giải Bài 4.16 trang 65 Toán 10 tập 1 SGK Kết nối tri thức với cuộc sống
- Giải Bài 1 trang 37 Toán 10 tập 1 SGK Chân trời sáng tạo
- Giải Vận dụng trang 30 Toán 10 tập 1 SGK Kết nối tri thức với cuộc sống
- Triều cường là gì? Triều cường xảy ra khi nào?
- Thơ Đường luật là gì? Đặc điểm của thơ Đường luật
- Phân tích nhân vật he ra clet hay nhất (5 mẫu)









