Khối tứ diện đều có bao nhiêu cạnh?

Nguyễn Thanh Tùng 21/06/2023

Mời các em theo dõi nội dung bài học về Khối tứ diện đều có bao nhiêu cạnh? do thầy cô trường THCS Bình Chánh biên soạn. Hy vọng sẽ là tài liệu hữu ích giúp các em học tốt và hoàn thành tốt bài tập của mình.

Mục lục

Khối tứ diện đều có bao nhiêu cạnh?

Câu hỏi: Khối tứ diện đều có bao nhiêu cạnh?

A. 5

Bạn đang xem: Khối tứ diện đều có bao nhiêu cạnh?

B. 7

C. 8

D. 6

Đáp án đúng: D. 6

Giải thích: Số cạnh của khối tứ diện đều là 6

Số cạnh của khối tứ diện đều là 6 được chứng minh như sau:

Trước tiên, tứ diện là hình có bốn đỉnh, thường được kí hiệu A, B, C, D. Bất kì điểm nào trong số các điểm trên được gọi là đỉnh, mặt tam giác đối diện với đỉnh đó được gọi là đáy. Ví dụ: Chọn A là đỉnh thì (BCD) là mặt đáy.
Trong hình học, một cạnh là một đoạn thẳng nối hai đỉnh trong một đa giác, đa diện, hoặc trong một đa diện chiều cao hơn 3

Nhìn vào hình vẽ minh họa khối tứ diện đều, cùng với 2 khái niệm trên, ta có thể thấy dễ dàng, khối tứ diện đều có 6 cạnh là: AB; AC; AD: BD; DC; CB.

Khối tứ diện đều là một khối đa diện nên nó có đầy đủ những đặc điểm và tính chất của khối đa diện.

Tứ diện là gì?

Tứ diện là hình có bốn đỉnh, được tạo bởi 4 điểm không thẳng hàng trong không gian thường được kí hiệu A, B, C, D. Trong số 4 đỉnh này, bất kì điểm nào trong số các điểm trên được gọi là đỉnh của tứ diện, mặt tam giác đối diện với đỉnh đó được gọi là đáy.

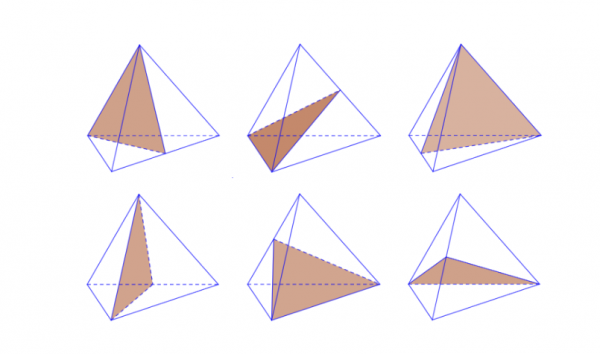
Ví dụ: Chọn A là đỉnh thì mặt đáy sẽ là mặt phẳng được tạo bởi 3 đỉnh còn lại hay mặt phẳng (BCD).

Hay còn hiểu theo một cách gắn gọn khác thì trong không gian nếu cho 4 điểm không đồng phẳng gồm A, B, C, D. Thì khi đó khối đa diện có 4 đỉnh A, B, C, D gọi là khối tứ diện. Và được ký hiệu là ABCD.

Tứ diện đều là gì?

Tứ diện đều được coi là một trong 5 khối đa diện đều. Nếu một hình tứ diện có các mặt bên là các tam giác đều thì đây được gọi là hình tứ diện đều.

Hay ngắn gọn hơn, tứ diện đều là tứ diện có 4 mặt là tam giác đều.

Tứ diện đều là một hình chóp tam giác đều. Như vậy, ta suy ra nếu hình chóp tam giác đều có thêm điều kiện cạnh bên bằng cạnh đáy là tứ diện đều.

Tính chất, cách vẽ và một số công thức liên quan đến tứ diện

Tứ diện đều có các tính chất như sau

Bốn mặt xung quanh là các tam giác đều bằng nhau.
Các mặt của tứ diện là những tam giác có ba góc đều nhọn.
Tổng các góc tại một đỉnh bất kì của tứ diện là 180.
Hai cặp cạnh đối diện trong một tứ diện có độ dài bằng nhau.
Tất cả các mặt của tứ diện đều tương đương nhau.
Bốn đường cao của tứ diện đều có độ dài bằng nhau.
Tâm của các mặt cầu nội tiếp và ngoại tiếp nhau, trùng với tâm của tứ diện.
Hình hộp ngoại tiếp tứ diện là hình hộp chữ nhật.
Các góc phẳng nhị diện ứng với mỗi cặp cạnh đối diện của tứ diện bằng nhau.
Đoạn thẳng nối trung điểm của các cạnh đối diện là một đường thẳng đứng vuông góc của cả hai cạnh đó.
Một tứ diện đều có ba trục đối xứng.
Tổng các cos của các góc phẳng nhị diện chứa cùng một mặt của tứ diện bằng 1.

Cách vẽ tứ diện đều

Để giải bất kỳ bài toán hình học không gian nói chung và bài toán nào liên quan tới hình tứ diện đều nói riêng, bước đầu tiên đều là vẽ hình. Điều quan trọng nhất khi giải bài toán về tứ diện đều là chúng ta phải vẽ chính xác hình tứ diện đều để có một cái hình tổng thể và đưa ra các phương pháp giải chính xác nhất. Sau đây là cách vẽ hình tứ diện đều chi tiết nhất:

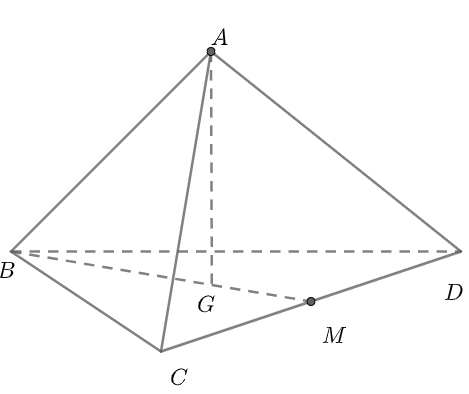
Bước 1: Đầu tiên, coi hình tứ diện đều là môt hình chóp tam giác đều A.BCD (đỉnh A, mặt đáy BCD)
Bước 2: Tiến hành vẽ mặt là cạnh đáy, ở đây ví dụ là mặt BCD.
Bước 3: Xác định trọng tâm G của tam giác BCD. Tiến hành dựng các đường trung trực của cách cạnh đáy của mặt đáy BCD. Ví dụ đường trung tuyến này là BM. Sau đó xác định trọng tâm G là giao của ba đường trung trực của tam giác BCD.
Bước 4: Tiến hành dựng đường cao của tứ diện đều. Đường cao của tứ diện là đường thẳng đi qua đỉnh của tứ diện và vuông góc với mặt đáy. Do tứ diện đều nên đường cao của tứ diện đi qua tâm của mặt đáy BCD. Do đó khi dựng, ta dựng một đường thẳng vuông góc với mặt đáy tại tâm G của tam giác BCD.
Bước 5: Xác định điểm A (đỉnh của tứ diện) trên đường thẳng vừa dựng và nối các đỉnh còn lại với nhau. Ta hoàn thiện được hình tứ diện đều.

Công thức tính thể tích tứ diện

Một tứ diện đều sẽ có 6 cạnh bằng nhau và 4 mặt tam giác đều sẽ có các công thức tính thể tích như sau:

Thể tích tứ diện ABCD: Thể tích của một khối tứ diện bằng một phần ba tích số của diện tích mặt đáy và chiều cao của khối tứ diện tương ứng:

$V = \frac{1}{3}.S_{BCD}.AH$

Thể tích tứ diện đều tam giác S.ABC: Thể tích của một khối chóp bằng một phần ba tích số của diện tích mặt đáy và chiều cao của khối chóp đó: $V = \frac{1}{3}.B.h$

Công thức tính nhanh thể tích tứ diện đều cạnh a

Cho tứ diện đều ABCD cạnh a. từ A kẻ AH là đường cao của hình chóp A.BCD, H thuộc (BCD) thì H sẽ là tâm của tam giác đều BCD. Ta suy ra:

Chiều cao của hình chóp A.BCD đều cạnh a là $h = AH = \frac{a\sqrt{6}}{3}$
Thể tích khối tứ diện đều cạnh a là:

Chứng minh:

Giả sử ABCD là khối tứ diện đều cạnh a. G là trọng tâm tam giác BCD (hình trên). Ta có:

$S_{\Delta BCD} =$ $\frac{a^{2}\sqrt{3}}{4}$

Vậy thể tích khối tứ diện đều cạnh a là:

V = 1/3. S (tam giác BCD) .AG = $\frac{a^{3}\sqrt{2}}{12}$

Câu hỏi trắc nghiệm bổ sung kiến thức về Khối đa diện (Khối tứ diện đều là một trong những khối đa diện)

Câu 1: Trong các mệnh đề sau, mệnh đề nào đúng?

Khối đa diện có các mặt là những tam giác thì:

A. Số mặt và số đỉnh của nó bằng nhau

B. Số mặt và số cạnh của nó bằng nhau

C. Số mặt của nó là một số chẵn

D. Số mặt của nó là một số lẻ

Đáp án: C. Số mặt của nó là một số chẵn

Cách giải:

Cách 1: Ta có thể dùng các phản ví dụ để loại dần các mệnh để sai. Tứ diện (có 4 đỉnh, 4 mặt và 6 cạnh) ta thấy ngay mệnh đề B và D sai.

Từ hình bát diện đều (có 6 đỉnh, 8 mặt) ta thấy mệnh đề A sai.

Vậy C là mệnh đề đúng.

Cách 2: Ta có thể vận dụng công thức (2) ở trên. Thay p = 3 ta có: 3m = 2c.

Vậy m phải là số chẵn.

Câu 2: Trong các mệnh đề sau, mệnh đề nào sai ?

A. Tồn tại một hình đa diện có số cạnh bằng 7

B. Tồn tại một hình đa diện có số cạnh nhỏ hơn 7

C. Số cạnh của một hình đa diện luôn lớn hơn hoặc bằng 6

D. Tồn tại một hình đa diện có số cạnh lớn hơn 7

Đáp án: A. Tồn tại một hình đa diện có số cạnh bằng 7

Cách giải:

Cách 1: Câu C luôn đúng ( theo lí thuyết).

Từ hình tứ diện suy ra câu B đúng.

Từ hình hộp suy ra câu D đúng.

Vậy câu A sai.

Cách 2: Nếu m = 4 thì c = 6. Do đó nếu c = 7 thì m ≥ 5.

Vì mỗi mặt có ít nhất 3 cạnh và mỗi cạnh là cạnh chung của đúng 2 mặt, nên c ≥ (5.3)/2 ≥ 7 vô lí.

Vậy mệnh đề A sai

Câu 3: Trong các mệnh đề sau, mệnh đề nào đúng?

A. Trong một hình đa diện tổng của số mặt và số cạnh nhỏ hơn số đỉnh.

B. Trong một hình đa diện tổng của số mặt và số đỉnh lớn hơn số cạnh

C. Trong một hình đa diện tổng số cạnh và số đỉnh nhỏ hơn số mặt

D. Tồn tại một hình đa diện có tổng của số mặt và số đỉnh nhỏ hơn số cạnh

Đáp án: B. Trong một hình đa diện tổng của số mặt và số đỉnh lớn hơn số cạnh

Cách giải:

Cách 1: Dễ tìm các phản ví dụ để tạo mệnh đề A, C, D

Cách 2: Ta có thể sử dụng công thức Ơle: d + m – 2 = c suy ra B là mệnh đề đúng.

Câu 4: Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất bao nhiêu mặt?

A. 2 mặt

B. 3 mặt

C. 4 mặt

D. 5 mặt

Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất 3 mặt.

Đáp án: B. 3 mặt

Câu 5: Có ít nhất bao nhiêu cạnh xuất phát từ mỗi đỉnh của một hình đa diện?

A. 5 cạnh

B. 4 cạnh

C. 3 cạnh

D. 2 cạnh

Đáp án: C. 3 cạnh

Có ít nhất 3 cạnh xuất phát từ mỗi đỉnh của một hình đa diện.

Câu 6: Hãy tính thể tích khối tứ diện đều ABCD biết:

a) cạnh AB = 4 cm

b) cạnh CD = 6 cm

c) cạnh BD = 3 cm

Hướng dẫn giải

Áp dụng công thức tính thể tích tứ diện đều cạnh a: V = $V = \frac{a^{3}\sqrt{2}}{12}$

a) Vì ABCD là tứ diện đều nên các cạnh có độ dài bằng nhau: BC = CD = DA = BD = AC = AB = 4 cm nên a= 4 (cm). Khi đó thể tích ABCD là: V = 7,54 cm3

b) Vì là tứ diện đều nên AB = BC = DA = BD = AC = CD = 6 cm nên a= 6 (cm). Khi đó thể tích ABCD là: V = 25,46 cm3

c) Vì là tứ diện đều nên AB = BC = CD = DA = AC = BD = 3 cm nên a = 3 (cm). Khi đó thể tích ABCD là: V = 3,18 cm3

Câu 7: Cho hình chóp đều S.ABCD (đáy là hình vuông), đường SA vuông góc với mặt phẳng (ABCD). Xác định hình chóp này có mặt đối xứng nào.

Hướng dẫn giải:

Ta có: BD vuông góc với AC, BD vuông góc với SA.

Từ đó suy ra, BD vuông góc với (SAC) => (SAC) là mặt phẳng trung trực của BD.

Ta kết luận rằng, (SAC) là mặt đối xứng của hình chóp và đây là mặt phẳng duy nhất.

Câu 8: Số mặt phẳng đối xứng của hình tứ diện đều là:

A. 4 mặt phẳng

B. 6 mặt phẳng

C. 8 mặt phẳng

D. 10 mặt phẳng

Câu 9: Trung điểm các cạnh của một tứ diện đều tạo thành:

A. Các đỉnh của một hình hai mươi mặt đều.

B. Các đỉnh của một hình mười hai mặt đều.

C. Các đỉnh của một hình bát diện đều.

D. Các đỉnh của một hình tứ diện.

Câu 10: Cho ABCD là tứ diện đều, cạnh a. Kéo dài BC 1 đoạn CE = a. Kéo dài BD 1 đoạn DF = a. M là trung điểm của AB.

a. Tìm thiết diện của tứ diện với mặt phẳng (MEF).

b. Tính diện tích của thiết diện theo a.

Trên đây là nội dung bài học Khối tứ diện đều có bao nhiêu cạnh? do thầy cô trường THCS Bình Chánh biên soạn và tổng hợp. Hy vọng sẽ giúp các em hiểu rõ nội dung bài học và từ đó hoàn thành tốt bài tập của mình. Đồng thời luôn đạt điểm cao trong các bài thi bài kiểm tra sắp tới. Chúc các em học tập thật tốt.

Đăng bởi THCS Bình Chánh trong chuyện mục Học tập